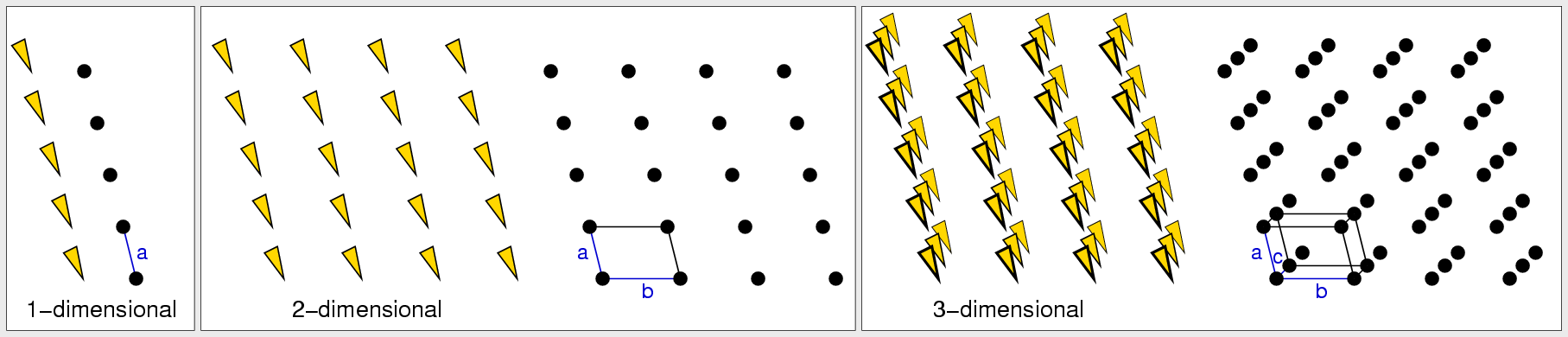
|
| Abb. II.2.1. Translation als Symmetrieoperation ‣ SVG |
| cr_home | Metalle | Nichtmetalle | FK-Chemie | Strukturchemie | Interm. Phasen | Oxide | Silicate | Strukturtypen | AFP |
| ← | Inhalt | Einleitung | I. Spektroskopie | II. Beugung | III. Bildgebung | IV. Sonstige Methoden | → |
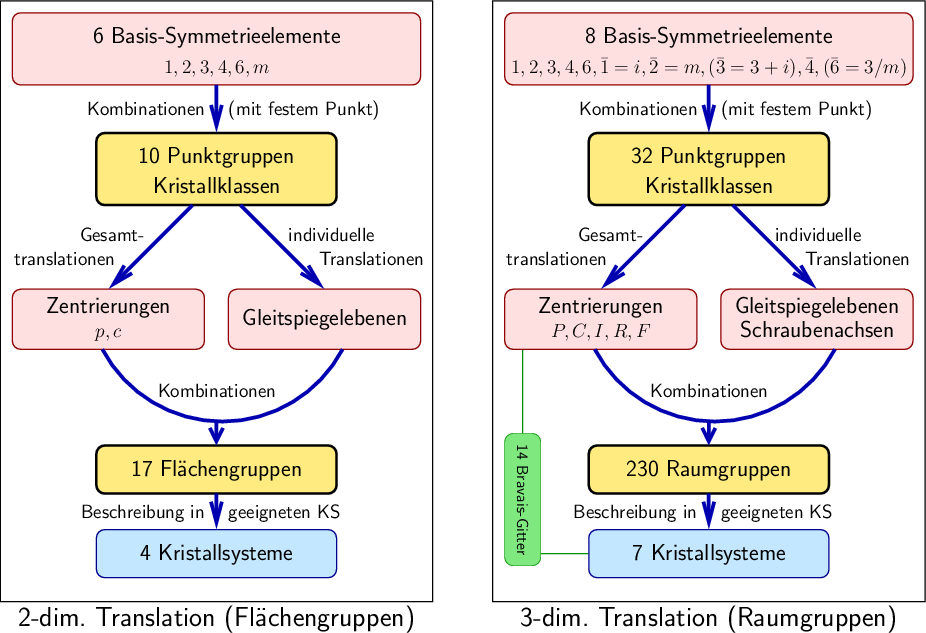
Unterkapitel
Vorlage(n)
| Nr. | Hermann-Mauguin- | Schönflies- | Name | Kristallsystem | |
|---|---|---|---|---|---|
| Kurz-Symbol | Lang-Symbol | Symbol | (Grothe-Bezeichnung) | ||
| 1 | 1 | 1 | C1 | triklin-pedial | triklin (keine ausgezeichnete Richtung): a, b, c beliebig; α, β, γ, beliebig |
| 2 | 1̅ | 1̅ | Ci | triklin-pinakoidal | |
| 3 | m | 1m1 | Cs | monoklin-domatisch | monoklin (eine ausgezeichnete Richtung, die üblicherweise als b-Richtung gewählt wird): a ≠ b, γ beliebig |
| 4 | 2 | 121 | C2 | monoklin-sphenoidisch | |
| 5 | 2/m | 12/m1 | C2h | monoklin-prismatisch | |
| 6 | mm2 | mm2 | C2v | rhombisch pyramidal | orthorhombisch: a ≠ b ≠ c; α=β=γ=90o |
| 7 | 222 | 222 | D2 | rhombisch-dispheniodisch | |
| 8 | mmm | 2/m 2/m 2/m | D2h | rhombisch-dipyramidal | |
| 9 | 4 | 411 | C4 | tetragonal-pyramidal | tetragonal: a=b≠c, α=β=γ=90o |
| 10 | 4̅ | 4̅ | S4 | tetragonal-disphenoidisch | |
| 11 | 4/m | 4/m | C4h | tetragonal-dipyramidal | |
| 12 | 4mm | 4mm | S4 | ditetragonal-pyramidal | |
| 13 | 4̅2m | 4̅2m | C4h | tetragonal-skalenoedrisch | |
| 14 | 422 | 422 | S4 | tetragonal-trapezoedrisch | |
| 15 | 4/mmm | 4/m 2/m 2/m | D4h | ditetragonal-dipyramidal | |
| 16 | 3 | 3 | C3 | trigonal-pyramidal | trigonal, (hexagonale Achsen): a=b≠c, α=β=90o |
| 17 | 3̅ | 3̅ | S6 | rhomboedrisch | |
| 18 | 3m1 | 3m1 | C3v | ditrigonal-pyramidal | |
| 19 | 321 | 321 | D3 | ditrigonal-trapezoedrisch | |
| 20 | 3̅m1 | 3̅ 2/m 1 | D3d | ditrigonal-skalenoedrisch | |
| 21 | 6 | 6 | C6 | hexagonal-pyramidal | hexagonal: a=b≠c; α=β=90o, γ=120o |
| 22 | 6̅ | 6̅ | C3h | trigonal-dipyramidal | |
| 23 | 6/m | 6/m | C6v | hexagonal-dipyramidal | |
| 24 | 6̅m2 | 6̅m2 | D3h | ditrigonal-dipyramidal | |
| 25 | 6mm | 6mm | C6v | dihexagonal-pyramidal | |
| 26 | 622 | 622 | D6 | hexagonal-trapezoedrisch | |
| 27 | 6/mmm | 6/m 2/m 2/m | D6h | dihexagonal-dipyramidal | |
| 28 | 23 | 23 | T | tetraedrisch-pentagondodekaedrisch | kubisch: a=b=c, α=β=γ=90o |
| 29 | m3̅ | 2/m 3̅ | Th | disdodekaedrisch | |
| 30 | 4̅3m | 4̅3m | Td | hexakistetraedrisch | |
| 31 | 432 | 432 | O | pentagonikositetraedrisch | |
| 32 | m3̅m | 4/m 3̅ 2/m | Oh | hexakisoktaedrisch | |

|
| Abb. II.2.1. Translation als Symmetrieoperation ‣ SVG |
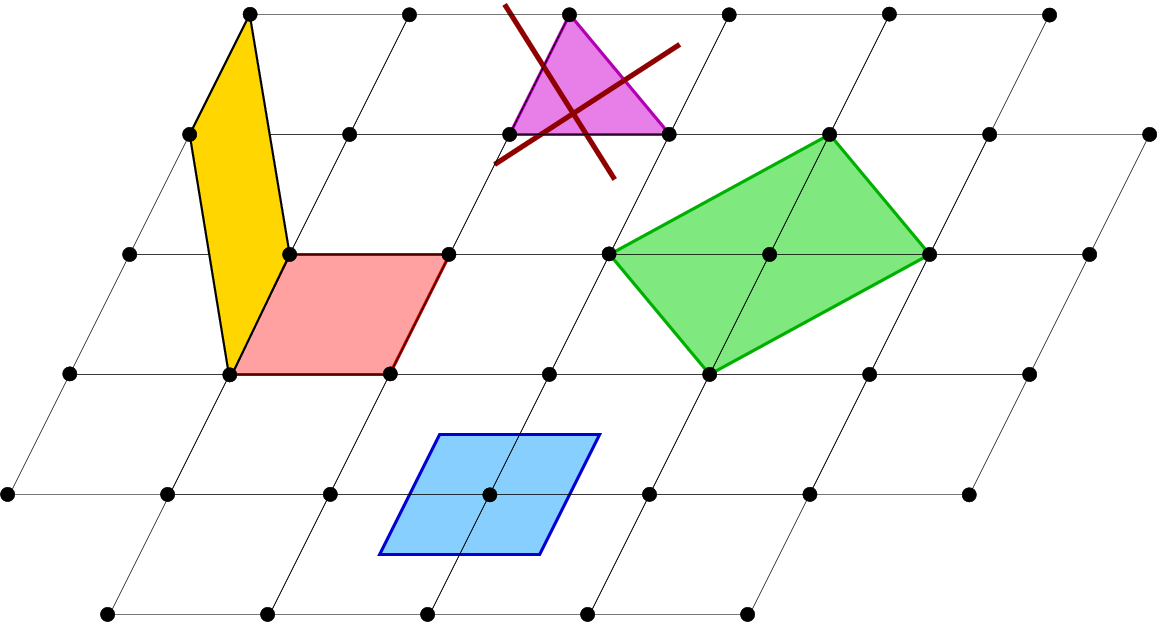
|
| Abb. II.2.2. 2D-Gitter mit verschiedenen Elementarzellen. Die grüne Elementarzelle ist zentriert und enthät zwei Gitterpunkte ‣ SVG |
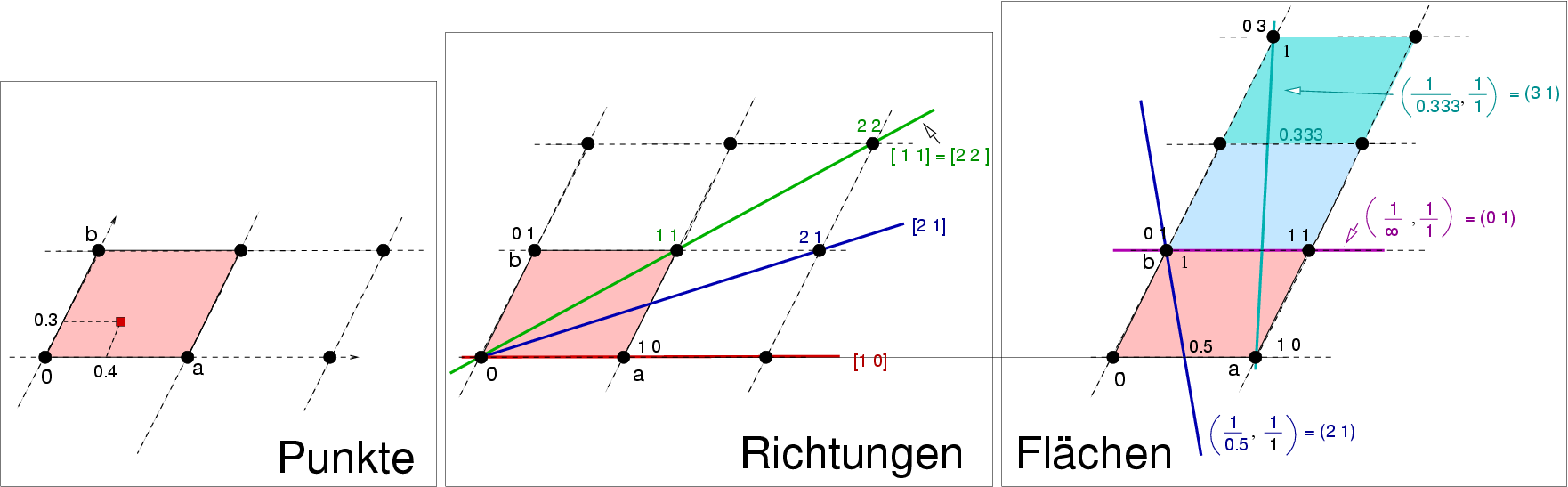
|
| Abb. II.2.3. Punkte, Richtungen (und Flächen) im Zweidimensionalen ‣ SVG |
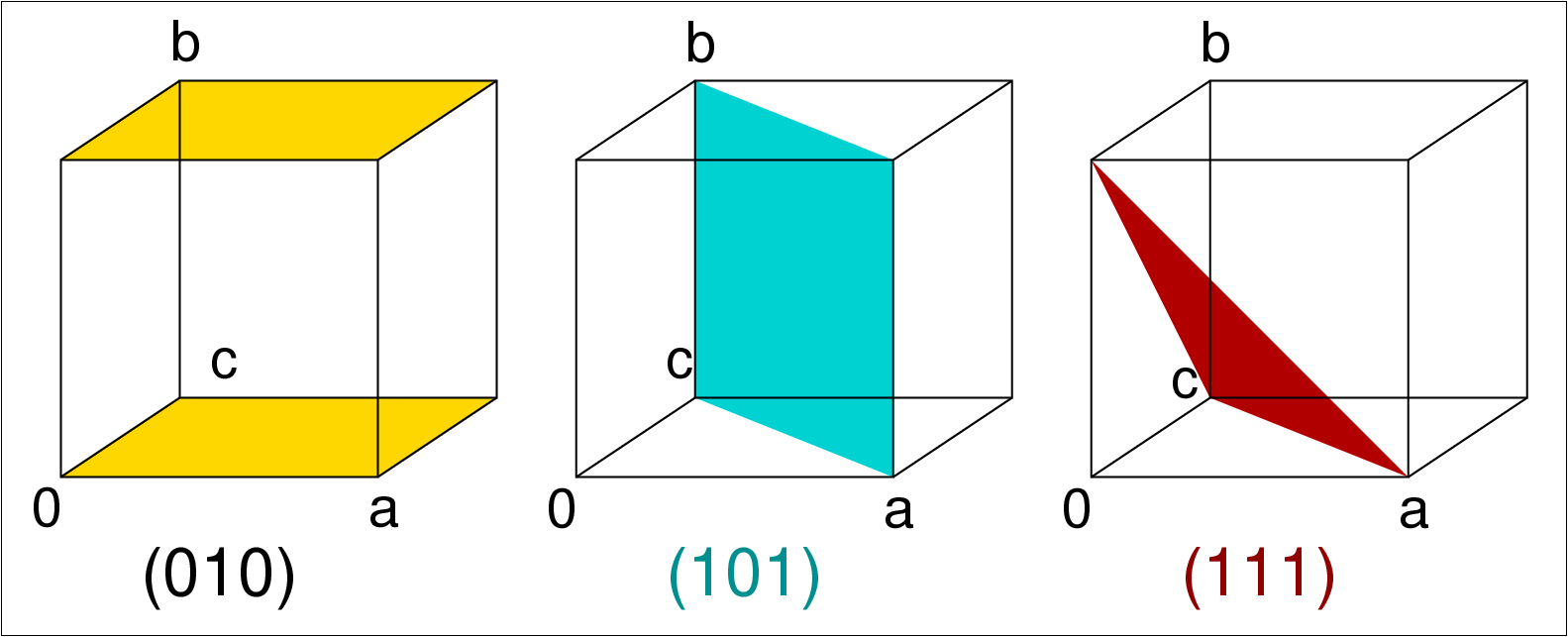
|
| Abb. II.2.4. Ausgezeichnete Flächen im Dreidimensionalen ‣ SVG |

|
| Abb. II.2.5. Drehachsen im 2-dimensionalen (mit Translation vereinbar) ‣ SVG |
|
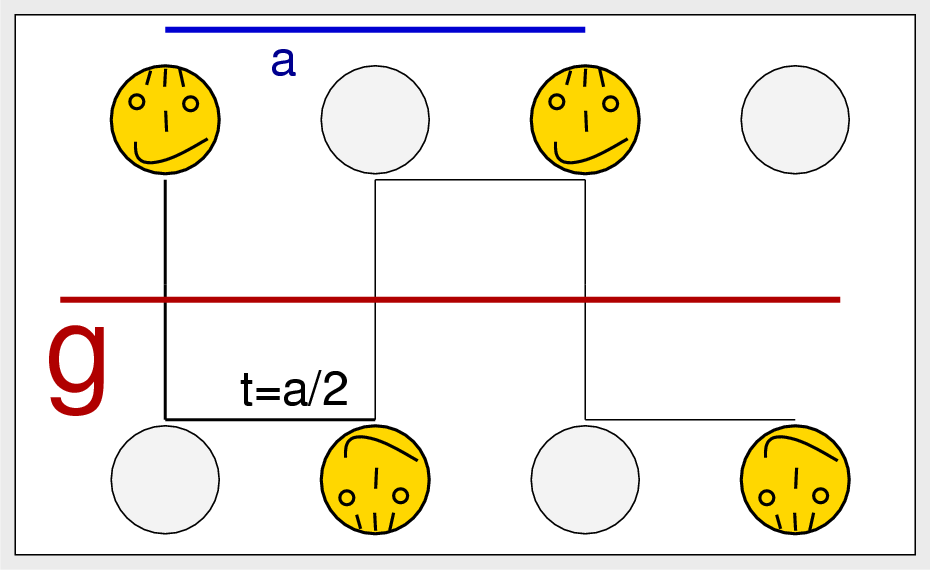
| Abb. II.2.6. Gleitspiegelebene ‣ SVG |
|
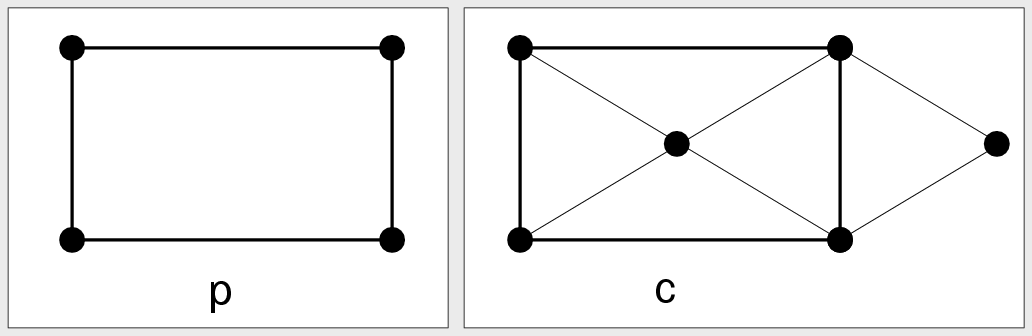
| Abb. II.2.7. Zentrierungen ‣ SVG |
|
| Abb. II.2.8. Flächen- (links) und Raumgruppen (rechts) ‣ SVG |
|
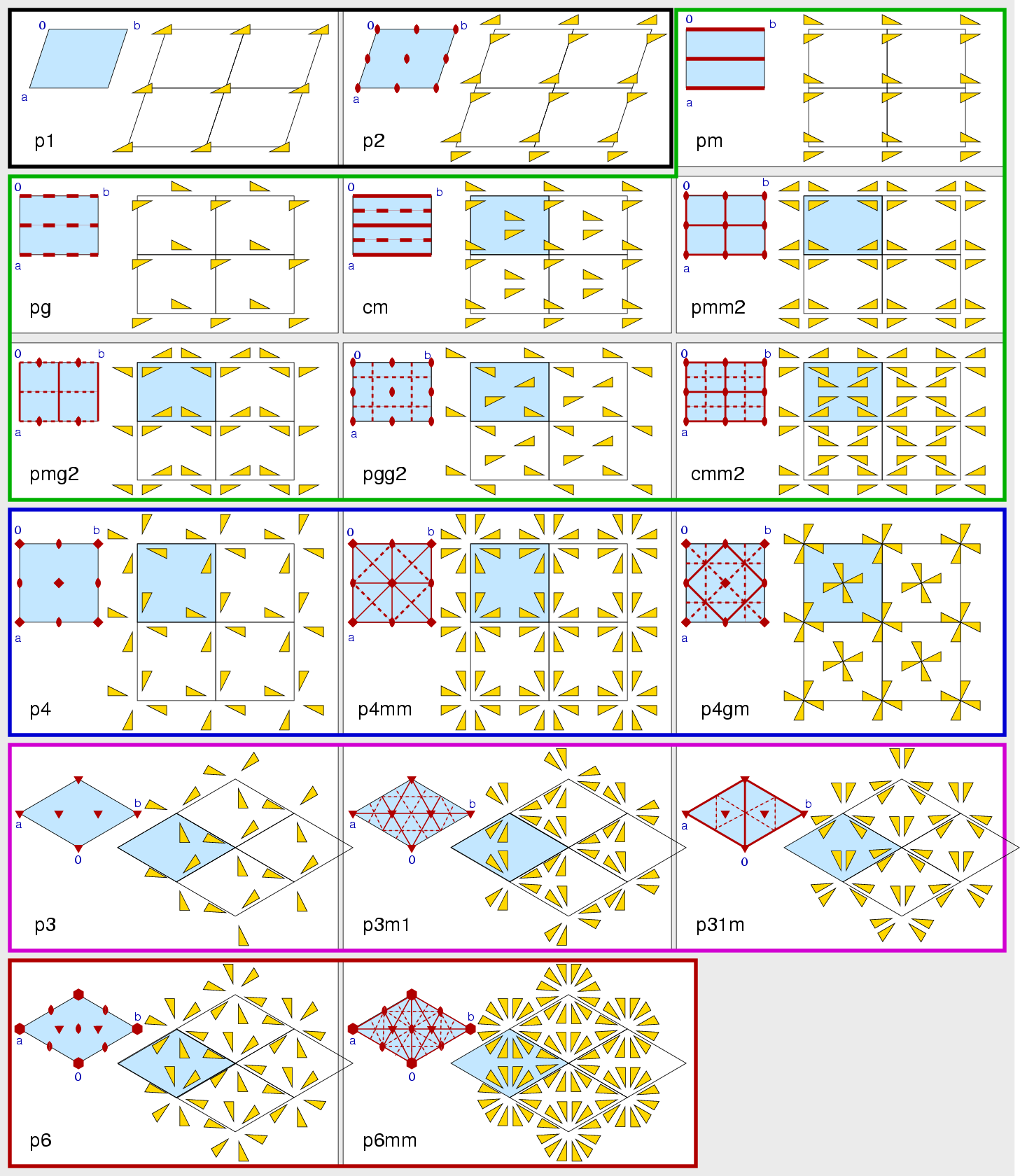
| Abb. II.2.9. Alle 17 Flächengruppen ‣ SVG |
| Hermann-Mauguin-Langsymbol | Flächengruppen | Koordinatensystem |
|---|---|---|
| 1 | p1 | schiefwinklig: a ≠ b, γ beliebig |
| 2 | p2 | |
| 1m1 | pm, pg, cm | rechtwinklig: a ≠ b, γ=90o |
| 2mm | pmm2, pmg2, pgg2, cmm2 | |
| 411 | p4 | quadratisch: a=b, γ=90o |
| 4mm | p4mm, p4gm | |
| 311 | p3 | hexagonal a=b, γ=120o |
| 3m1 | p3m1, p31m | |
| 611 | p6 | |
| 6mm | p6mm |

|
| Abb. II.2.8. Engel und Teufel von M.C. Escher (mit Hilfslinien) |
|
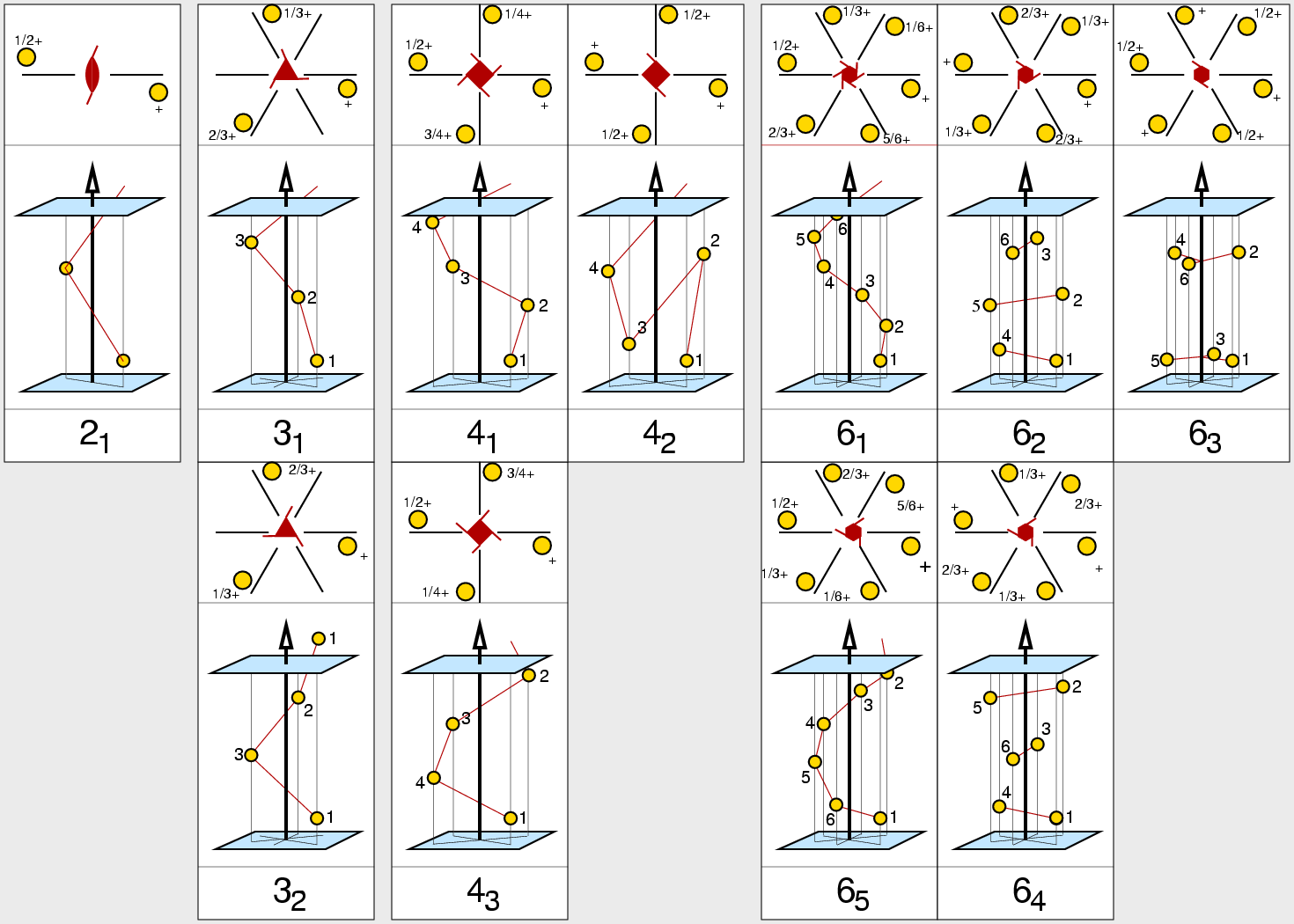
| Abb. II.2.9. Schraubenachsen als neue kombinierte Symmetrieoperationen ‣ SVG |
|
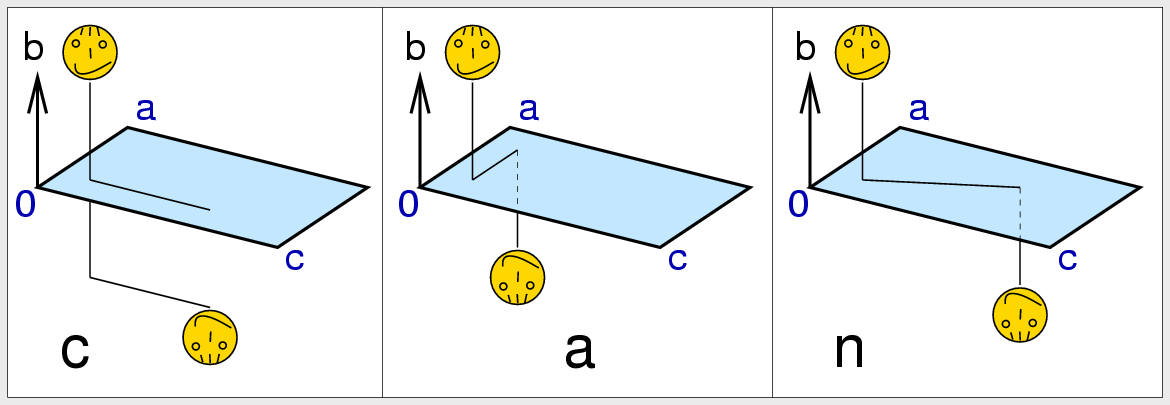
| Abb. II.2.10. Gleitspiegelebenen als neue kombinierte Symmetrieoperationen ‣ SVG |
| Symbol | Bezeichnung | zusätzliche Symmetrieoperationen |
|---|---|---|
| P | primitiv | - |
| I | 2-fach primitiv | x+1/2, y+1/2, z+1/2 |
| C | 2-fach primitiv | x+1/2, y+1/2, z |
| F | 4-fach primitiv | x+1/2, y+1/2, z; x+1/2,y,z+1/2; x, y+1/2, z+1/2 |
| R | 3-fach primitiv | spez. Zentrierung in trigonalen Gittern |

|
| Abb. II.2.11. Zentrierungen in dreidimensionalen Strukturen ‣ SVG |
| Kristall- | Punkt- | Gitter- | Bravaisgittertypen | Blickrichtung | Raumgruppen | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| system | gruppe | konstanten | P | C | I | F | 1. | 2. | 3. | |
| triklin | 1 | a ≠ b ≠ c; α ≠ β ≠ γ ≠ 90o | P | - | - | - | - | - | - | P1 |
| 1̅ | P1̅ | |||||||||
| monoklin | 2 | a ≠ b ≠ c; α = γ = 90o | P | - | C | - | - | [010] | - | P2, P21, C2 |
| m | Pm, Pc, Cm, Cc | |||||||||
| 2/m | P2/m, P21/m, C2/m, P2/c, P21/c, C2/c | |||||||||
| orthorhombisch | 222 | a ≠ b ≠ c; α = β = γ = 90o | P | C | I | F | [100] | [010] | [001] | P222, P2221, P21212, P212121 |
| mm2 | C2221, C222, F222, I222, I212121, Pmm2, Pmc21, Pcc2, Pma21, Pca21, Pnc21, Pmn21, Pba2, Pna21, Pnn2, Cmm2, Cmc21, Ccc2, Amm2, Abma, Ama2, Aba2, Fmm2, Fdd2, Imm2, Iba2, Ima2 | |||||||||
| mmm | Pmmm, Pnnm, Pccm, Pban, Pmma, Pnna, Pmna, Pcca, Pbam, Pccn, Pbcm, Pnnm, Pmmn, Pbcn, Pbca, Pnma, Cmcm, Cmca, Cmmm, Cccm, Cmma, Ccca, Fmmm, Fddd, Immm, Ibam, Ibca, Imma | |||||||||
| tetragonal | 4 | a = b ≠ c; α = β = γ = 90o | P | - | I | - | [100] | [100] [010] | [110] [11̅0] | P4, P41, P42, P43, I4, I41 |
| 4̅ | P4̅, I4̅ | |||||||||
| 4/m | P4/m, P42/m, P4/n, P42/n, I4/m, I41/a | |||||||||
| 422 | P422, P4212, P4122, P41212, P4222, P42212, P4322, P43212, I422, I4122 | |||||||||
| 4mm | P4mm, P4bm, P42cm, P42nm, P4cc, P4nc, P42mc, P42bc, I4mm, I4cm, I41md, I41cd | |||||||||
| 4̅m | P4̅2m, P4̅2c, P4̅21m, P4̅21c, P4̅m2, P4̅c2, P4̅b2, P4̅n2, I4̅m2, I4̅c2, I4̅2m, I4̅2d | |||||||||
| 4/mmm | P4/mmm, P4/mcc, P4/nbm, P4/nnc, P4/mbm, P4/mnc, P4/nmm, P4/ncc, P42/mmc, P42/mcm, P42/nbc, P42/nnm, P42/mbc, P42/mnm, P42/nmc, P42/ncm, I4/mmm, I4/mcm, I41/amd, I41/acd | |||||||||
| trigonal | 3 | a = b ≠ c; α = β = 90o, γ = 120o | (R) | - | - | - | [001] | [100] | [11̅0] | P3, P31, P32, R3 |
| 3̅ | P3̅, R3̅ | |||||||||
| 32 | P312, P321, P3112, P3121, P3212, P3221, R32 | |||||||||
| 3m | P3m1, P31m, P3c1, P31c, R3m, R3c | |||||||||
| 3̅m | P3̅1m, P3̅1c, P3̅m1, P3̅c1, R3̅m, R3̅c | |||||||||
| hexagonal | 6 | a = b ≠ c; α = β = 90o, γ = 120o | P | - | - | - | [001] | [100] [010] [1̅1̅0] | [11̅0] [120] [2̅1̅0] | P6, P61, P65, P63, P62, P64 |
| 6̅ | P6̅ | |||||||||
| 6/m | P6/m, P63/m | |||||||||
| 622 | P622, P6122, P6522, P6222, P6422, P6322 | |||||||||
| 6mm | P6mm, P6cc, P63cm, P63mc | |||||||||
| 6̅m | P6̅m2, P6̅c2, P6̅2m, P6̅2c | |||||||||
| 6/mmm | P6/mmm, P6/mcc, P63/mcm, P63/mmc | |||||||||
| kubisch | 23 | a = b = c; α = β = γ = 90o | P | - | I | F | [100] [010] [001] | [111] [11̅1̅] [1̅11̅] [1̅1̅1] | [110] [110] [011̅] [1̅01] [11̅0] [011] [101] | P23, F23, I23, P213, I213 |
| m3 | Pm3̅, Pn3̅, Fm3̅, Fd3̅, Im3̅, Pa3̅, Ia3̅ | |||||||||
| 432 | P432, P4232, F432, F4132, I432, P4332, P4132, I4132 | |||||||||
| 4̅3m | P4̅3m, F4̅3m, I4̅3m, P4̅3n, F4̅3c, I4̅3d | |||||||||
| m3̅m | Pm3̅m, Pn3̅n, Pm3̅n, Pn3̅m, Fm3̅m, Fm3̅c, Fd3̅m, Fd3̅c, Im3̅m, Ia3̅d | |||||||||
|
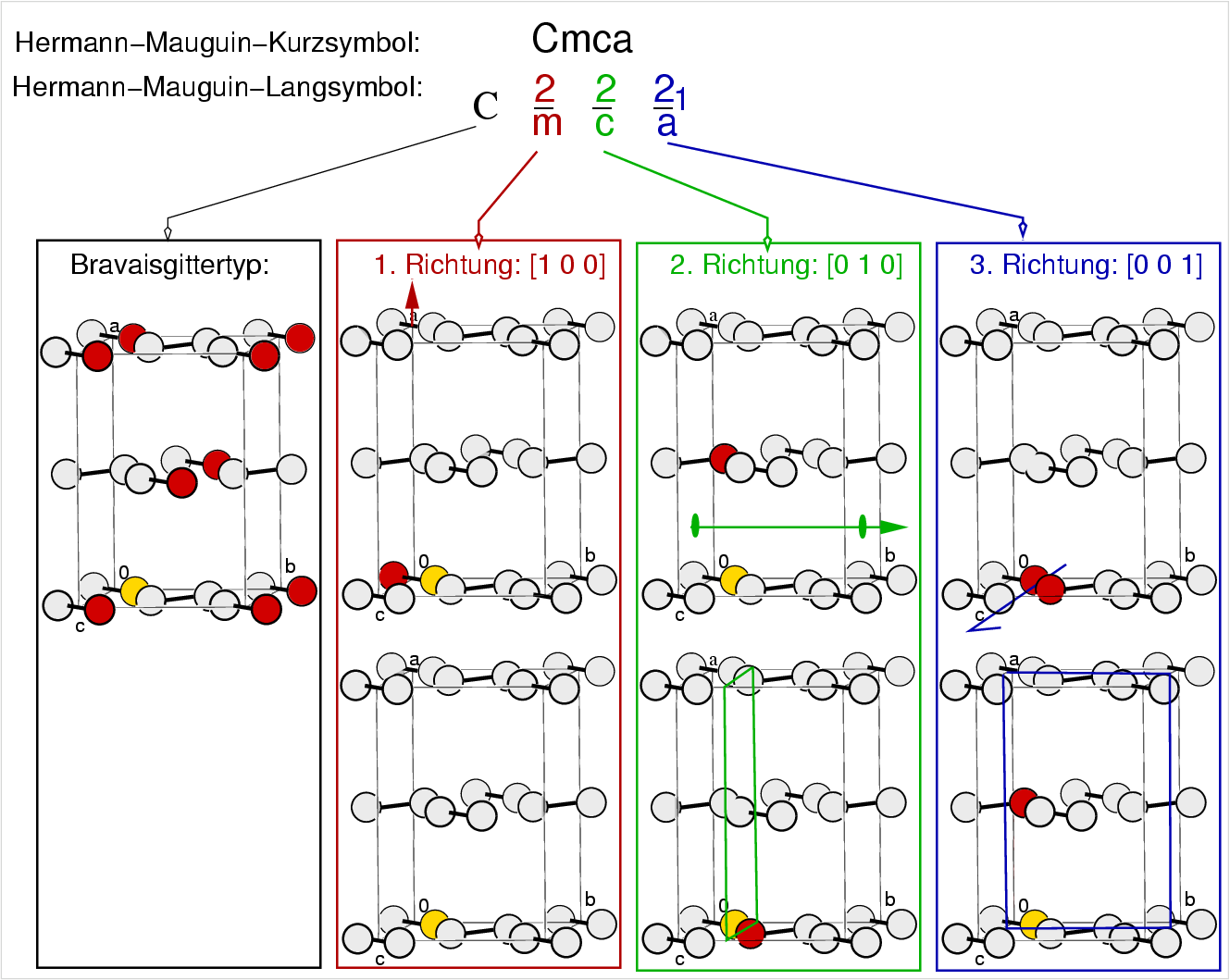
| Abb. II.2.12. Struktur von Iod (mit Veranschaulichung der Symmetrieelemente des Raumgruppensymbols ‣ SVG |
| 1. Richtung | 2. Richtung | 3. Richtung | |
| [100] | [010] | [001] | |
| 2 | 2 | 21 | |
| C | -- | -- | -- |
| m | c | a |
| ← | Inhalt | Einleitung | I. Spektroskopie | II. Beugung | III. Bildgebung | IV. Sonstige Methoden | → |
| cr_home | Metalle | Nichtmetalle | FK-Chemie | Strukturchemie | Interm. Phasen | Oxide | Silicate | Strukturtypen | AFP |