
|
| Abb. II.3.1. Ableitung der Laue-Gleichung ‣ SVG |
| cr_home | Metalle | Nichtmetalle | FK-Chemie | Strukturchemie | Interm. Phasen | Oxide | Silicate | Strukturtypen | AFP |
| ← | Inhalt | Einleitung | I. Spektroskopie | II. Beugung | III. Bildgebung | IV. Sonstige Methoden | → |
Vorlage(n)

|
| Abb. II.3.1. Ableitung der Laue-Gleichung ‣ SVG |
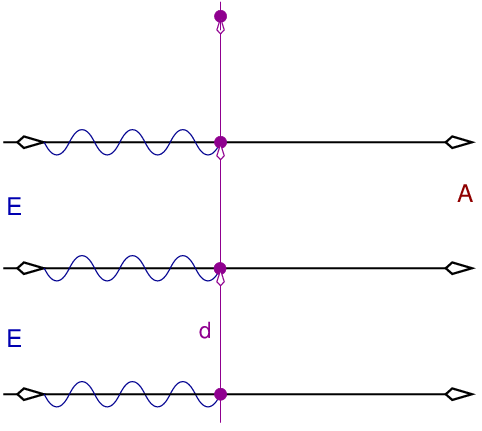
| Abb. II.3.2. Laue-Gleichung zum Durchklicken. (E/A ein/ausfallender Strahl; d: Abstand der Streuzentren; α: Winkel des ausfallenden Strahls gegen den Primärstrahl: Durchklicken zeigt die Interferenz der Kugelwellen für verschiedene Winkel). |
|
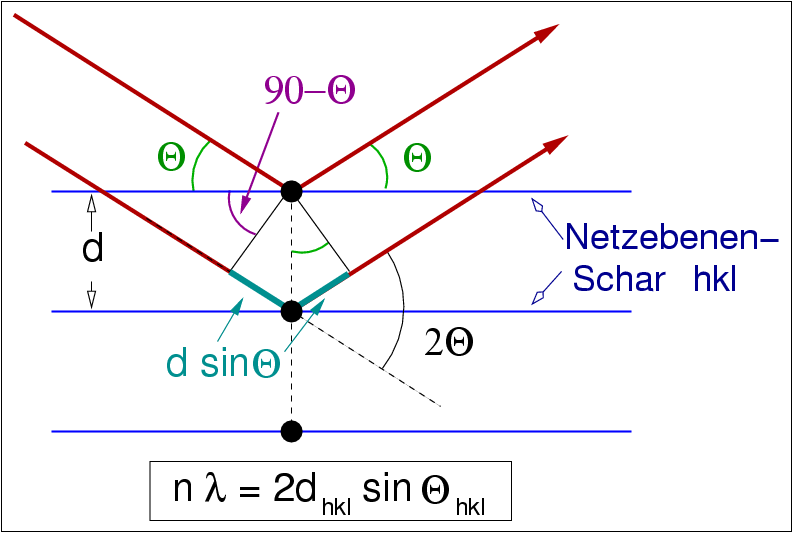
| Abb. II.3.3. Ableitung der Braggschen Gleichung ‣ SVG |

|
| Abb. II.3.4. Atomformfaktoren (Röntgen) und Streulängen (Neutronen) ‣ SVG |
| Symbol | Bezeichnung | zusätzliche Atompositionen | Bedingung für das Auftreten von Reflexen |
|---|---|---|---|
| P | primitiv | - | - |
| C | 2-fach primitiv | x+1/2, y+1/2, z | h+k=2n |
| I | 2-fach primitiv | x+1/2, y+1/2, z+1/2 | h+k+l=2n |
| F | 4-fach primitiv | x+1/2, y+1/2, z | h+k=2n, h+k=2n, k+l=2n |
| x+1/2, y+1/2, z | |||
| x, y+1/2, z+1/2 | |||
| R | 3-fach primitiv | x+1/3, y+2/3, z+2/3 | -h+k+l=2n |
| x+2/3, y+1/3, z+1/3 |
| ← | Inhalt | Einleitung | I. Spektroskopie | II. Beugung | III. Bildgebung | IV. Sonstige Methoden | → |
| cr_home | Metalle | Nichtmetalle | FK-Chemie | Strukturchemie | Interm. Phasen | Oxide | Silicate | Strukturtypen | AFP |