]> Methoden AC, Beugung: Theorie

Vorlesung: Methoden der Anorganischen Chemie

II. Beugungsmethoden

5. Röntgen-Beugung an Einkristallen

Dieser Teil ist vorerst nur vollständig nachlesbar im PDF zum M+K-Kurs 'Kristallographie und Beugung'.

Vorlage(n)

II-5.1: Einkristallstrukturanalyse (PS, PDF)

1. Experimentelles

Basis für eine vollständige Einkristallstrukturanalyse ist die Vermessung der Intensitäten möglichst vieler Reflexe. Hierzu hat man ganz früher Filmmethoden verwendet (Weissenberg-Kamera, Precession-Kamera und Explorer-Kamera). Seit den 70er Jahren des letzten Jahrhunderts sind dagegen Diffraktometer im Einsatz, die zuerst mit einem Szintillationszähler alle Reflexe rechnergesteuert nacheinander vermessen haben. Dazu müssen die Reflexe durch Drehungen des Kristalls in die Detektorebene gebracht werden. Diese Diffraktometer haben daher eine vergleichsweise komplizierte Mechanik, die die Drehung des Kristalls um vier Winkel erlaubt (Vierkreisdiffraktometer). Es gab verschiedene Bauarten mit unterschiedlicher Mechanik (Eulerwiege, Kappa-Geometrie, s. Abb. II.5.1).


Abb. II.5.1. Vierkreisdiffraktometer Enraf-Nonius CAD-4 mit Szintillationszähler und Kappa-Goniometer

Heute werden statt Einzelreflex-Messungen Diffraktometer mit ortsempfindlichen Detektoren verwendet. Dabei gibt es zwei verschiedene Bauarten: Bei den sog. CCD-Detektoren werden Halbleiter-Detektoren verwendet (vgl. Digitalkameras; Abb. II.5.2.). Die Röntgenstrahlung wird in sichtbares Licht umgewandelt und per Lichtleiter auf einem Chip registriert (CCD = Charge Coupled Device). Der Vorteil dieser Detektorbauart ist insbesondere die Geschwindigkeit. Dafür sind die Detektorflächen noch vergleichsweise klein.


Abb. II.5.2. Flächenzähler mit CCD (Fa. Bruker)

Die zweite Bauart sind sog. Image-Plate-Detektoren. Hier werden in großen Platten, die auch gebogen konstruiert werden können, durch die Röntgenstrahlung Seltenerdionen angeregt und können anschließend mit einem Laser ausgelesen und durch intensive Bestrahlung mit sichtbarem Licht wieder gelöscht werden (s. Abb. II.5.3.).


Abb. II.5.3. Flächenzähler mit Image Plate Detektor (Stoe IPDS-II)

Diffraktometer mit Flächenzählern sind von der Mechanik vergleichsweise wenig aufwendig, meistens handelt es sich um Zwei- oder Dreikreis-Systeme. Auf den Images sind die Reflexe (in verzerrter Abbildung des reziproken Gitters) sichtbar. Sie werden zunächst bzgl. ihrer Lage ausgewertet und es wird (nach verschiedensten Algorithmen) ein Gitter gesucht, mit dem alle Reflexe indiziert werden können.

2. Integration, Datenreduktion, Raumgruppenbestimmung

Nach der Indizierung werden die integralen Intensitäten aller Reflexe ermittelt (Integration) und auf Lorentz-, Polarisations- und Absorptionsfehler korrigiert.

I_{hkl} = | F_{hkl} |^{2}_{} L P A

Man erhält so einen großen Satz von Strukturfaktoren F_hkl für viele Reflexe hkl. Aus der Abwesenheit bestimmter Reflexgruppen kann auf Anwesenheit bestimmter translations-behafteter Symmetrieelemente innerhalb der Elementarzelle geschlossen werden (Bestimmung des sog. Beugungssymbols, Hinweis auf mögliche Raumgruppen).

3. Strukturfaktoren - Elektronendichten - Atompositionen

Die mathematische Zusammenhänge zwischen Elektronendichte, F-Werten und Intensitäten sind in Tabelle II.5.1. zusammengestellt.

F_{\vec{h}} = \sum_{j = 1}^{N} f_{j} e^{2 π i (\vec{h} \vec{x_{j}})}

Tab. II.5.1. Reziproker, realer und Patterson-Raum
Raum	reziprok	real	Patterson/Vektor
Ort (Koordinaten)	$\vec{h} = h, k, l$	$\vec{x} = x, y, z$	$\vec{u} = u, v, w$ mit u=x₁-x₂, u=y₁-y₂, u=z₁-z₂
Amplitude	Stukturfaktor F	Elektronendichte ρ	Pattersonfunktion P
Symmetrie	11 Laueklassen	32 Punktgruppen	24 Pattersongruppen
	81 Beugungssymbole aus F²	230 Raumgruppen	Harker-Geraden, -Schnitte
	keine Translationssymmetrie	translationssymmetrisch	translationssymmetrisch

	$F_{\vec{h}} = \int ρ_{\vec{x}} e^{2 π i \vec{h} \vec{x}} d V$	$ρ_{\vec{x}} = \frac{1}{V} \sum_{\vec{h}} F_{\vec{h}} e^{- 2 π i \vec{h} \vec{x}}$	$P_{\vec{u}} = \frac{1}{V} \sum_{\vec{h}} F_{\vec{h}}^{2} e^{- 2 π i \vec{h} \vec{u}}$
			$P_{\vec{u}} = \frac{1}{V} \int_{V} ρ_{\vec{x}} ρ_{\vec{x} + \vec{u}} d V$

Da die Elektronendichte eine periodische Funktion (mit a,b,c als Periodenlängen) ist, können die mathematischen Eigenschaften periodischer Funktionen genutzt werden.
Nach dem Prinzip der Fouriertransformation kann jede periodische Funktion f(x) mit der Periode L als Fourier-Reihe entwickelt werden: $f (x) = \sum_{n} A_{n} e^{2 π i \frac{n x}{L}}$ Dabei sind A_n die Fourier-Koeffizienten: $A_{n} = \frac{1}{L} \int f (x) e^{- 2 π i \frac{n x}{L}} d x$ Der Strukturfaktor läßt sich als Summe über die Atome der Elementarzelle formulieren: $F_{\vec{h}} = \sum_{j = 1}^{N} f_{j} e^{2 π i (\vec{h} \vec{x_{j}})}$ wobei h ein Zeilenvektor (3x1) und x als Spaltenvektor (1x3) darstellt. Er kann aber auch als periodische Funktion der Elektronendichte angegeben werden: $F_{\vec{h}} = \int ρ_{\vec{x}} e^{2 π i \vec{h} \vec{x}} d V$ (d.h. "aquivalent ist die Integration "uber Volumenelemente dV) Vergleich mit Prinzip der Fourier-Synthese (oben) $F_{\vec{h}}$ sind die Fourierkoeffizienten der periodischen Funktion $\rho_x$ $ρ_{\vec{x}} = \frac{1}{V} \sum_{\vec{h}} F_{\vec{h}} e^{- 2 π i \vec{h} \vec{x}}$ Damit wird deutlich, daß die Elektronendichte sich als Fourierreihe der F-Werte entwicklen läßt, bzw. die F-Werte die Fouriertransformierten der Elektronendichte sind. Daraus ergibt sich direkt, daß aus möglichst vielen bekannten F-Werten die Elektronendichtekarte berechnet werden kann. Auf Basis dieser Beziehungen können also Strukturverfeinerung durchgeführt werden.

Die Prinzipien lassen sich an einem eindimensionalen Beispiel gut zeigen. Die eindimensionale Struktur besteht hier aus zwei gleichen Atomen bei 1/3 und 2/3, sie ist als zentrosymmetrisch. Die F-Werte dazu sind in Tabelle II.5.2. angegeben.

Tab. II.5.1. Strukturfaktoren der eindimensionalen Struktur aus Abb. II.5.4.
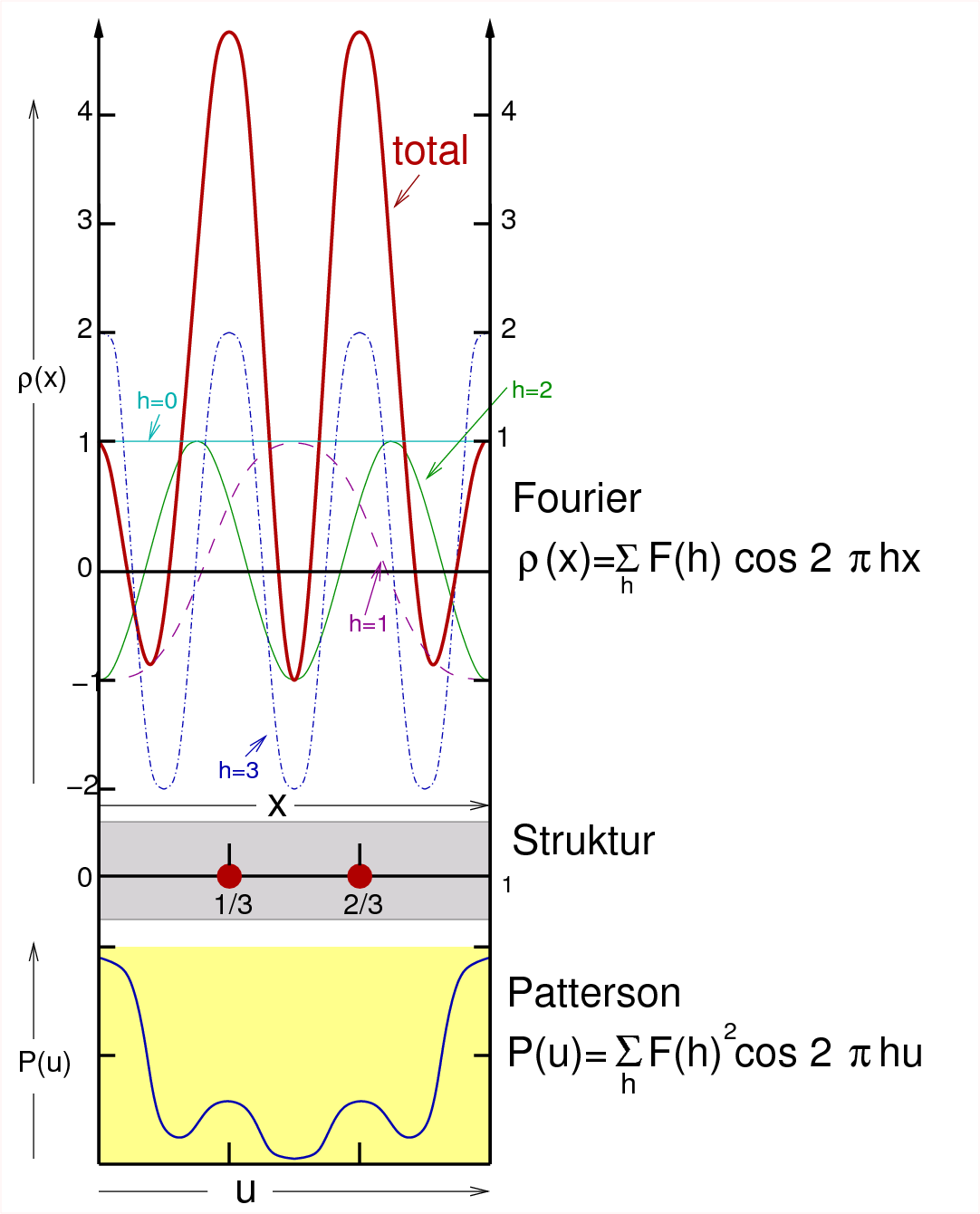
h:	-3	-2	-1	0	1	2	3
F(h)	2	-1	-1	2	-1	-1	2

Die Struktur selber ist in Abbildung II.5.4. Mitte (grau unterlegt) dargestellt.


Abb. II.5.4. Eindimensionale Struktur (Mitte) mit Fourierkarte (oben) und Patterson (unten). ‣ SVG

Berechnet man die einzelnen Beiträge der Summation (s. Abb. II.5.4) $F (h) \cos 2 π h x$ sowie deren Summe (in Abb. II.5.4. in rot) dann wird deutlich, daß die Summe schon bis h=3 eine gute Beschreibung der Elektronendichte ergibt. Je mehr F(h) bekannt sind (möglichst viele Reflexe messen!), desto besser wird die Elektronendichtekarte.

Diese Betrachtungen stellen aber noch keine Lösung des Phasenproblems (Phasenbestimmung!) dar, denn die Strukturfaktoren F sind aus einer Messung nur von der Größe, aber nicht vom Vorzeichen/Phase bekannt.

4. Methoden zur Strukturlösung

Zur Strukturlösung, d.h. Bestimmung der Phasen, gibt es mehrere grundsätzlich verschiedene Verfahren:

Die Pattersonmethode ist die älteste Methode, die auch ohne Rechner durchgeführt werden kann/konnte. Dabei wird die sog. Pattersonfunktion berechnet, indem analog zur Elektronendichte nicht F (die ja unbekannt sind) sondern F² eingesetzt werden: Pu⃗ =1V ∑ h⃗F h⃗ 2e-2 πi h⃗ u⃗ Nach Einsetzen der Formel für die F-Werte folgt: Pu⃗ =1V ∫V ρx⃗ ρx⃗ +u⃗ dV Anschaulich erhält man also Maxima in der Patterson-Funktion an den Orten u, an denen die Kombinationsvektoren zweier Atome liegen (Vektorraum). Erkennbar werden also Abst"ande, vom jeweiligen Atom aus gesehen. Die Nachteile der Pattersonfunktion sind:
- Es gibt ein sehr breites Maximum bei 0,0,0.
- Die Peakhöhen hängen immer von zwei (!) Elektronendichten ab.
- Die Peaks sind viel breiter als bei der Elektronendichte (Fourierkarte der F-Werte).
- Die P-Funktion hat sehr viele Peaks, da bei jedem Interkombinationsvektor ein Maximum entsteht.
Daher sind Pattersonmethoden nur für Schweratomstrukturen (z.B. Metallkomplexe) geeignet, da sonst die Information über die Atompositionen extrem stark 'verschmiert' ist. Für das o.g. eindimensionale Beispiel ist die Pattersonfunktion in Abb. II.5.4 eingezeichnet. Man erkennt ein hohes Maximum bei 0 und deutlich breite Peaks als in der Fourierkarte der F-Werte. Wenn nicht ein Atom sehr viel 'schwer' ist als die übrigen, entstehen keine definierten Maxima mehr.
Die Direkten Methoden nutzen die Leistung von Rechnern zur Phasenbestimmunge aus (Brute force). Sie sind heute die für Strukturen mit gleichen Streuen am meisten verwendeten Methoden. Die direkten Methoden basieren auf statistischen Aussagen, die wiederum auf zwei Grundprinzipien aufbauen:
- Die Elektronendichte kann nicht negativ werden.
- Die Elektronendichte ist an den Atompositionen konzentriert.
Verwendet werden verschiedene Aussagen (hier ohne Beweis!) zur Reflexstatistik:
- Harker-Kasper-Ungleichungen (1948)
- Sayre-Gleichung (1952) $s (\vec{h_{1}}) s (\vec{h_{2}}) s (\vec{h_{1}} + \vec{h_{2}}) \approx 1$ Hierbei bedeutet s 'das Vorzeichen von' und ≈ 'ist mit einer bestimmten Wahrscheinlichkeit', wobei diese Wahrscheinlichkeit mit der Größe des F-Wertes steigt. Die Sayre-Gleichung stellt also eine Beziehung zwischen den Vorzeichen dreier Reflexe her (Triplett-Relation).
- Die Erweiterung auf Quartett-Beziehung usw. erlaubt auch Aussagen bei nichtzentrosymmetrischen Strukturen.
Praktisch werden Rechnerprogramme (sehr bekannt: Shelxl, von G. Sheldrick, Göttingen) verwendet, die zunächst starke Reflexe wählen. Dann werden die Phasen beliebig zugeordnet und diese Zuordnung mittels der Sayre-Gleichung auf Konsistenz geprüft. Wenn die Gleichungen weitgehend korrekt sind, wird durch eine anschließende Fourier-Synthese das Strukturmodell berechnet.
Charge-Flipping
Dual-Space-Methoden

5. Strukturverfeinerung

Theorie s.o., praktisch Wenn etwas mehr als ca. die Hälfte der Elektronen korrekt lokalisiert ist, sind die meisten Phasen bereits richtig bestimmt und mittels Fourier-Synthesen (s.o.) können gute Elektronendichtekarten berechnet werden. Für die Ermittlung weiterer Atompostionen werden Differenz-Fouriersynthesen durchgeführt, die dann zu Differenzelektronendichten führen. Bei den weiteren Strukturverfeinerung (Least-Squares-Verfahren) ist zu beachten, daß gute Verfeinerungen ca. 10 bis 20 Reflexe pro freiem Parameter erfordern. Dabei ist zu berücksichtigen, daß i.A. pro Atom insgesamt neun Parameter, außer den drei Lageparametern x, y, z noch die anisotropen Verschiebungsparameter, die die harmonische Bewegung der Atome beschreiben, verfeinert werden. Durch die Atombewegung fallen die Strukturfaktoren F mit Θ stärker ab. (s. Abb. II.5.5.)


Abb. II.5.5. Temperaturfaktoren B ‣ SVG

In der harmonischen Beschreibung gilt:

F_{\vec{h}} = \sum_{j = 1}^{N} f_{j} e^{2 π i (\vec{h} \vec{x_{j}})} e^{- B_{j} \frac{s i n^{2} Θ}{λ^{2}}}

Meist werden statt einem isotropen Wert B auch noch harmonische, anisotrope Bewegung zugelassen (symmetrischer 3x3-U-Tensor). Diese anisotropen Verschiebungsparameter U_ij beschreiben die Hauptachsen und die Orientierung des Bewegungsellipsoids.

6. Ergebnisse einer Einkristallstrukturanalyse

Zur vollständigen Dokumentation einer Strukturanalyse werden meist nicht nur die Atompositionen, sondern auch die 'Schwingungsellipsoide' (mit bestimmten Aufenthaltswahrscheinlichkeiten, sogenannte ORTEP-Darstellung) dargestellt. Für I₂ ist dies in Abbildung XXX zu sehen: i2.ort.ps Aus den Atomlagen können dann leicht berechnet werden:

Atomabstände (auf ca. 0.1-0.5 pm genau)
Winkel (auf ca. 0.3-1.0^o genau)
beste Ebenen, ...
thermische Bewegung (Librationen; Translationen)

Die Ergebnisse wandern in Strukturdatenbanken, von denen es verschiedene gibt:

Leider ist davon nur die Protein-Database frei zugänglich.

7. Probleme und Grenzen der Methode

Zwillinge, die zusätzliche Symmetrie im Beugungsbild bewirken.
Fehlordnung, die zu diffusen Streubeiträgen führt.
Bestimmung von H-Atompositionen (s. Neutronenbeugung)
Unterscheidung von Atomen mit gleichen Elektronenzahlen (s. Neutronenbeugung)

Literatur

Außer vielen speziellen Büchern

CHIUZ-Artikel: Egbert Keller (Kristallographie FR) 3, S. 71, 1982
W. Massa: Kristallstrukturbestimmung (für Anwender bei Diplom/Dr.-Arbeiten sehr geeignet)
C. Giacovazzo et al.: Fundamentals of Crystallography, Oxford Science Publications.
Discus (Proffen, Neder)

IV. Sonstige Methoden

Oxide

AFP