]> Methoden AC, NMR

Vorlesung: Methoden der Anorganischen Chemie

I. Spektroskopische Methoden

3. NMR-Spektroskopie

Vorlage(n)

Vorlage I-3.1: Prinzipien der NMR, Beispiel-Spektren I (PS, PDF)
Vorlage I-3.2: Beispiel-Spektren II (PS, PDF)

Aus der Organischen Chemie ist die NMR-Spektroskopie als Methode sehr gut bekannt, besonders die Auswertung von Spektren für Protonen ¹H ist allgemein gut bekannt. Daher soll hier lediglich das Prinzip der Methode mit etwas Theorie rekapituliert werden. Die komplizierte Theorie und spezielle Pulsfolgen werden in der physikalischen Chemie (PC-F-Praktikums-Versuch) behandelt. Hier soll also nur das Prinzip der Methode kurz wiederholt werden und dabei auf Kerne mit einem Kernspin von I>1/2 erweitert werden. Dann werden einige typische Spektren anorganischer Systeme vorgestellt, zweidimensionale Spektren werden am Beispiele der Borane diskutiert. Eine weitere Ergänzung betrifft die Untersuchung fester Proben (MAS-NMR).

Die weitere Gliederung ist danach

Prinzip der Methode, Apparate, Spektren
Beispiele aus der anorganischen Chemie (mit Spektren und daraus ableitbaren Informationen
Festkörper-Kernresonanz-Methode (MAS-NMR)
Untersuchungen dynamischer Prozesse

1. Prinzip der Methode, Apparate, Spektren

Die NMR-Spektroskopie ist die wichtigste Methode zur Bestimmung der lokalen Struktur um ausgewählte Kerne in Molekülverbindungen. Sie ist nach dem in der Einleitung gesagten eine Methode, die in praktischen allen chemischen Instituten zum Einsatz kommt. Das Prinzip ist die Orientierungsumkehr von im Magnetfeld ausgerichteten Kernspins. Die relevanten Energien liegen bei Spinenergien, d.h. extrem niedrigen Energien:

Die Wellenlängen λ liegen im UKW-Bereich, d.h. zwischen 1 m und 1 cm.
Die zugehörigen Frequenzen ν betragen 150 kHz bis 15000 MHz, d.h. 15 GHz.
In Energien ausgedrückt liegt die NMR-Spektroskopie bei nur 0.1 J/mol oder 10^-6 eV.

Darauf folgt, dass Quelle bzw. Detektor Radio-Sender- bzw. Empfänger-Spulen sind (Entstörungsproblem!) Die ESR-Spektroskopie beruht analog auf der Umkehr von Elektronenspins. Sie liegt bei etwas höheren Energien, was auf den Massenunterschied zwischen Elektronen und Kerne zurückzuführen ist (s.u.).

Zum Verständnis des Prinzips der Methode wird zuerst anhand eines Einzelkerns betrachtet:

Welche Kerne haben einen Kernspin, also Spinquantenzahl I ≠ 0?
Welcher mechanische Eigendrehimpuls/Spin folgt draus?
Welches magnetische Dipolmoment liegt vor? (Stärke des Elementar-Magneten)
Welche Ausrichtungen mit welchen potentiellen Energien erfahren die rotierenden (mechanisch!) magnetischen (!) Dipole im homogenen äußeren Magnetfeld B_z ?
Welche Eigenenergien kann das Spinsystems quantenmechanisch annehmen (vgl. PC III-IV)?

Aus dem Vergleich der Energien von 4. und 5. folgen dann die möglichen Experimente und Apparate für die NMR-Spektroskopie.

Kerne mit Spin I ≠ 0, d.h. mit einem Kernspin zeigen quantenmechanisch große Ähnlichkeiten und Effekte wie die gut bekannten Elektronen.

Elektronen sind (vgl. UV/VIS-Spektroskopie) Fermion mit einer Spinquantenzahl von s=1/2. Der Betrag des Spins bzw. des mechanischen Eigendrehimpulses zeigt eine Betragsquantelung:

| \vec{s} | = \sqrt{s (s + 1)} ħ

Die Orientierungsquantenzahl (m_s), die die Orientierung im Magnetfeld beschreibt, kann nur die Werte m_s = -s, ... +s, d.h. ± 1/2 annehmen. Daraus ergeben sich 2s+1=2 Einstellungen im Feld, die ohne angelegtes Feld entartet sind. Die z-Komponenten des Elektronenspins (Richtungsquantelung) kann nur Werte von

s_{z} = m_{s} ħ = \pm \frac{1}{2} ħ

(Richtungsquantelung) annehmen. Das rotierende geladene Teilchen ist ein magnetischer Dipol (Minimagnet) mit einem Dipolmoment

| \vec{μ} | = - γ β_{B} \sqrt{s (s + 1)}

in [J/T] wobei β_B das Bohrsche-Magneton und γ das gyromagnetische Verhältnis bedeutet.

Isolierte Nukleonen (Protonen p und Neutronen n) alleine sind ebenfalls Fermion mit einem Einzeldrehimpuls von s=1/2. Die Gesamtkerne zeigen einen Kernspin (mit Spinquantenzahl I), der durch Vektoraddition von p- und n-Spin (wie genau ist nur durch die aktuelle Kernphysik erklärbar) zustande kommt. Hierfür gelten jedoch folgende einfache Regeln:

Tab. I.3.1. Kernspinquantenzahlen aus Massen- und Kernladungszahlen
Kernspin-Quantenzahl	halbzahlig	0	ganzzahlig
Massenzahl	u	g	g
Kernladungszahl	g oder u	g	u

Danach sind nur g-g-Kerne NMR-still. Diese sind jedoch - wegen der Entstehung der Elemente aus ⁴₂He - relativ häufig. Außer ¹H ist für die Organische Chemie vor allem ¹³C ein wichtiger Kern. In Tabelle I.3.2. sind weitere für anorganische Verbindungen wichtige NMR-Kerne mit Kernspinquantenzahl I, gyromagnetischem Verhältnis γ und relativer Frequenz/Empfindlichkeit bzgl. ¹H zusammengestellt.

Tab. I.3.2. NMR-Kerne mit Spin, Häufigkeit und Empfindlichkeit
Isotop	Kernspin	Häufigkeit [%]	γ [10⁷ rad T^-1s^-1]	rel. Frequenz [MHz]	rel. Empfindlichkeit
¹H	1/2	99.985	26.7519	100	1.0
²H	1	0.015	4.1066	14.7	1.5 ^. 10^-6
¹⁰B	3	19.6	2.8746	10.7	3.9 ^. 10^-3
¹¹B	3/2	80.4	8.5843	32.1	1.3 ^. 10^-1
¹³C	1/2	1.11	6.7283	76.2	5.8 ^. 10^-7
¹⁴N	1	99.6	1.9338	7.2	1.0 ^. 10^-3
¹⁵N	1/2	0.37	-2.712	10.1	3.9 ^. 10^-6
¹⁹F	1/2	100.0	25.181	94.1	8.3 ^. 10^-1
²⁷Al	5/2	100.0	6.9760	26.1	2.1 ^. 10^-1
³¹P	1/2	100.0	10.841	40.5	6.6 ^. 10^-2
⁷³Ge	9/2	7.8	-0.9357	3.5	1.1 ^. 10^-4
¹⁹⁷Au	3/2	100	4.2342	16.2	51.4 ^. 10^-1

Diese Kerne haben also einen mechanischen Eigendrehimpuls/Spin, dessen Betrag und Einstellungen im Feld ähnlich wie oben und im Abschnitt über UV/VIS-Spektren für das Elektron beschrieben, quantisiert sind. Für Kerne mit der Spin/Eigendrehimpus-Quantenzahl I kann der Betrag des Spins/Eigendrehimpulses nur die Werte |I⃗ |=I (I+1) ħ annehmen, die Länge des Drehimpulsvektors ist für jeden Kern also fix. Die Orientierungs-Quantenzahl (M_I) beschreibt die quantenmechanisch erlaubten Orientierungen im Magnetfeld. Sie kann die Werte M_I = -I, ... +I annehmen und beschreibt die erlaubten z-Komponenten des Kern-Spins im äußeren Magnetfeld (I_z = M_I ħ, Richtungsquantelung). Generell gibt es wieder jeweils 2I+1 Einstellungen im Feld (Multiplizität; ohne Feld entartet), d.h. bei
- ¹H mit I=1/2: 2 Einstellungen
- ¹⁴N mit I=1: 3 Einstellungen (s. Abb. I.3.1.)
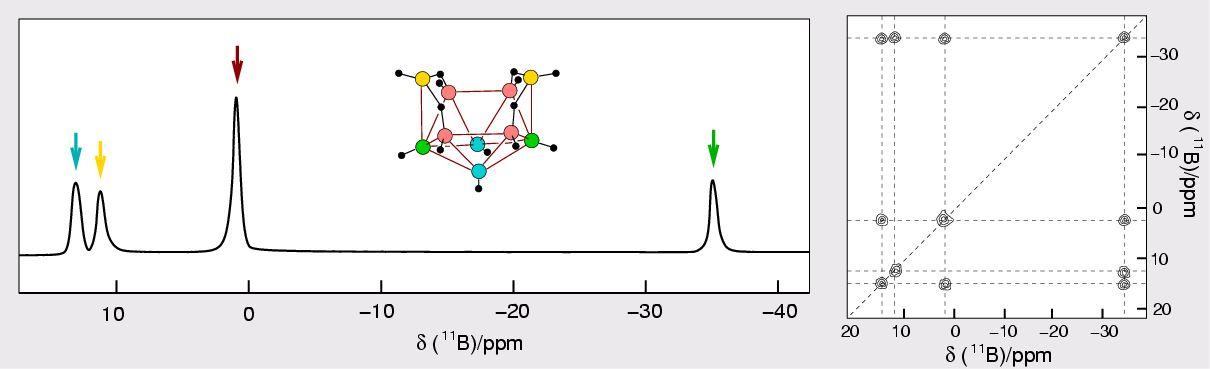
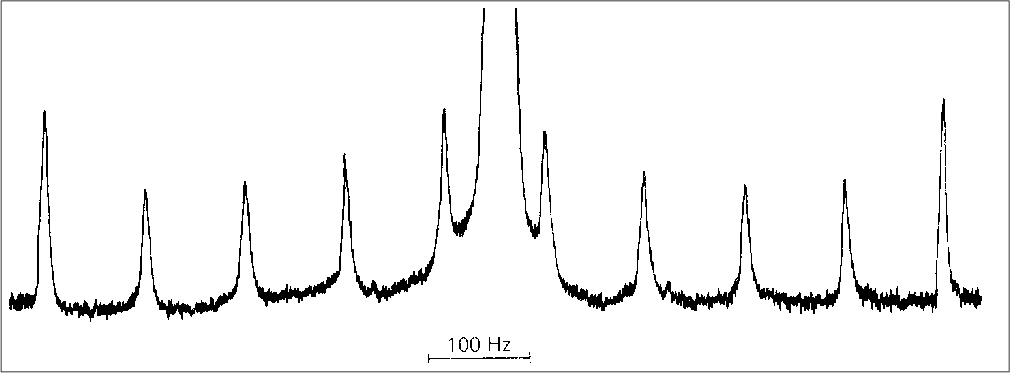
- ¹¹B mit I=3/2: 4 Einstellungen und bei
- ⁷³Ge mit I=9/2 sogar 10 Einstellungen
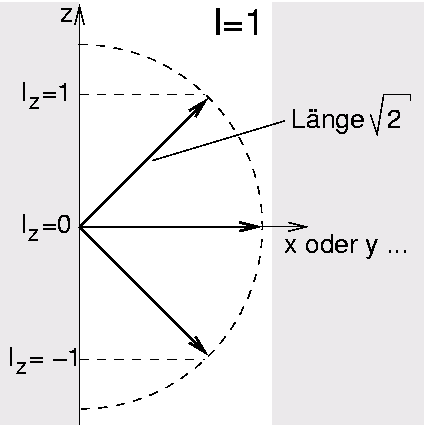
und damit zeigt z.B. das ¹H-Spektrum von German, GeH₄, wegen der (2I+1)-fachen Aufspaltung auch 10 Linien (s. Abb. I.3.X.)

Abb. I.3.1. Drehimpuls und I_z für Kerne mit I=1 ‣ SVG

Im halbklassischen Bild liegt die Richtung I_z durch das äußere Feld fest, die beiden anderen Komponenten sind unbestimmt. Die Komponenten von I⃗ in x- und y-Richtung sind im zeitlichen Mittel = 0, d.h. man kann sich die Spins als um die z-Achse umlaufend vorstellen.
Das magnetisches Dipolmoment μ, das der Kern als rotierendes geladenes Teilchen aufweist (Kreisströme1), ist proportional zum Drehimpuls: $\vec{μ} = γ \vec{I}$ Damit gilt auch für die z-Komponenten im magnetischen Feld: $μ_{z} = γ I_{z} (Gl. 1)$ Das Dipolmoment ist also zum Drehimpuls proportional, die Propotionalitätskonstante γ nennt man gyromagnetisches Verhältnis, da es dem Quotienten aus magnetischem Moment und mechanischem Drehimpuls entspricht. γ ist für die verschiedenen Kerne nicht berechenbar, die Werte für die Konstanten der einzelnen Kerne sind in Tabelle I.3.1. angegeben. Die Werte von γ liegen zwischen -3 und 27 10⁷ rad T^-1 s^-1. Meist sind sie positiv, in seltenen Fällen aber auch negativ. Für das Dipolmoment μ (die Stärke des Magneten) ergeben sich damit Werte zwischen -2.1 μ_N und 5.5 μ_N, wobei das Kernmagneton μ_N (entsprechend dem Bohrsches Magneton μ_B = 1836 μ_N für Elektronen) eine fundamentale Nukleonenkonstante ist: $μ_{N} = \frac{e h}{4 π m_{N} c}$ Dipolmomente und μ_N haben die Einheit Am² (Strom*Fläche) = (kg s^-2 T^-1) m² = J/T (Energie/Magnetfeld).
Die Wechselwirkung des magnetischen Dipols μ mit einem äußerem Feld B_z kann makroskopisch mit einer rein mechanische Betrachtung (makroskopische Minimagnete im grossen homogenen Magnetfeld) beschrieben werden. Die Minimagnete richten sich im homogenen äußeren Feld in N-S-Richtung aus. Ist keine mechanische Rotation (also kein Drehimpuls) vorhanden, dann schwingen sie um die Feldachse, ohne Reibung unendlich lange. Bei mechanischer Rotation um die eigene N-S-Achse der Minimagnete (d.h. wenn ein Drehimpuls vorliegt) beobachtet man den gyroskopischen Effekt (vgl. mechanisches Gyroskop HIER): Es kommt zur Präzession der Magneten um die Feldachse. Die Präzessions-Frequenz ν₀ hängt dabei ab vom äußeren Feld B_z (ν ist groß, wenn B_z groß ist) und vom Verhältnis des magnetischen Momentes und des mechanischen Drehimpulses, d.h. von γ (je größer γ ist, umso größer ist die Präzessionsfrequenz). Die Frequenz ν₀ ist also groß, wenn die Magnetnadel stark (ν groß) und der mechanische Drehimpuls klein ist. Genau gilt (auch makroskopisch!): $ν_{0} = γ \frac{B_{z}}{2 π} (Gl. 2)$ Die Präzessionsfrequenz ν₀ heißt Lamor-Frequenz.

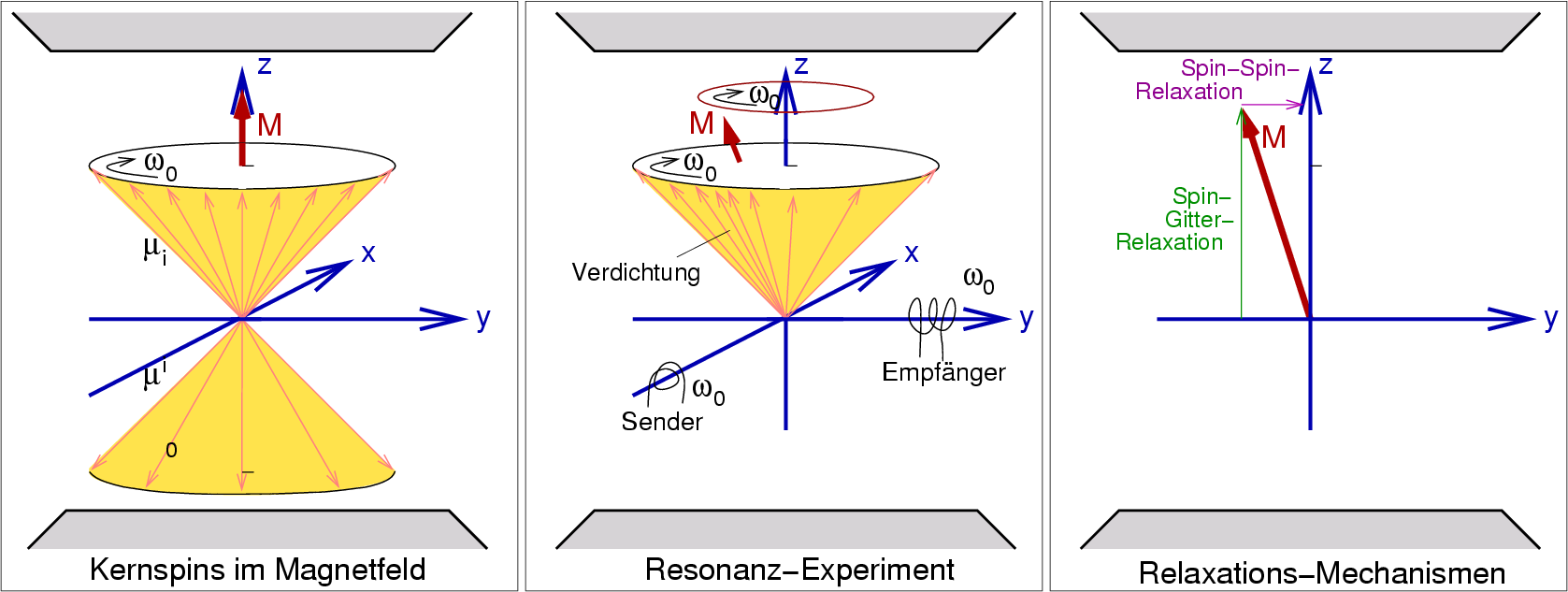
Abb. I.3.2. Funktions-Prinzip der NMR-Spektroskopie ‣ SVG

Für die potentielle Energie E_pot dieses Zustandes, die sogenannte Zeeman-Energie, folgt wegen E= h ν aus Gl. 2 (durch Multiplikation mit h) $E = h ν_{0} = ħ γ B_{z} (Gl. 3)$ Diese Energie kann nun mit den Eigen-Energien des quantenmechanischen Spin-Systems verglichen werden und daraus ergibt sich die Resonanz-Bedingung der NMR-Spektroskopie:
Für die Eigenenergien des Spinsystems (quantenmechanisch, PC II/III) ergeben sich folgende Energie-Eigenwerte (ohne Beweis): E=-γM l︸ ħBz (Gl. 4) Für die Spinumkehr (z.B. von +1/2 nach -1/2) gilt als Auswahlregel: ΔMl =±1 Damit folgt für alle Kerne, daß nur Übergänge erlaubt sind für die gilt: ΔE =γ ħBz (Gl. 5) Der Vergleich dieser quantenmechanischen Eigenenergiedifferenzen ΔE (Gl. 5) mit den potentiellen Energien des mechanischen Systems (Gl. 3, Zeemann-Energie) zeigt, daß die Lamor-Frequenz (in Hz, Mechanik!) der Energiedifferenz ΔE zwischen den quantenmechanischen Energie-Niveaus entspricht. Daraus folgt, daß durch die Einstrahlung von ν₀ genau die Energie ΔE = h ν₀ zugeführt werden kann, die zum Spinflip erforderlich ist. Aus Gleichung 5 folgt unmittelbar, daß sich ΔE linear mit B_z ändert (s. Abb. I.3.3.).

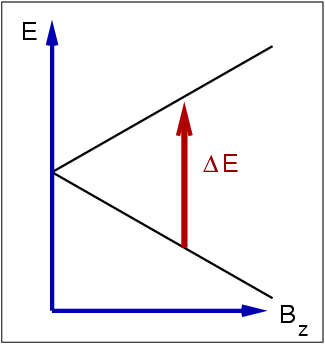
Abb. I.3.3. Abhängigkeit von ΔE vom Magnetfeld B_z ‣ SVG

Daraus folgt für den apparativen Aufbau, daß möglichst starke Magnete erforderlich sind, um möglichst große Energiedifferenzen zu bewirken. Normale Permanentmagnete haben Feldstärken von 1-2 T, normale Elektromagnete zwischen 1.8-2.3 T und supraleitende Magnete (He-Kühlung, z.B. Nb₃Sn) bis 13 T (AC alt: 200 MHz = 4.67 T; AC neu: 400 MHz WB). Die Energie-Aufspaltung ist für jeden Kern (d.h. bei gleichem γ) nur von B_z abhängig, z.B.
- ¹H bei 2.3 T: 100 MHz
- ¹³C bei 2.3 T: 25 MHz
Die Gesamtmagnetisierung M des Systems ist von der Besetzung der Energie-Niveaus abhängig. Diese folgt der Boltzmann-Verteilung. Da aber ΔE sehr klein gegen kT ist (Hochtemperatur-Näherung für die Boltzmann-Verteilung), liegt fast eine Gleichverteilung der Spins vor. $\frac{N_{+}}{N_{-}} \propto 1 + \frac{2 μ B}{kT}$ Beispielsweise sind bei 100 MHz und B=2.34 T im unteren Niveau 1 000 016, im oben 1 000 000. Aus dieser leicht unterschiedlichen Besetzung ergibt sich eine resultierende Gesamtmagnetisierung M (s. roter Pfeil in Abb. I.3.2.)
Mit dieser Gesamtmagnetisierung sind nun verschiedene Experimente möglich:
- Früher hat man im Frequenzabtastverfahren (sog. CW = Continuous Wave) ν mit der Senderspule durchgefahren. Wenn die Frequenz der eingestrahlten Strahlung der Lamorfrequenz entspricht, kommt es zum Umklappen der Spins (Spinflip), die Strahlung wird absorbiert. Der Vektor M verbleibt in z-Richtung, ändert jedoch sein Länge. In der Empfänger-Spule, die um die Probe herum angeordnet ist und senkrecht zur Senderspule liegt, wird ein Induktionsstrom induziert. Diese Methode ist sehr langsam, da die Frequenzen langsam durchgefahren werden müssen.
- Heute wird als Standard-Verfahren 1D-Fourier-Transform-NMR (FT-NMR) verwendet. Ein kurzer (wenige Mikrosekunden), nur wenige Grad des Lamor-Umlaufs langer 90^o-Frequenzpuls, der alle Frequenzen zugleich enthält und ein kleines Magnetfeld in dieser Richtung aufweist, bewirkt die Ausrichtung der energetisch passenden Gesamtmagnetisierung M in die x-y-Ebene. Die Spins werden auf dem Kegelmantel verdichtet (Abb. I.3.2. Mitte, hier sind nur noch die Nichtgleichgewichts-Spins dargestellt!), die Gesamtmagnetisierung gegen die z-Richtung des Magneten ausgelenkt (Quermagnetisierung). Nach dieser Einstrahlung kehrt die Gesamtmagnetisierung (aufgrund verschiedener Relaxationsprozesse, s.u.) mit der Lamor-Frequenz in den Gleichgewichtszustand zurück, in der Empfängerspule (in y-Richtung) wird das mit der Zeit exponentiell abfallende Signal registriert (sog. FID = free induction decay). Die Pulse werden ca. alle 3-5 s wiederholt, und die Spektren akkumuliert. Die Fourier-Transformation des Gesamt-FIDs (Zeitspektrum) ergibt dann das bekannte Frequenz-Spektrum (s. Abb.I.3.4).
  
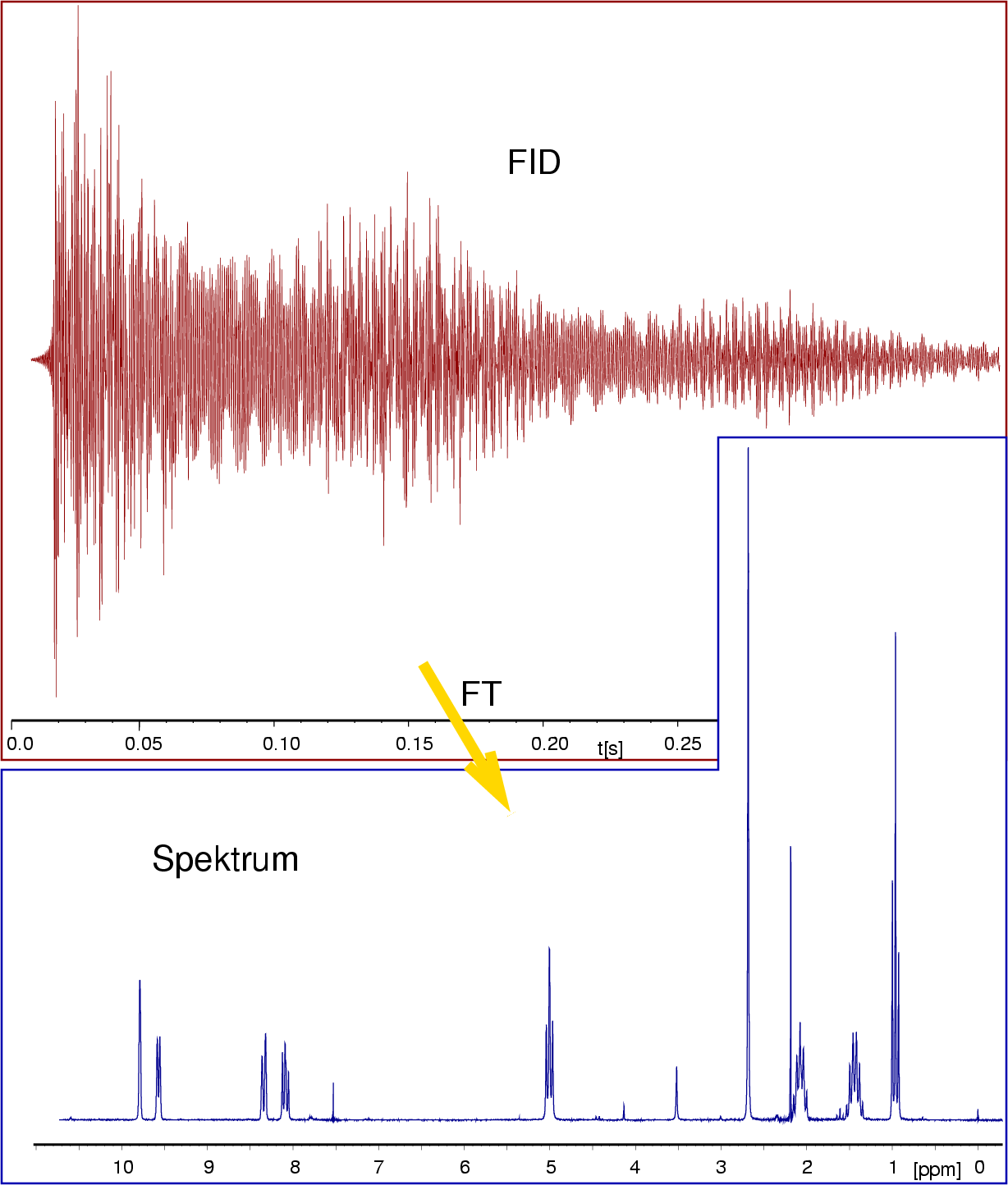
  Abb. I.3.4. FID (rot) und das durch Fourier-Transformation erhaltene Spektrum (blau) ‣ SVG
  
  Mit Hilfe dieser Technik ist leicht eine Breitbandentkopplung möglich, bei gleichzeitiger konstanter Einstrahlung der Frequenzen der koppelnden Kerne erhält man entkoppelte Spektren.
- Bei modernen Mehrdimensionalen-NMR-Techniken werden meist komplizierte Pulsfolgen (Spin-Echo-Experiment) gefahren (2D heteronukleare NMR (COSY=COrrelated SpectroscopY). Einige auf diese Weise erhaltene Spektren werden unten bei den Beispielen gezeigt, die Details dieser Messungverfahren überlassen wir der PC.
Relaxationsmechanismen
Nach der Störung des Gleichgewichts kehren die Spins durch verschiedene Relaxations-Prozesse in das Boltzmann-Gleichgewicht zurück. Je nach Messverfahren können die einzelnen Relaxationsprozesse auch einzeln vermessen werden. Man unterscheidet in (s. Abb. I.3.2. rechts):
1. Bei der Spin-Gitter- oder longitudinalen Relaxation oder T₁ erfolgt ein Austausch mit der Umgebung (dem Gitter), in dem immer passende Frequenzen vorhanden sind. Der energetisch höhere Zustand wird wieder in den tieferliegenden umgewandelt. Die typischen Zeiten für diese Prozesse, die verglichen mit der Lamor-Frequenz extrem groß sind, liegen bei Festkörpern bei 10^-2 bis 10⁴ s, d.h. die Gesamtmagnetisierung wird nur sehr langsam wieder aufgebaut. Die Zeiten liegen bei flüssigen Proben zwischen 10^-4 und 1 s, meist bei ca. 10^-2 s.
2. Bei der Spin-Spin- oder transversale Relaxation oder T₂ kommt es zur Wechselwirkung der 'Ungleichgewichts'-Spins untereinander, dadurch wird die Verdichtung abgebaut. Typische Zeiten sind im Festkörper 10^-4 s (sehr schnell!), in flüssigen Proben typischerweise ca. 10^-2 s.
Linienbreiten: Aufgrund der Unschärferelation $δ E τ \approx ħ$ ist die Relaxationszeit τ der Linienbreite umgekehrt proportional. Sehr kleine Relaxationszeiten bewirken eine große Energie-Unschärfe, d.h. Linienbreite und umgekehrt. Für τ = 1s ergeben sich sehr schmale Signale von 0.1 Hz, ist τ dagegen nur 10^-4 s, dann sind die Signale mit 1000 Hz extrem breit. Dies ist z.B. bei Festkörpern der Fall, wo T₂ i.A. sehr klein ist (besser: Auflösen oder MAS).

Magnetische Wechselwirkungen: Informationen aus NMR-Spektren

Für die Anwendung der NMR-Spektroskopie als Standard-Methode in der Chemie sind drei Arten magnetischer Wechselwirkung wichtig:

Chemische Verschiebung: Das von außen angelegte Magnetfeld weist an den verschiedenen Kernen nicht unbedingt den gleichen Wert auf, die unterschiedliche elektronische Umgebung der Kerne führt zu geänderten Magnetfeldern. Wenn σ B_z der Betrag des am Kern induzierten Sekundärfeldes ist, dann ist das effektive lokale Feld nur B_z(1-σ), die Resonanzfrequenz (Signallage) wird durch die Elektronenhülle der chemischen Bindung unterschiedlich beeinflußt. σ ist ein Tensor 2. Stufe, die chemische Verschiebung ist also anisotrop. In isotropen Medien (Lösungen) verbleibt nur der isotrope Anteil.
Skalare Wechselwirkung: Der Tensor J beschreibt die indirekte Kopplung zweier Kernspins über die Polarisation der Bindungselektronen. Im isotropen Fall bleibt nur die Kopplungskonstante J, die zu den bekannten charakteristischen Aufspaltungsmustern führt und neben der chemischen Verschiebung für die Strukturaufklärung sehr wichtig ist.
Die dipolare Wechselwirkung berücksichtigt die direkte Wechselwirkung von Kernspins bzw. deren magnetischer Momente über den Raum hinweg. Sie tritt nur in anisotroper Umgebung (Festkörper) auf.

Für die Anorganische Chemie ergeben sich im Unterschied zur organischen NMR einige Erweiterungen/Probleme:

Es gibt eine ganze Reihe von Kernen mit einem Kernspin von I > 1/2. Aufgrund der Auswahlregel wird trotz mehrerer vorhandener Niveaus nur ein Signal im Spektrum des jeweiligen Kerns beobachtet. Allerdings bewirken diese Kerne in den Spektren der Nachbarkerne andere Aufspaltungsmuster, statt der n+1-fachen Aufspaltung im I=1/2 Fall, kommt es zu einer 2nI+1-fachen Aufspaltung. Ferner haben diese Kerne ein elektrisches Quadrupolmoment, d.h. die Ladungsverteilung im Kern ist nicht kugelsymmetrisch. Die Folge davon ist eine starke Verkürzung der Spin-Spin-Relaxationszeit T₂ was zu sehr starken Linienverbreiterungen führt. Messungen des Quadrupolmoments sind Gegenstand der NQR-Spektroskopie.
Die in der anorganischen Chemie sehr häufigen paramagnetischen Substanzen bewirken ähnliche Effekte, d.h. es kommt zu sehr starken Linienverbreiterungen. (Die NMR-Spektroskopie ist daher gelegentlich eine einfach Methode um schnell Paramagnetismus festzustellen). Die Untersuchung paramagnetischer Substanzen mittels NMR ist trotzdem nützlich, jedoch keine Routine-Methode.

Apparatives

Die Abbildung I.3.5. zeigt einige Details des 200-MHz- und des neuen 400-MHz-Spektrometers der AC.


Gesamtansicht	Spektrometer	Steuerrechner

Spektrometerunterseite mit Messkopf		Probenröhrchen	Elektronik-Schrank

ausgebauter Messkopf (Gesamtansicht)

Messkopf (Unterseite)		Messkopf (Probenseite)

Gesamtansicht 400 WB	Elektronik-Schrank	Schild	Unterseite 400WB

MAS-Kopf (Unterseite)		Probenwechsler in Aktion
Abb. I.3.5. Fotos des alten 200 MHz-Spektrometers (oben) und des neuen 400 MHz-Spektrometers der Anorganischen Chemie

2. Anorganische Beispiele, Informationen aus verschiedenen Spektrentypen

Aufbauend auf die vorhandenen guten Kenntnisse der Auswertung von ¹H-NMR-Spektern in der organischen Chemie werden im Folgenden mit unterschiedlichen Aufnahmetechniken erhaltene Spektren anorganischer Verbindungen bzgl. der enthaltenen Informationen und Auswertung betrachtet. Auf die zahlreichen Techniken der Aufnahme solcher Spektren kann aus Zeitgründen nicht näher eingegangen werden. Auch für Details (z.B. Daten für chemische Verschiebungen und Kopplungskonstanten einzelner Kerne) muss auf die weiterführende Literatur verwiesen werden.

Einfache, entkoppelte 1-dimensionale Spektren sind sehr einfach auszuwerten. Durch die Breitbandenkopplung ist die chemischen Verschiebung die einzige Information bei entkoppelten Spektren. Wegen der Auswahlregel ΔM_I=±1 sind die Spektren aller Kernen vergleichbar und unabhängig vom Kernspin I. Das Prinzip ist die Abschirmung des äußeren Magnetfeldes B am Kernort durch die Elektronenhüllen der Kerne: Beff.= B0 (1-σ ) Die Abschirmkonstante σ wird relativ zu einem Standard angegeben, so daß die Frequenzabhängigkeit entfällt. Die Größe der chemischen Verschiebung wird i.A. dimensionslos als: δ= Frequenzdifferenz gegen Standard [Hz] Präzessionsfrequenz des Standards [MHz] in der Einheit [ppm] (Parts per Million) angeben.
Als Beispiel zeigt die Abb. I.3.6. (links) das ¹¹B-1D-Spektrum von B₁₀H₁₄. Durch die Breitband-Protonen-Entkopplung treten keine Kopplungen mit den H-Atomen auf. Beobachtet wird direkt die Zahl und die zugehörige chemische Verschiebung symmetrisch verschiedener Kerne. B₁₀H₁₄ enthält vier symmetrisch verschiedene B-Kerne, entsprechend zeigt das Spektrum vier Linien:
- Die vier chemisch gleichen B-Atome (rot) bewirken ein grosses Signal bei δ ca. 0 ppm.
Die drei weiteren Paare von B-Atomen können aus Basis der entkoppelten Spektren nicht unterschieden werden.
- Bei δ = -38 ppm (grün) liegen die B-Atome, die an alle anderen B-Sorten gebunden sind.
- Bei δ = 11 liegen die gelb markierten,
- bei δ = 13 die cyan markierten B-Kerne.
Abb. I.3.6. Spektren von B₁₀H₁₄ (links: Breitband-entkoppeltes 1D-B-NMR-Spektrum; rechts: ) ‣ SVG und ‣ VRML

Die Einflüsse auf die Abschirmung und damit die chemische Verschiebung sind meist nur schwer zu berechnen oder abzuschätzen. Die Abschirmung besteht aus diamagnetischen und paramagnetischen Anteilen; die diamagnetischen werden durch die Elektronendichte im Grundzustand, die paramagnetischen die nur bei nicht s-Orbitalen wichtig sind, auch von angeregten Zuständen beeinflusst. Meist werden Einflüsse der Elektronegativitäten und Oxidationszahlen der Nachbaratome deutlich. Häufig sind auch keine einfachen Abhängigkeiten erkennbar, wie z.B. in ³¹P-Spektren. In diesen Fällen ist dann immer nur ein Vergleich mit Bekanntem (Fingerprint) - wie in der organischen Chemie üblich - sinnvoll.
In nicht entkoppelten 1D-Spektren von I=1/2-Kernen sind die bekannten Kopplungen zwischen den Kernspins beobachtbar. Das Spinsystem A_xB_yC_z zeigt im Spektrum von A (y+1)-Linien mit einer Separation/Kopplung J_AB. Jede Linie ist mit J_AC wieder in (z+1)-Linien gesplittet. Die Intensitätsverhältnisse folgen dem Pascal-Dreieck (inkl. Dacheffekt, bei Spektren höherer Ordnung). Die Größe der Aufspaltung hängt von verschiedenen Faktoren ab:
- vom gyromagnetischen Verhältnis γ beider (!) Kerne.
- nicht vom Magnetfeld.
- der Wechselwirkung der Bindungselektronen mit beiden Kernen.
- der Dipol-Wechselwirkung mit den Elektronen-Spins
- dem sog. Fermi-Kontakt-Term.
Die Einflüsse auf die Auspaltung sind gerade bei anorganischen Verbindungen mit z.T. komplexen Bindungssituationen wieder so vielfältig, dass i.A. mit Vergleichen gearbeitet werden muss.
Als Beispiel zeigt Abb. I.3.7. das ³¹P-Spektrum von PF₂H(¹⁵NH₂)₂. Alle Kerne sind I=1/2-Kerne, d.h. Stickstoff wurde hier zu 100% durch ¹⁵N substituiert ist.

Abb. I.3.7. ³¹P-NMR-Spektrum von PF₂H(¹⁵NH₂)₂ ‣ PDF

Betrachtet man zunächst die größte Kopplungskonstanten (Kerne mit großem γ), dann ergibt sich durch Kopplung mit dem H-Atom ein 1:1-Dublett mit J_PH von 1:2:1-Tripletts mit J_PF. Damit sind die sechs Hauptliniengruppen erklärt. Jede dieser sechs Gruppen ist nochmals 15-fach weiter aufgespalten, denn (durch Kopplung mit zwei N) entsteht ein Triplett mit J_PN von Quintetts (mit J_PH). Insgesamt zeigt das P-Spektrum 2x3x3x5, also 90 Linien.
Die 1D-Spektren von I>1/2-Kernen (Quadrupol-Kerne) haben wegen der Auswahlregel gleiche Form wie die von Kernen mit einer Kernspinquantenzahl von I=1/2. Allerdings sind im Allgemeinen wegen der Quadrupol-Eigenschaften die Feldinhomogenitäten hoch, T₂ ist damit sehr klein und es liegen meist sehr grosse Linienbreiten vor. Zum zweiten bewirken Quadruapol-Kerne bei Spektren der Nachbar-Kerne eine (2nI+1)-fache Aufspaltung der Signale. Als Beispiel ist in Abb. I.3.8. das 1H-Spektrum von German, GeH₄ gezeigt, in dem Ge mit einer Kernspinquantenzahl von I=9/2 ein Splitting im ¹H-Spektrum in 10 Linien (n=1, da nur ein Ge am H gebunden ist, 2nI+1 = 2*1*9/2+1 = 10).

Abb. I.3.8. ¹H-NMR-Spektrum von GeH₄ ‣ PDF
Mit Multi-Puls-Methoden können mit komplizierten Pulsfolgen (vgl. PC) 2D-Spektren usw. aufgenommen werden, mehrere Kerne können also gleichzeitig beobachtet werden. Es können Kopplungen zwischen gleichen/verschiedenen Kernen aufgelöst werden, man spricht dann von sogenannten COSY-Spektren (COrrelated SpectroscopY), entweder von Homo- oder Hetero-COSY-Spektren. Als Beispiel I ist in Abbildung I.3.6 rechts das Homo-(B/B)-COSY-Spektrum von B₁₀H₁₄ schematisch wiedergegeben. Die Signale auf der Diagonalen ergeben nach der Projektion auf die Seiten das normale 1D-¹¹B-Spektrum. Die Cross-Peaks außerhalb der Diagonalen zeigen die Kopplung zwischen den jeweiligen Kernen an. Bei Boranen speziell findet man starke Kopplungen zwischen direkt gebundenen B-Atomen, jedoch nicht in den Fällen, in denen die beiden B-Atome von mit einer H-Brücke überbrückt sind. Dieses Spektrum ermöglichen jetzt für das Beispiel B₁₀H₁₄ eine vollständige Zuordnung:
- Aus den Intensitäten wird sofort klar, daß der Peak bei ca. 1 ppm den vier rot gekennzeichneten B-Kernen zugeordnet werden kann.
- Die gelb markierten B-Atome (bei 11 ppm) koppeln nur mit den grün markierten (nur dort gibt es Off-Diagonal-Intensität)
- Die grün markierten B-Kerne sind mit allen anderen verbunden und gekoppelt, d.h. es kann sich bei diesen nur um das Signal bei -37 ppm handeln.
Das Beispiel II zeigt in Abbildung I.3.9. das Hetero-¹¹B/¹H-COSY-Spektrum des gleichen Borans.

Abb. I.3.9. Spektrum von B₁₀H₁₄ ‣ SVG

in der die starken Kopplungen von B mit den direkt gebundenen exo-H-Atomen deutlich wird. Die Spektren (a) (links) sind mit Protonenenkopplung aufgenommen, die Protonen und ihre Zuordnung zu den jeweiligen B-Atomen sind direkt sichtbar, Brücken-H-Atome (schwarz) werden nicht sichtbar. Im Spektrum (b) (rechts) ohne Protonenentkopplung sind die Brücken-H-Atome schwach, es wird erkennbar, mit welchen B-Atomen sie verknüpft sind.

3. Festkörper-NMR (MAS-NMR)

Das Problem bei der Aufnahme von Festkörper-Pulverspektren ist die starke Linienverbreiterung durch die magnetische Anisotropie im Festkörper. Die Wechselwirkungen ist nicht mehr durch ein Skalar zu beschreiben, es liegen Tensor-Eigenschaften vor, die im Laborsystem (je nach Symmetrie) mit bis zu neun Komponenten (3x3-Tensor) berücksichtigt werden müssen. Dieser Tensor kann in ein Hauptachsensystem (Ellipsoid) transformiert werden. Obwohl jeder Kristallit eine andere Orientierung im Feld einnimmt, mitteln sich diese Effekt im Pulver nicht aus.

Abb. I.3.9. Prinzip der MAS-NMR ‣ SVG

Die Spektren zeigen eine sehr breite Resonanz mit Grenzwerten, die den Extrema der Hauptachsenelemente des Tensors entsprechen. Wird die Probe allerdings in einem Rotor im magischen Winkel 54.7^o zum Feld sehr schnell rotiert, dann können alle anisotropen Effekte ausgemittelt werden und man erhält 'normale' Spektren auch von Festkörpern. Die Wechselwirkungen F_iso liegen bei 1/3 der Spur des orthogonalisierten F-Tensors. Die Vermessung einzelner Tensorelemente ist selbstverständlich möglich, wenn es gelingt einen ausreichend großen Einkristall mit einem Goniometer im Spektrometer zu orientieren (KEINE Routinemethode).

Abb. I.3.10. Spektrum von B₁₀H₁₄ ‣ SVG

Als Beispiel für ein MAS-NMR-Spektrum ist in Abbildung I.3.11. das ²⁹Si-COSY MAS-NMR-Spektrum von Dodecasil-1H (auch ZSM-39 genannt) dargestellt, in dem die drei Sorten (A, B, C) von Si (wenige A, sehr viele C) und deren Verknüpfung (A nicht mit C verknüpft) deutlich werden. Besonders wichtig ist die FK-NMR für die Ermittlung der Al/Si-Verteilung und deren Verknüpfung in Alumosilicaten.