| cr_home | Metalle | Nichtmetalle | FK-Chemie | Strukturchemie | Interm. Phasen | Oxide | Silicate | Strukturtypen | AFP |
| ← | Inhalt | Einleitung | I. Spektroskopie | II. Beugung | III. Bildgebung | IV. Sonstige Methoden | → |
Vorlage(n)
| cos α | sin α | 0 |
| -sin α | cos α | 0 |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | -1 |
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
|---|---|---|---|---|
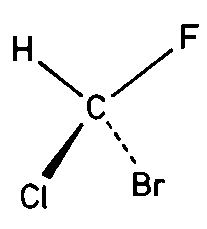
| Cs | m |
 |
 |
 |
| Ca8B18O33Cl4 4 H2O |
| -1 | 0 | 0 |
| 0 | -1 | 0 |
| 0 | 0 | -1 |
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
|---|---|---|---|---|
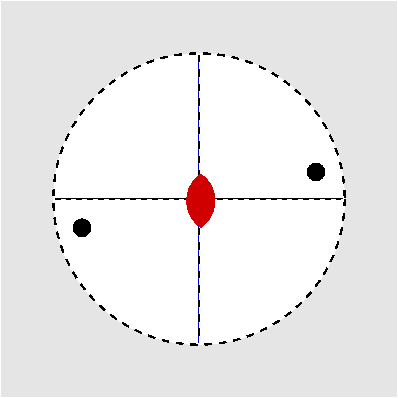
| Ci | -1 |
 |
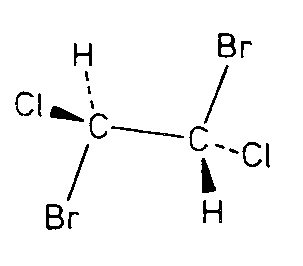 |
 |
| MnSiO3 |
| C4 | i |
|---|---|
 |
 |
| Achse | n=1 | n=2 | n=3 | n=4 | n=6 |
|---|---|---|---|---|---|
| Dreh- | S1 | S2 | S3 | S4 | S6 |
| spiegel-A. | σ | i | C3h | ||
| Sn |
 |
 |
 |
 |
 |
| Dreh- | -1 | -2 | -3 | -4 | -6 |
| inversions-A. | i | m | 3+i | 3/m | |
| -n |
 |
 |
 |
 |
 |
|
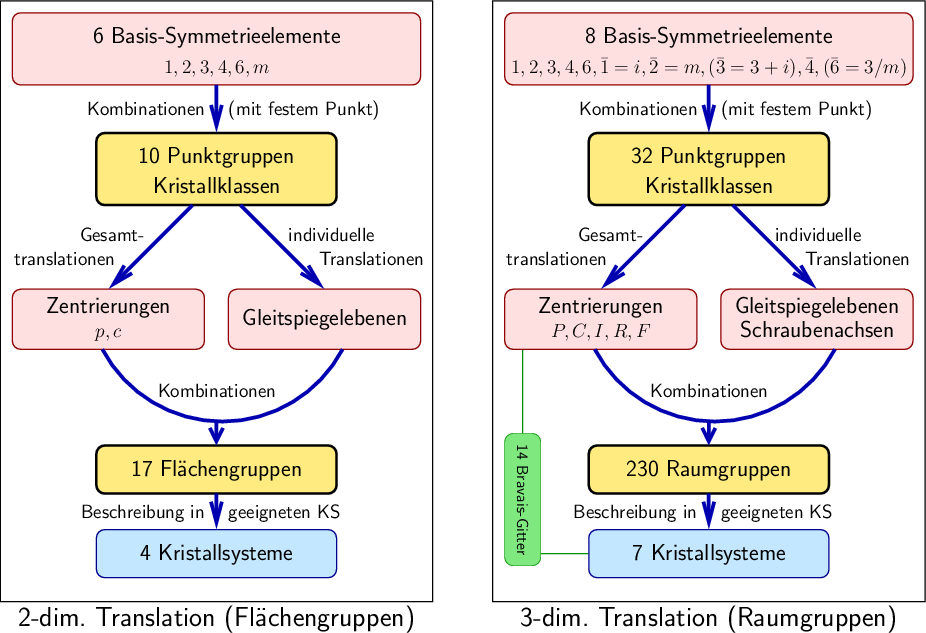
| Abb. I.6.1. Flächen- und Raumgruppen ‣ SVG |
| Nr. | Hermann-Mauguin | Schönflies | Koordinatensystem |
|---|---|---|---|
| 1 | 1 | C1 | schiefwinklig: a ≠ b, γ beliebig |
| 2 | 2 | C2 | |
| 3 | 1m1 | Cm | rechtwinklig: a ≠ b, γ=90o |
| 4 | 2mm | C2v | |
| 5 | 411 | C4 | quadratisch: a=b, γ=90o |
| 6 | 4mm | C4v | |
| 7 | 311 | C3 | hexagonal a=b, γ=120o |
| 8 | 3m1 | C3v | |
| 9 | 611 | C6 | |
| 10 | 6mm | C6v |
| Nr. | Hermann-Mauguin- | Schönflies- | Name | Koordinatensystem | |
|---|---|---|---|---|---|
| Kurz-Symbol | Lang-Symbol | Symbol | (Mineralogie) | ||
| 1 | 1 | 1 | C1 | triklin-pedial | triklin (keine ausgezeichnete Richtung): a, b, c beliebig; α, β, γ, beliebig |
| 2 | -1 | -1 | Ci | triklin-pinakoidal | |
| 3 | m | 1m1 | Cs | monoklin-domatisch | monoklin (eine ausgezeichnete Richtung, die üblicherweise als b-Richtung gewählt wird): a ≠ b, γ beliebig |
| 4 | 2 | 121 | C2 | monoklin-sphenoidisch | |
| 5 | 2/m | 12/m1 | C2h | monoklin-prismatisch | |
| 6 | mm2 | mm2 | C2v | rhombisch pyramidal | orthorhombisch: a ≠ b ≠ c; α=β=γ=90o |
| 7 | 222 | 222 | D2 | rhombisch-dispheniodisch | |
| 8 | mmm | 2/m 2/m 2/m | D2h | rhombisch-dipyramidal | |
| 9 | 4 | 411 | C4 | tetragonal-pyramidal | tetragonal: a=b≠c, α=β=γ=90o |
| 10 | -4 | -4 | S4 | tetragonal-disphenoidisch | |
| 11 | 4/m | 4/m | C4h | tetragonal-dipyramidal | |
| 12 | 4mm | 4mm | S4 | ditetragonal-pyramidal | |
| 13 | -42m | -42m | C4h | tetragonal-skalenoedrisch | |
| 14 | 422 | 422 | S4 | tetragonal-trapezoedrisch | |
| 15 | 4/mmm | 4/m 2/m 2/m | D4h | ditetragonal-dipyramidal | |
| 16 | 3 | 3 | C3 | trigonal-pyramidal | trigonal, (hexagonale Achsen): a=b≠c, α=β=90o |
| 17 | -3 | -3 | S6 | rhomboedrisch | |
| 18 | 3m1 | 3m1 | C3v | ditrigonal-pyramidal | |
| 19 | 321 | 321 | D3 | ditrigonal-trapezoedrisch | |
| 20 | -3m1 | -3 2/m 1 | D3d | ditrigonal-skalenoedrisch | |
| 21 | 6 | 6 | C6 | hexagonal-pyramidal | hexagonal: a=b≠c; α=β=90o, γ=120o |
| 22 | -6 | -6 | C3h | trigonal-dipyramidal | |
| 23 | 6/m | 6/m | C6v | hexagonal-dipyramidal | |
| 24 | -6m2 | -6m2 | D3h | ditrigonal-dipyramidal | |
| 25 | 6mm | 6mm | C6v | dihexagonal-pyramidal | |
| 26 | 622 | 622 | D6 | hexagonal-trapezoedrisch | |
| 27 | 6/mmm | 6/m 2/m 2/m | D6h | dihexagonal-dipyramidal | |
| 28 | 23 | 23 | T | tetraedrisch-pentagondodekaedrisch | kubisch: a=b=c, α=β=γ=90o |
| 29 | m-3 | 2/m -3 | Th | disdodekaedrisch | |
| 30 | -43m | -4 3 m | Td | hexakistetraedrisch | |
| 31 | 432 | 432 | O | pentagonikositetraedrisch | |
| 32 | m-3m | 4/m -3 2/m | Oh | hexakisoktaedrisch | |
|
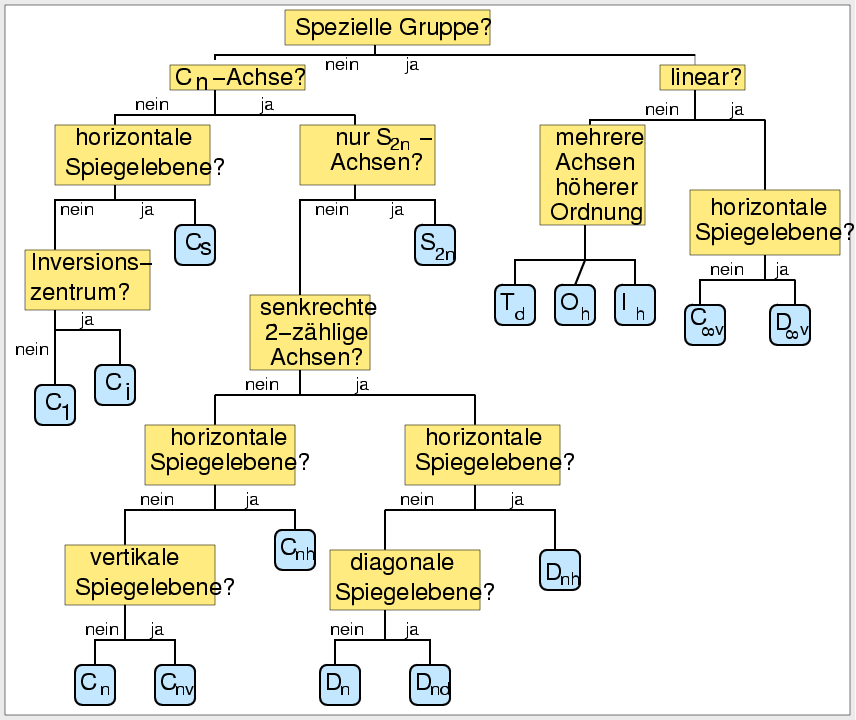
| Abb. I.6.2. Fließschema zur Bestimmung der Punktgruppe ‣ SVG |
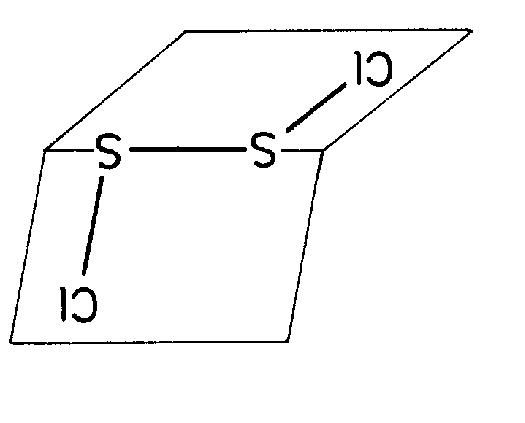
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
|---|---|---|---|---|
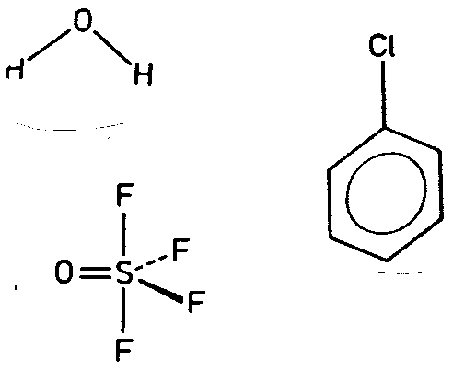
| C2v | 2 mm |
 SVG
SVG |
 |
 |
| Mg(NH4)PO4 6 H2O | ||||
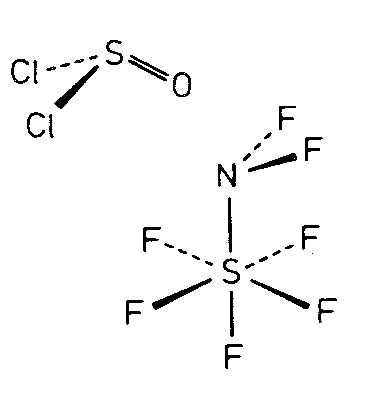
| H2O (2mm): Molekül alleine und mit SE | ||||
| SO2Cl2 (2mm) Molekül alleine und mit SE | ||||
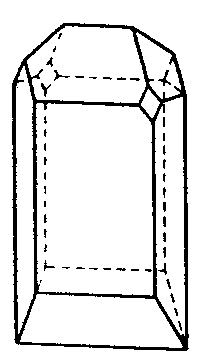
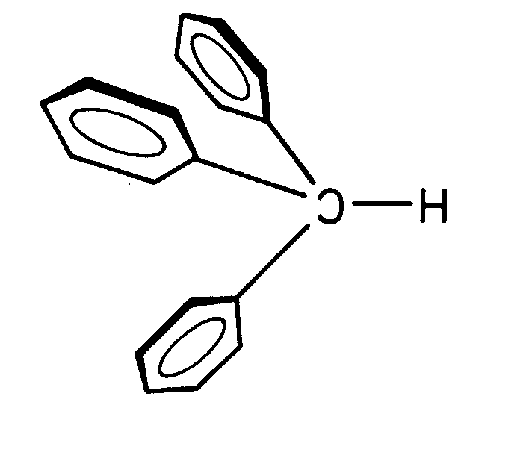
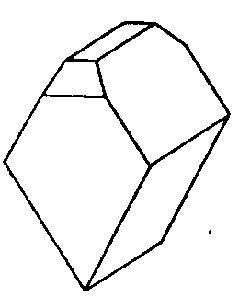
| C3v | 3 m |
 SVG
SVG |
 |
 |
| Turmalin | ||||
| C4v | 4 m m |
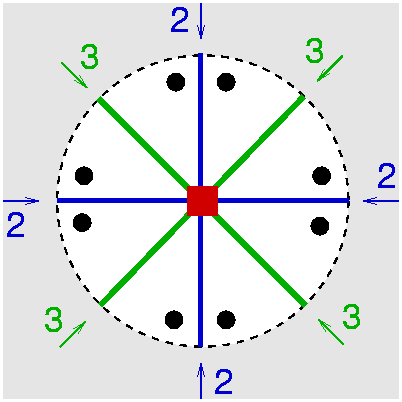 SVG
SVG |
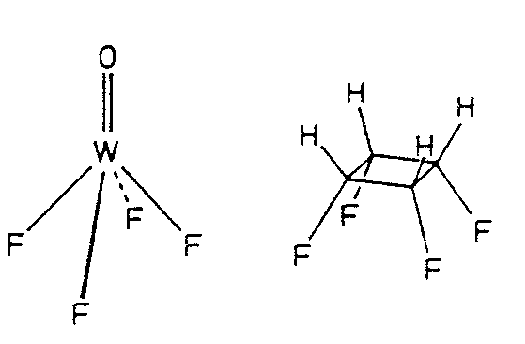 |
 |
| AuS(CH2C6H5)2Cl | ||||
| C5v | - |
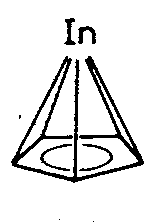 |
||
| C6v | 6 m m |
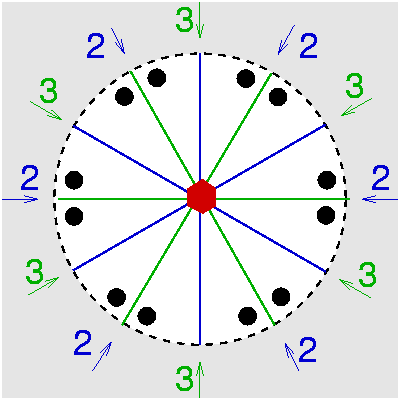 SVG
SVG |
 |
 |
| Bromellit (BeO) |
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
|---|---|---|---|---|
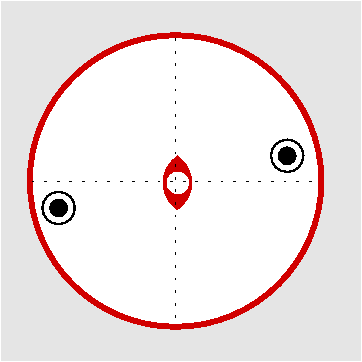
| C2h | 2/m |
 SVG
SVG |
 |
 |
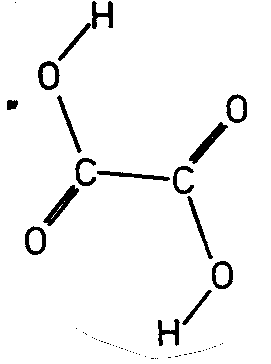
| BaS2O6 2 H2O | ||||
| Oxalsäure C2O4H2: (2/m) Molekül alleine und mit SE | ||||
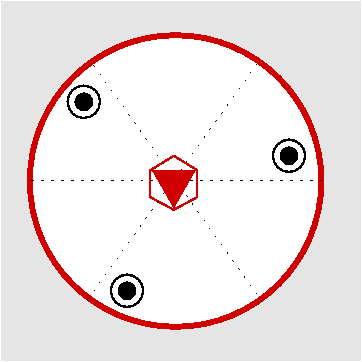
| C3h | 3/m= -6 |
 SVG
SVG |
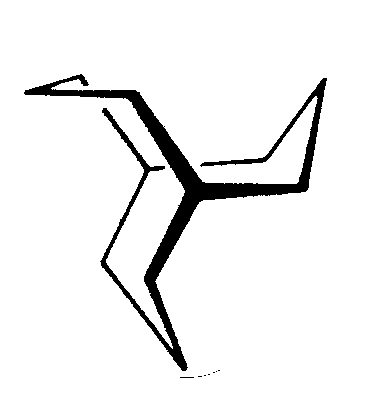 |
 |
| Li2O2 | ||||
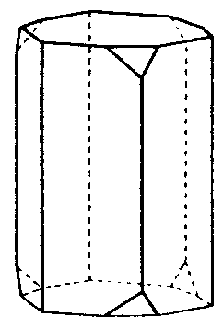
| C4h | 4/m |
 SVG
SVG |
 |
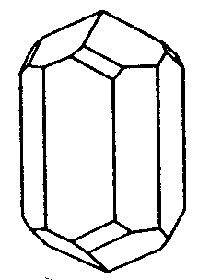 |
| Na4Al3Si9O24Cl (Meionit) | ||||
| C6h | 6/m |
 SVG
SVG |
 |
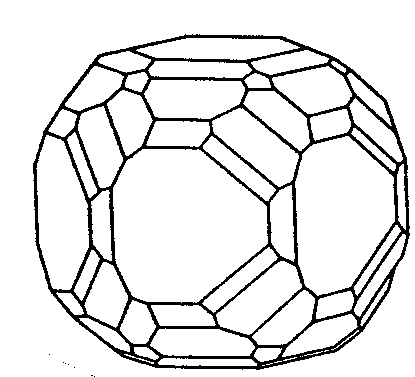 |
| Ca5(PO4)3F (Apatit) |
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
|---|---|---|---|---|
| D2 | 2 2 2 |
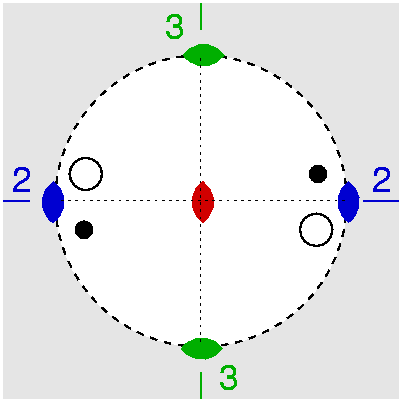 SVG
SVG |
 |
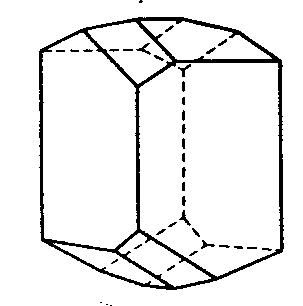 |
| Ba(HCOO)2 | ||||
| Twistan (222) Molekül mit SE | ||||
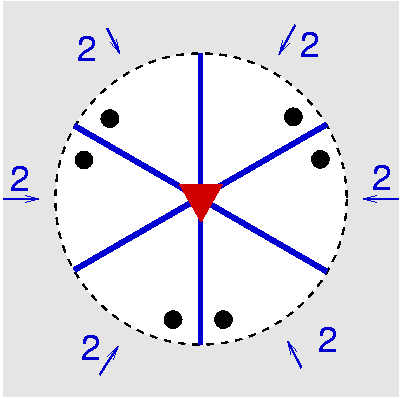
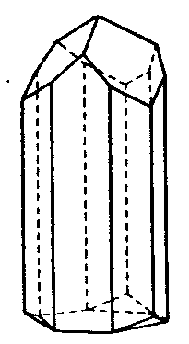
| D3 | 3 2 |
 SVG
SVG |
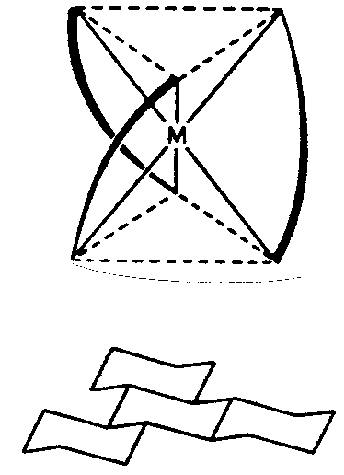 |
 |
| Tris-chelat-Komplexe (32) Molekül | ||||
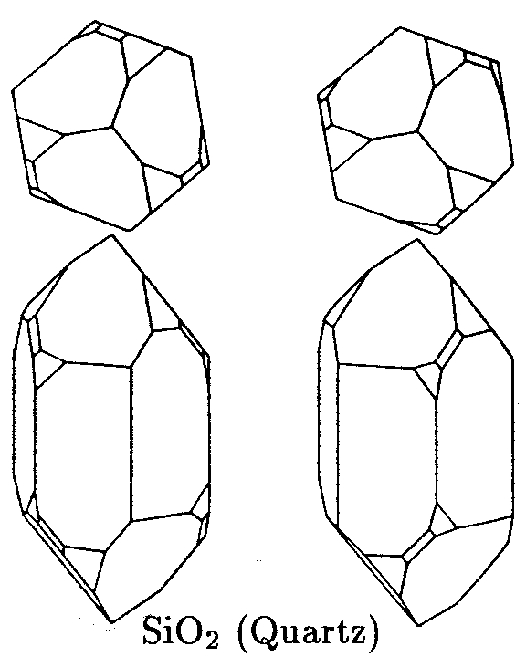
| D4 | 4 2 2 |
 SVG
SVG |
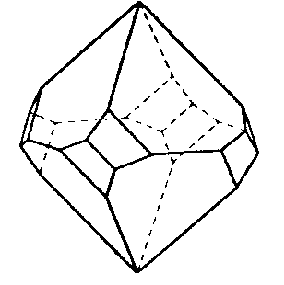 |
|
| Cl3CCO2K . Cl3CCO2H | ||||
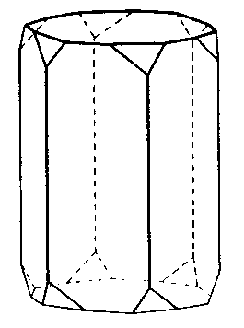
| D6 | 6 2 2 |
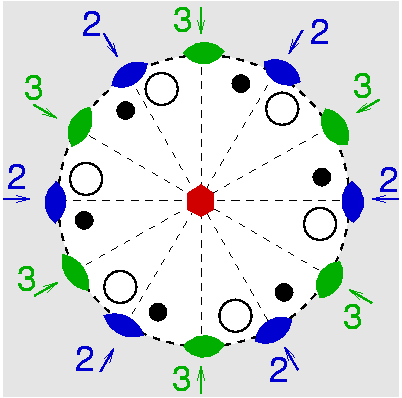 SVG
SVG |
 |
|
| SiO2 (Quarz) |
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
|---|---|---|---|---|
| D2h | m m m |
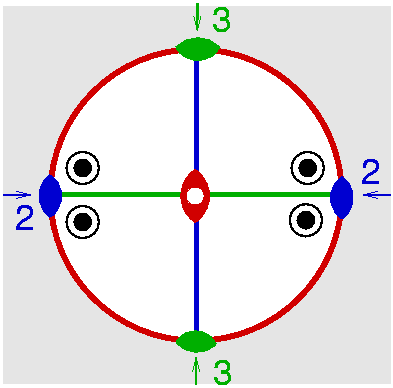 SVG
SVG |
 |
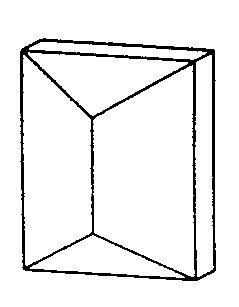 |
| HFeAl5Si2O13 (Staurolit) | ||||
| D3h | -6 2 m |
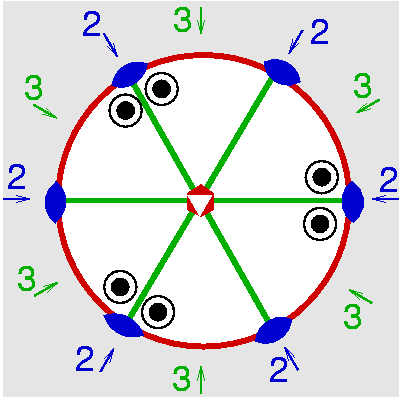 SVG
SVG |
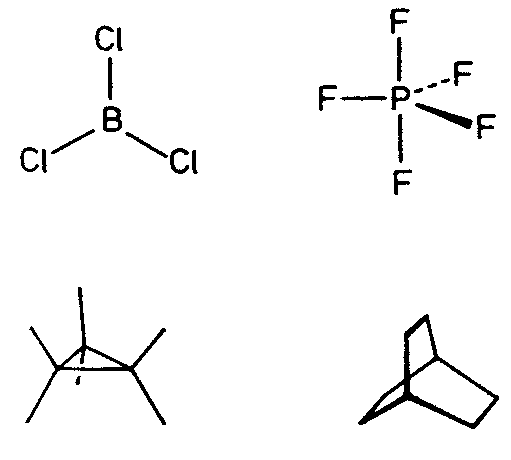 |
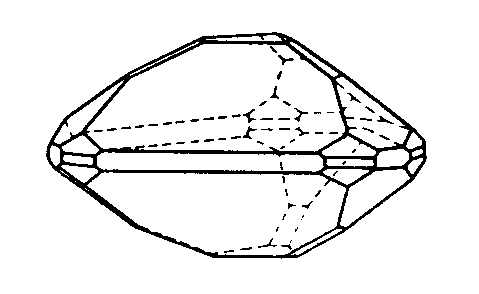 |
| BaTiSi3O9 | ||||
| D4h | 4/mmm = 4/m2/m2/m |
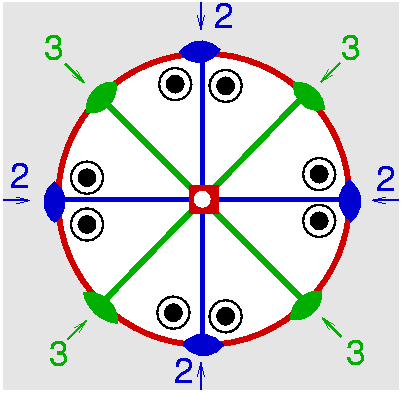 SVG
SVG |
 |
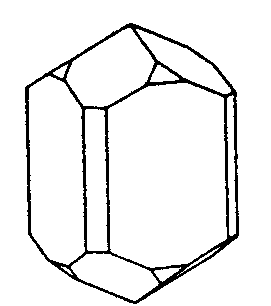 |
| TiO2 (Rutil) | ||||
| Re2(CO)10: Molekül alleine, mit 4/m in z, mit 2/m in x, mit 2/m in d und mit allen SE | Rutil: Kristall alleine, mit 4/m in z, mit 2/m in x, mit 2/m in d und mit allen SE | |||
| D5h | - |
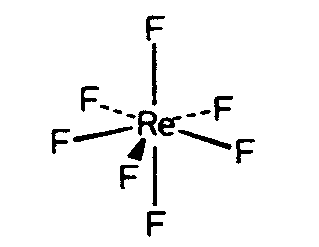 |
||
| D6h | 6/m 2/m 2/m |
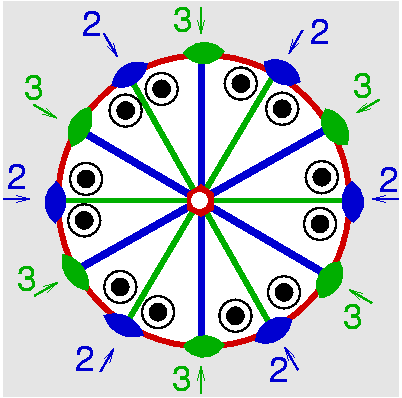 SVG
SVG |
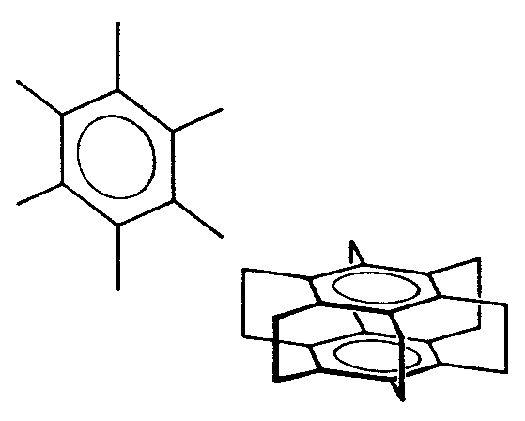 |
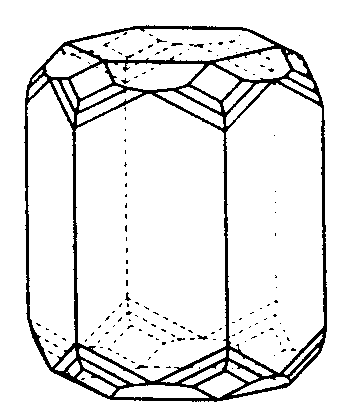 |
| Be3Al2Si6O18 | ||||
| D∞h | - | O=C=O, H-H |
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
|---|---|---|---|---|
| D2d | -4 2 m |
 SVG
SVG |
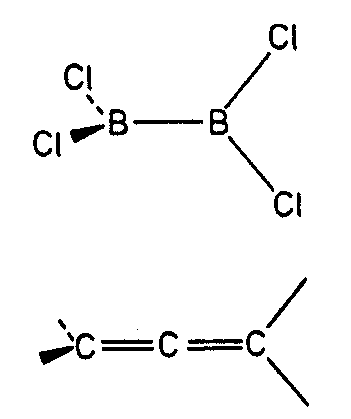 |
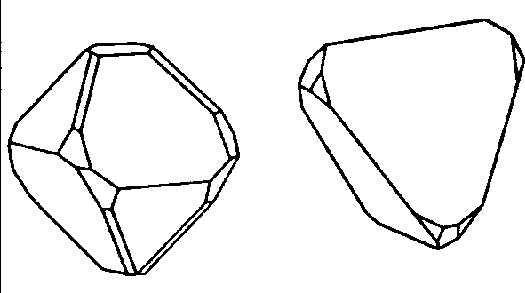 |
| CuFeS2 (Chalkopyrit) | ||||
| D3d | -3 m = -3 2/m |
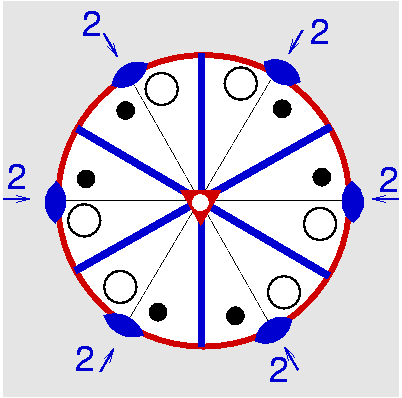 SVG
SVG |
 |
 |
| CaCO3 (Calcit) | ||||
| D4d | - |
 |
||
| Mn2(CO)10: Molekül alleine, mit 4/m in z, mit 2/m in x, mit 2/m in d und mit allen SE | ||||
| D5d | - |
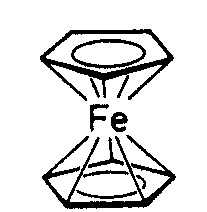 |
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
|---|---|---|---|---|
| S4 | -4 |
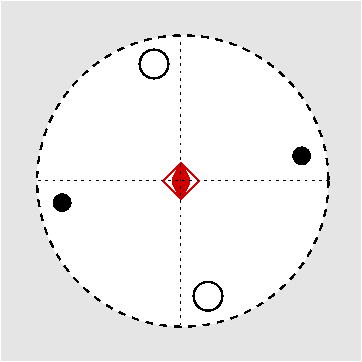 SVG
SVG |
 |
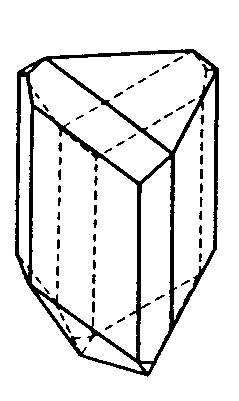 |
| CaB(OH)4AsO4 (Cahnit) | ||||
| S6 | -3 |
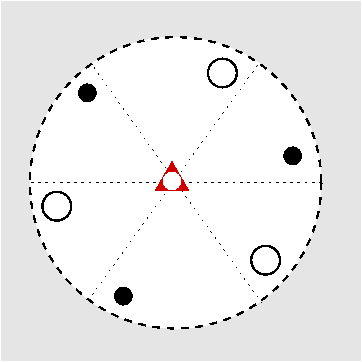 SVG
SVG |
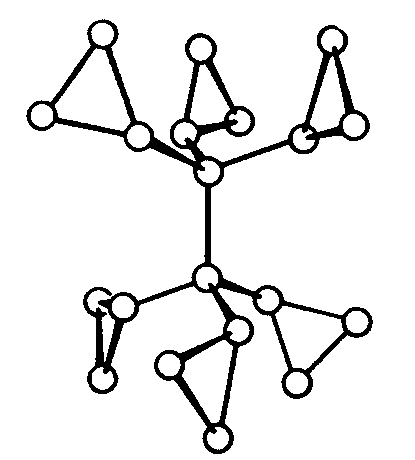 |
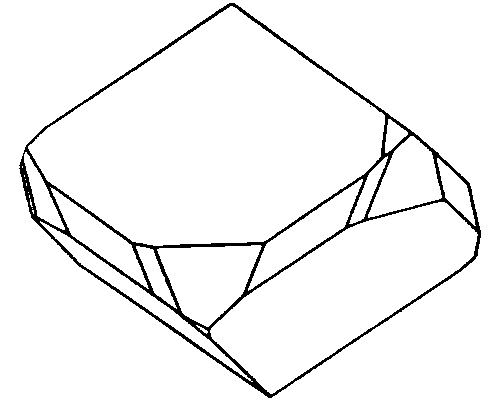 |
| CaMg(CO3)2 |

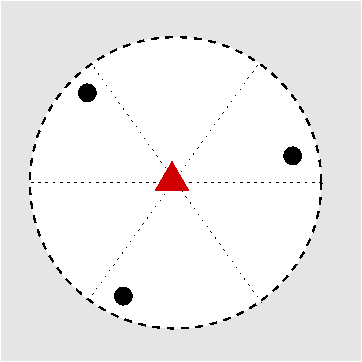
|
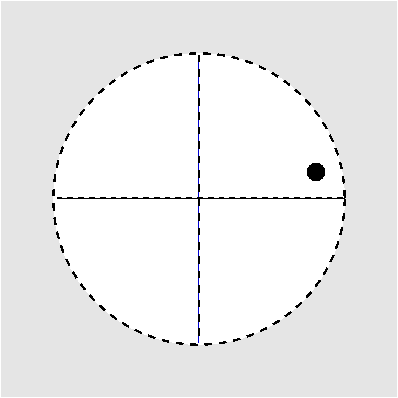
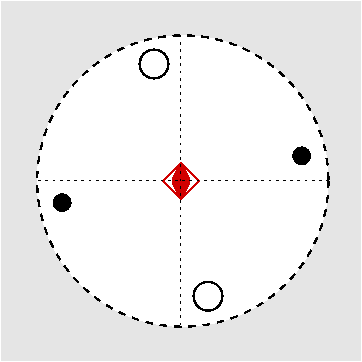
| Abb. I.6.3. Prinzip der stereographischen Projektion ‣ SVG |
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
|---|---|---|---|---|
| T | 23 |
 SVG
SVG |
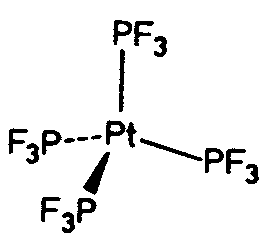 |
 |
| NaClO3 | ||||
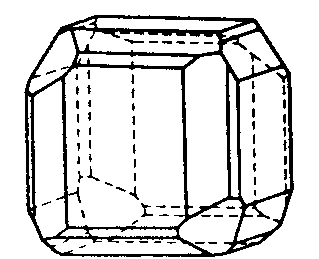
| Th | 2/m -3 = m -3 |
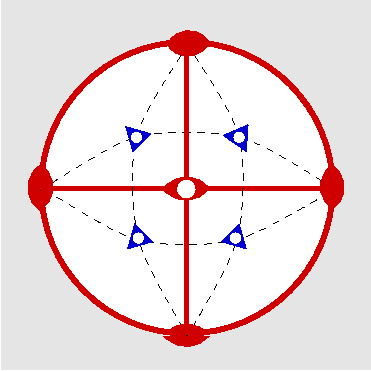 SVG
SVG |
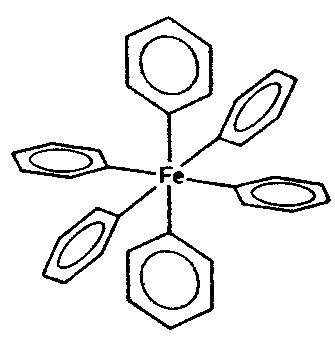 |
 |
| FeS2 (Pyrit) | ||||
| Td | -4 3 m |
 SVG
SVG |
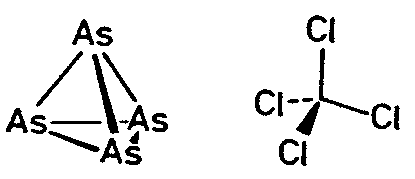 |
 |
| ZnS (Sphalerit) | ||||
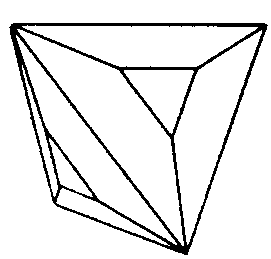
| O | 432 |
 SVG
SVG |
 |
|
| Cu2O | ||||
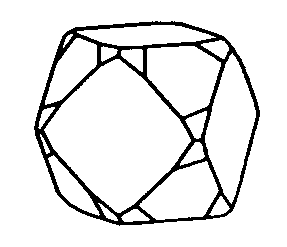
| Oh | 4/m -3 2/m = m -3 m = m 3 m |
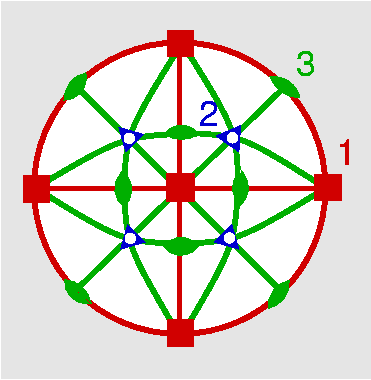 SVG
SVG |
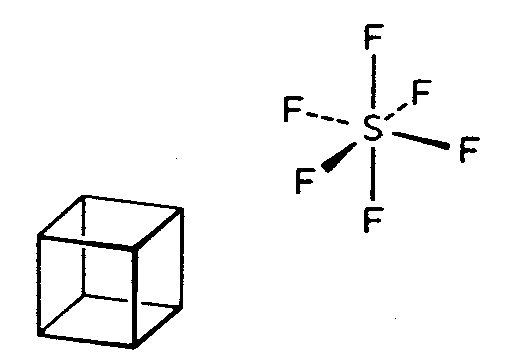 |
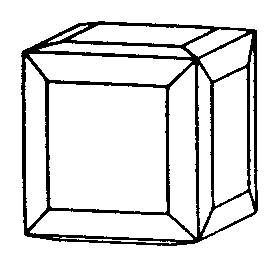 |
| Cu |
| Zähnigkeit | Summenformel | Isomer A1 | Isomer A2 | Isomer B1 | Isomer B2 | Isomer C |
|---|---|---|---|---|---|---|
| einzähnig | MA6 | MA6 (Oh,m3m) | ||||
| MA5B | MA5B(C4v,4mm) | |||||
| MA4B2 | cis(C2v,2mm) | trans(D4h,4/mmm) | ||||
| MA3B3 | fac(C3v,3m1) | mer(C2v,2mm) | ||||
| MA2B2C2 | cis/cis/cis(C1,1) | cis/cis/cis(C1,1) | cis/cis/trans(C2v,2mm) | trans/trans/trans(D2h,mmm) | ||
| zweizähnig | M(AA)3 | A1 (D3,32) | A2 (D3,32) | |||
| ein- und zweizähnig | M(AA)2B2 | A1 (C2,2) | A2 (C2,2) | B (D2h,mmm) | ||
| ein- und vierzähnig | M(AAAA)B2 | A1(C2,2) | A2(C2,2) | B1(C1,1) | B2(C1,1) | C(C2v,2mm) |
| Anwendung | Basis |
|---|---|
| Zahl/Symmetrie von Molekülschwingungen (3N, mit Gesamttranslation/-libration) | kartesische Verschiebungsvektoren |
| Zahl/Symmetrie von Molekülschwingungen (3N-6, d.h. ohne Gesamttranslation/-libration, Normalkoordinatenanalyse) | interne Verschiebungskooordinaten |
| Konstruktion von MO's | Atomorbitale |
| Ligandenfeldtheorie | d-Atomorbitale |
| Konstruktion von Hybridorbitalen | Positionvektoren, die auf die Liganden zeigen |
| Voraussage erlaubter chemischer Reaktionen | Molekülorbitale |
| Charaktere unter der Symmetrieoperation | ||||
|---|---|---|---|---|
| Symmetrieoperation | E | C2 | σv(xz) | σv(yz) |
| Translation parallel z | 1 | 1 | 1 | 1 |
| Translation parallel x | 1 | -1 | 1 | -1 |
| Translation parallel y | 1 | -1 | -1 | 1 |
| Rotation um z | 1 | 1 | -1 | -1 |
| Rotation um x | 1 | -1 | -1 | 1 |
| Rotation um y | 1 | -1 | 1 | -1 |
| Mulliken-Symbol | E | C2 | σv(xz) | σv(yz) | Vektoren | Tensoren |
|---|---|---|---|---|---|---|
| A1 | 1 | 1 | 1 | 1 | z | x2, y2, z2 |
| A2 | 1 | 1 | -1 | -1 | Rz | xy |
| B1 | 1 | -1 | 1 | -1 | x, Ry | xz |
| B2 | 1 | -1 | -1 | 1 | y, Rx | yz |
| Dimension der Darstellung | Charakter bei | Symbole | ||||
|---|---|---|---|---|---|---|
| E | Cn | i | σh | σv oder C2 | ||
| 1 | 1 | 1 | A, a | |||
| 1 | -1 | B, b | ||||
| 2 | 2 | E, e | ||||
| 3 | 3 | T, t | ||||
| 1 | g (gerade, tiefgestellt) | |||||
| -1 | u (ungerade, tiefgestellt) | |||||
| 1 | ' (einfach gestrichen) | |||||
| -1 | '' (doppelt gestrichen) | |||||
| 1 | 1 (tiefgestellt) | |||||
| -1 | 2 (tiefgestellt) | |||||
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| Mulliken-Symbol | E | C2 | σv(xz) | σv(xz) | Rechnung nach Formel |
|---|---|---|---|---|---|
| reduzible Darstellung | 3 | 1 | 1 | 3 | Spuren der Matrizen |
| A1 | 1 | 1 | 1 | 1 | 1/4 [3*1 + 1*1 + 1*1 + 3*1] = 2 |
| A2 | 1 | 1 | -1 | -1 | 1/4 [3*1 + 1*1 + 1*(-1) + 3*-1] = 0 |
| B1 | 1 | -1 | 1 | -1 | 1/4 [3*1 + 1*(-1) + 1*1 + 3*-1] = 0 |
| B2 | 1 | -1 | -1 | 1 | 1/4 [3*1 + 1*(-1) + 1*(-1) + 3*1] = 1 |
| Kontrollrechnung | 2+1 =3 | 2-1 =1 | 2-1 =1 | 2+1 =3 | Ergebnis: 2 A1 + 1 B2 |

|
| Abb. I.6.4. Interne Normalschwingungen des Wassermoleküls ‣ SVG |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | -1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | -1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| Mulliken-Symbol | E | C2 | σv(xz) | σv(xz) | Rechnung nach Formel XY |
|---|---|---|---|---|---|
| reduzible Darstellung | 9 | -1 | 1 | 3 | Spuren der Matrizen |
| A1 | 1 | 1 | 1 | 1 | 1/4 [9*1 + (-1)*1 + 1*1 + 3*1] |
| A2 | 1 | 1 | -1 | -1 | 1/4 [9*1 + (-1)*1 + 1*(-1) + 3*(-1)] |
| B1 | 1 | -1 | 1 | -1 | 1/4 [9*1 + (-1)*(-1) + 1*1 + 3*(-1)] |
| B2 | 1 | -1 | -1 | 1 | 1/4 [9*1 + (-1)*(-1) + 1*(-1) + 3*1] |
| Kontrollrechnung | 3+1+2+3 = 9 | 3+1-2-3 = -1 | 3-1+2-3 = 1 | 3-1-2+3 =3 | 3 A1 + A2 + 2 B1 + 3 B2 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1s(H1) | |
| 0 | 1 | 0 | 0 | 0 | 0 | 1s(H2) | |
| 0 | 0 | 1 | 0 | 0 | 0 | 2s(O) | |
| 0 | 0 | 0 | 1 | 0 | 0 | 2pz(O) | |
| 0 | 0 | 0 | 0 | 1 | 0 | 2px(O) | |
| 0 | 0 | 0 | 0 | 0 | 1 | 2py(O) |
| 0 | 1 | 0 | 0 | 0 | 0 | 1s(H1) | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1s(H2) | |
| 0 | 0 | 1 | 0 | 0 | 0 | 2s(O) | |
| 0 | 0 | 0 | 1 | 0 | 0 | 2pz(O) | |
| 0 | 0 | 0 | 0 | -1 | 0 | 2px(O) | |
| 0 | 0 | 0 | 0 | 0 | -1 | 2py(O) |
| 0 | 1 | 0 | 0 | 0 | 0 | 1s(H1) | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1s(H2) | |
| 0 | 0 | 1 | 0 | 0 | 0 | 2s(O) | |
| 0 | 0 | 0 | 1 | 0 | 0 | 2pz(O) | |
| 0 | 0 | 0 | 0 | 1 | 0 | 2px(O) | |
| 0 | 0 | 0 | 0 | 0 | -1 | 2py(O) |
| 1 | 0 | 0 | 0 | 0 | 0 | 1s(H1) | |
| 0 | 1 | 0 | 0 | 0 | 0 | 1s(H2) | |
| 0 | 0 | 1 | 0 | 0 | 0 | 2s(O) | |
| 0 | 0 | 0 | 1 | 0 | 0 | 2pz(O) | |
| 0 | 0 | 0 | 0 | -1 | 0 | 2px(O) | |
| 0 | 0 | 0 | 0 | 0 | 1 | 2py(O) |
| Mulliken-Symbol | E | C2 | σv(xz) | σv(xz) | Rechnung nach Formel XY |
|---|---|---|---|---|---|
| reduzible Darstellung | 6 | 0 | 2 | 4 | Spuren der Matrizen |
| A1 | 1 | 1 | 1 | 1 | 1/4 [6*1 + 0*1 + 2*1 + 4*1] = 3 |
| A2 | 1 | 1 | -1 | -1 | 1/4 [6*1 + 0*1 + 2*(-1) + 4*(-1)] = 0 |
| B1 | 1 | -1 | 1 | -1 | 1/4 [6*1 + 0*(-1) + 2*1 + 4*(-1)] = 1 |
| B2 | 1 | -1 | -1 | 1 | 1/4 [6*1 + 0*(-1) + 2*(-1) + 4*1] = 2 |
| Kontrollrechnung | 3+1+2 = 6 | 3-1-2 = 0 | 3+1-2 = 2 | 3-1+2 = 4 | 3 a1 + 1 b1 + 2 b2 |
| H-Atom-Gruppenorbitale | O-Atomorbitale | |
|---|---|---|
| (aus RR 2 0 0 2 für die beiden 1s-AO von H) | ireduzible Darstellung | (O auf allen SE -> AO haben Symmetrieeigenschaften einer IR) |
| PHI = s1 + s2 | a1 | 2s, 2pz |
| a2 | ||
| b1 | 2px | |
| PHI = s1 - s2 | b2 | 2py |

|
| Abb. I.6.X. MO-Schema von Wasser. ‣ SVG |
| ← | Inhalt | Einleitung | I. Spektroskopie | II. Beugung | III. Bildgebung | IV. Sonstige Methoden | → |
| cr_home | Metalle | Nichtmetalle | FK-Chemie | Strukturchemie | Interm. Phasen | Oxide | Silicate | Strukturtypen | AFP |