


| <<<< Symmetrie | <<<< Methoden |
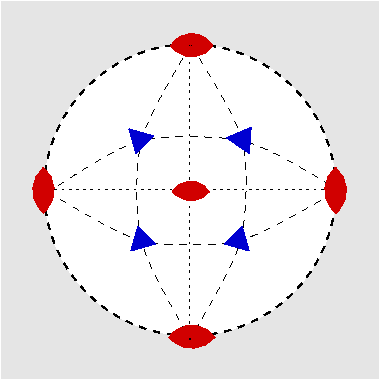
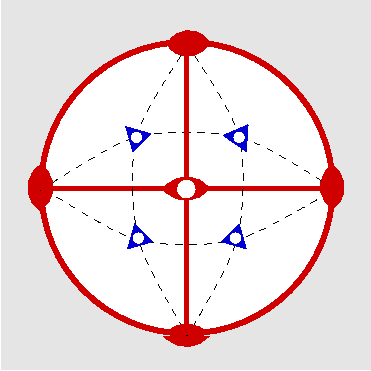
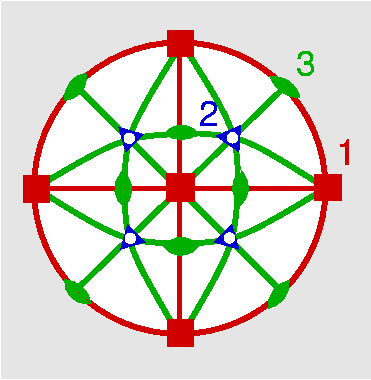
| Schönflies | H.M. | stereographische Projektion | Molekül | Kristall |
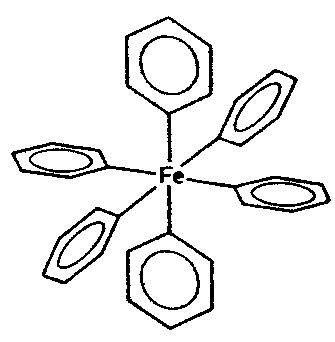
| T | 23 |
 |
 |
 |
| NaClO3 | ||||
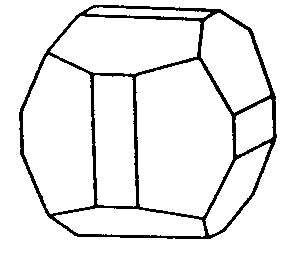
| Th | 2/m -3 = m -3 |
 |
 |
 |
| FeS2 (Pyrit) | ||||
| Td | -4 3 m |
 |
 |
 |
| ZnS (Sphalerit) | ||||
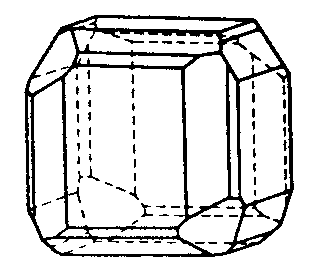
| O | 432 |
 |
 |
|
| Cu2O | ||||
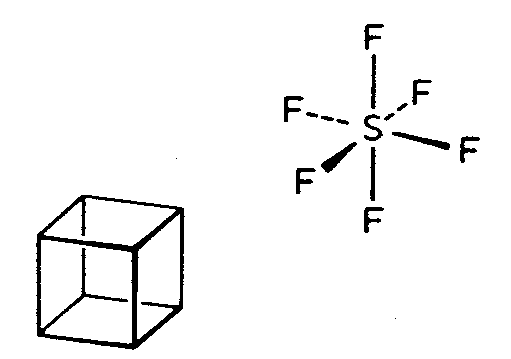
| Oh | 4/m -3 2/m = m -3 m = m 3 m |
 |
 |
 |
| Cu |
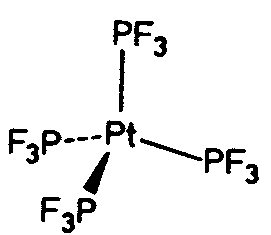
| Zähnigkeit | Summenformel | Isomer A1 | Isomer A2 | Isomer B1 | Isomer B2 | Isomer C |
| einzähnig | MA6 | MA6 (Oh,m3m) | ||||
| MA5B | MA5B(C4v,4mm) | |||||
| MA4B2 | cis(C2v,2mm) | trans(D4h,4/mmm) | ||||
| MA3B3 | fac(C3v,3m1) | mer(C2v,2mm) | ||||
| MA2B2C2 | cis/cis/cis(C1,1) | cis/cis/cis(C1,1) | cis/cis/trans(C2v,2mm) | trans/trans/trans(D2h,mmm) | ||
| zweizähnig | M(AA)3 | A1 (D3,32) | A2 (D3,32) | |||
| ein- und zweizähnig | M(AA)2B2 | A1 (C2,2) | A2 (C2,2) | B (D2h,mmm) | ||
| ein- und vierzähnig | M(AAAA)B2 | A1(C2,2) | A2(C2,2) | B1(C1,1) | B2(C1,1) | C(C2v,2mm) |
| <<<< Symmetrie | <<<< Methoden |