|
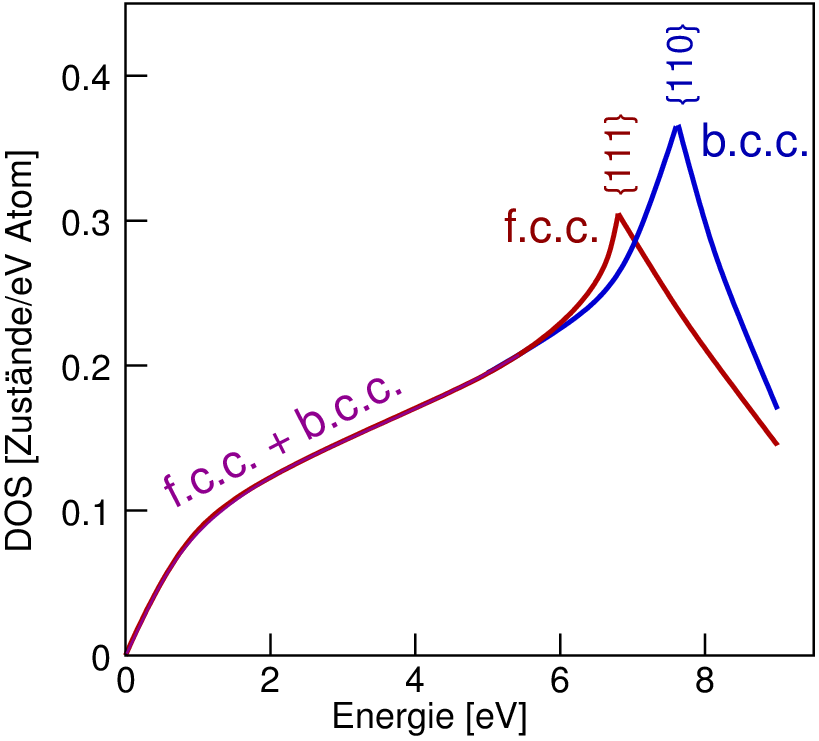
| Abb. 4.3.1. Schematischer Verlauf der DOS im f.c.c. und im b.c.c.-Gitter ‣SVG |
| cr_home | Metalle | Nichtmetalle | Strukturchemie | Festkörperchemie | Oxide | Silicate | Strukturtypen |
| ⇦ | Inhalt | Kap. 1 | Kap. 2 | Kap. 3 | Kap. 4 | Kap. 5 | Kap. 6 | Kap. 7 | Kap. 8 | Lit. | ⇨ |
| α-Phase | β-Phase | γ-Phase | ε-Phase | |
| Struktur | f.c.c. | b.c.c. | γ-Messing | h.c.p. |
| VEC (nach Hume-Rothery) | - | 3/2=21/14=1.5 | 21/13=1.615 | 7/4=1.75 |
| max. Löslichk. (nach Mott + Jones) | 1.362 | 1.48 | 1.538 | |
| experimentelle Werte | ||||
| Cu-Zn | (1.284) | CuZn (1.48) | Cu5Zn8 (1.58-1.66) | CuZn3 |
| Cu-Sn | (1.270) | Cu4Sn (1.49) | Cu31Sn8 (1.67) | Cu3Sn |
| Cu-Al | (1.408) | Cu3Al (1.48) | Cu9Al4 (1.62-1.77) | |
| Co-Zn | CoZn3 | Co5Zn21 | - | |
| Cu-In | Cu3In | Cu9In4 | - | |
| Rh-Zn | - | Rh5Zn21 | - |
Die Abhängigkeit der Phasenfolge bei bestimmten Legierung von der Valenzelektronenkonzentration wurde 1928 von Hume-Rothery entdeckt. 1936 gelang Mott und Jones die Erklärung der Stabilitätsfolgen mit dem einfachen 'Nearly Free Elektron' Ansatz. Danach sollen die f.c.c.- und die b.c.c.-Struktur bis zu der Elektronenkonzentration stabil, bis zu der die Fermikugel die 1. Brillouin-Zone berührt. Diese Grenzen sind 1.36 Elektronen/Atom für das f.c.c. und 1.48 Elektronen/Atom für die b.c.c.-Packung. Bei jeweils höheren Werten für die VEC soll danach eine neue Struktur ausgebildet werden, bei der die Fermikugel noch nicht die Wände der 1. BZ berührt.

|
| Abb. 4.3.1. Schematischer Verlauf der DOS im f.c.c. und im b.c.c.-Gitter ‣SVG |
Mit Bandstrukturrechnungen auf aktuellem DFT-Niveau lassen sich die Phasenfolgen mittlerweile befriedigend aus den elektronischen Strukturen erklären. Dabei ist zu beachten und wichtig, dass sich die Brillouin-Zone mit dem Strukturtyp ändert.
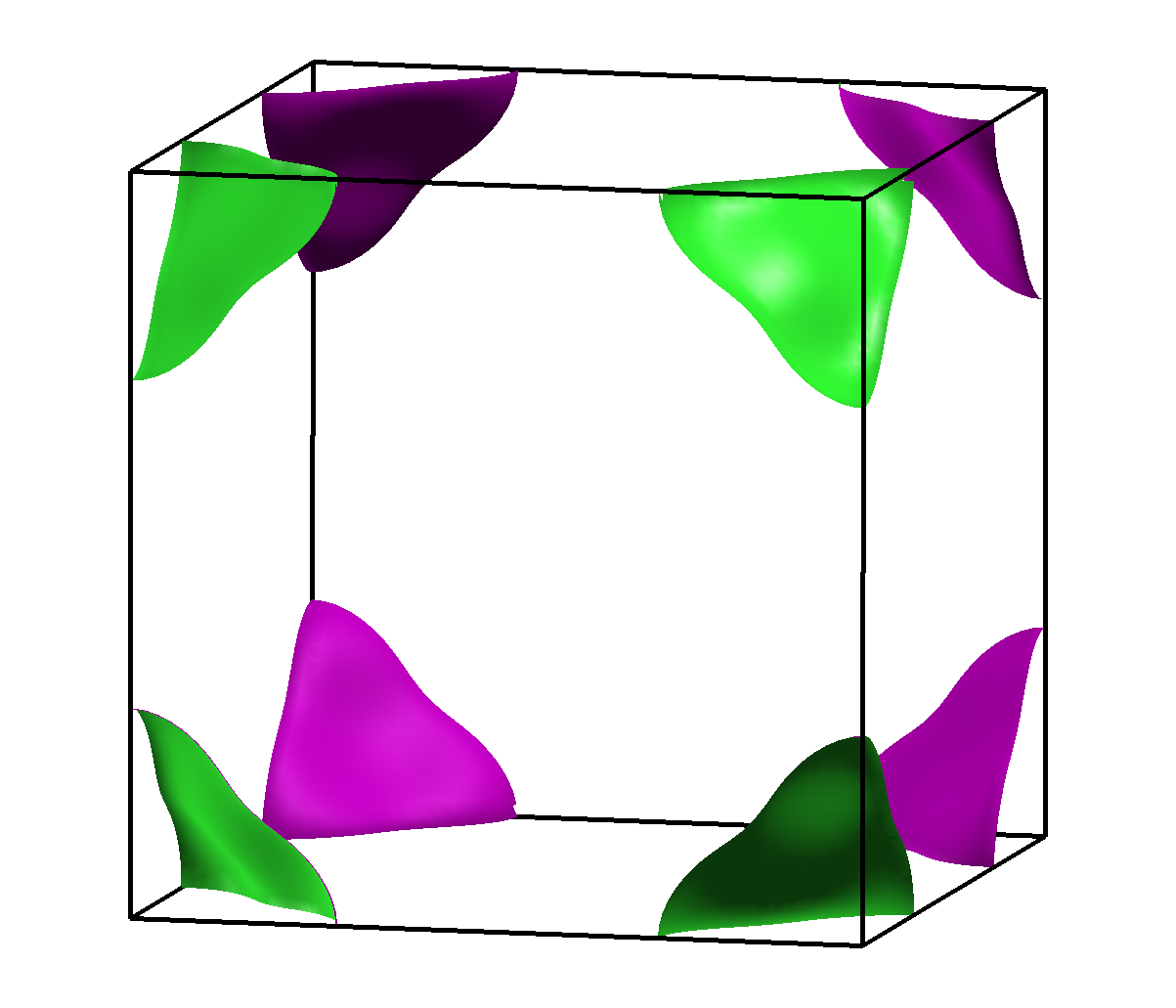
|
|
| Abb. 4.3.2. Fermiflächen in β-Messing (FP-LAPW-Rechnung, 1000 k-Punkte, PBE-GGA-Funktional) | |
Die DOS selber weicht erheblich vom NFE-Fall ab (Abb. 4.3.3.). Man erkennt jedoch das für reine Metalle ungewöhnliche Minimum der tDOS etwas oberhalb der beobachteten Elektronenkonzentration.
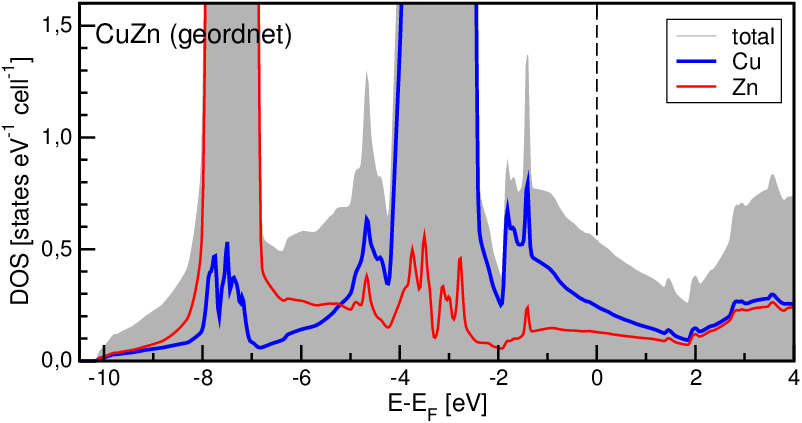
|
| Abb. 4.3.3. Totale und partielle Zustandsdichten der geordneten β-Messing-Phase CuZn ‣SVG |
|
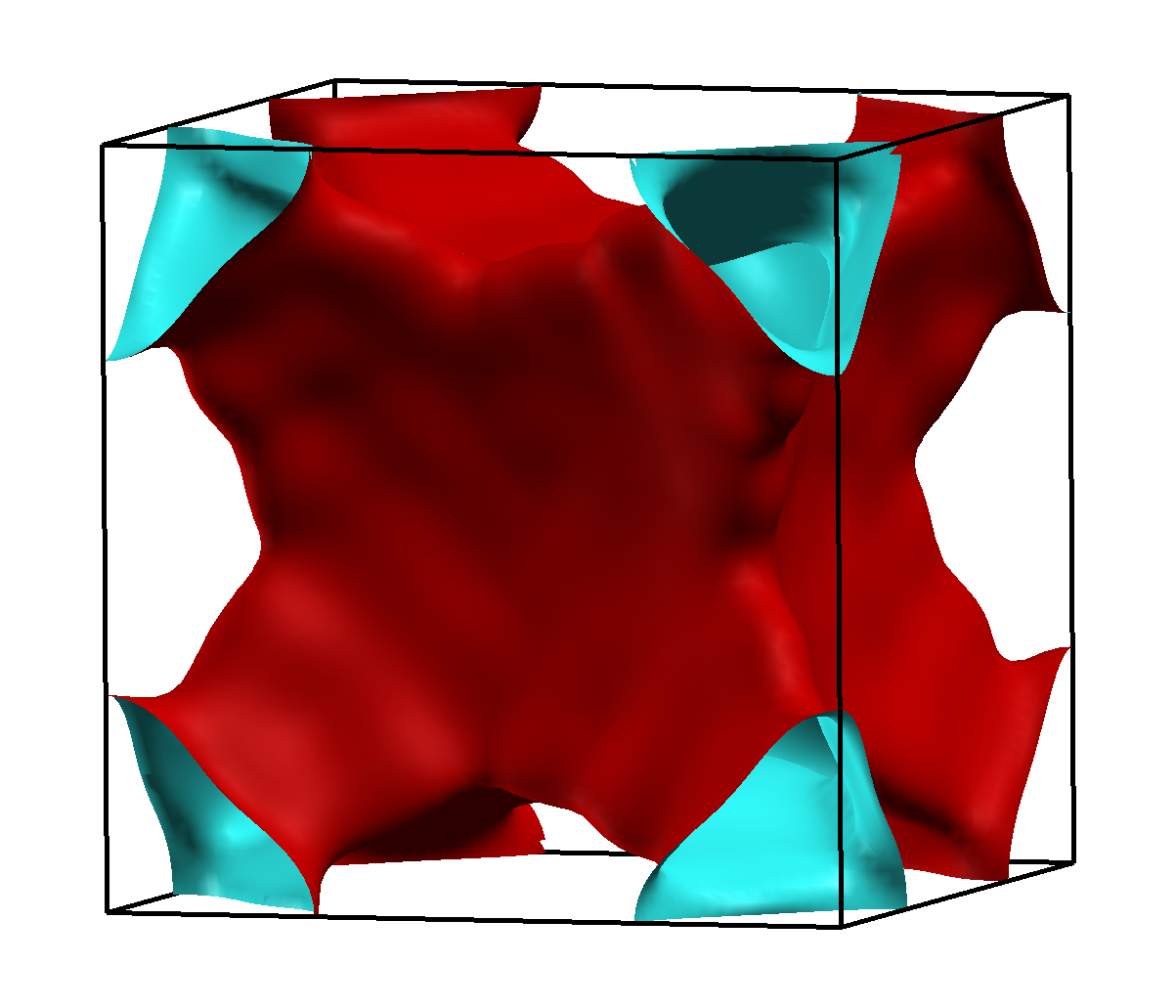
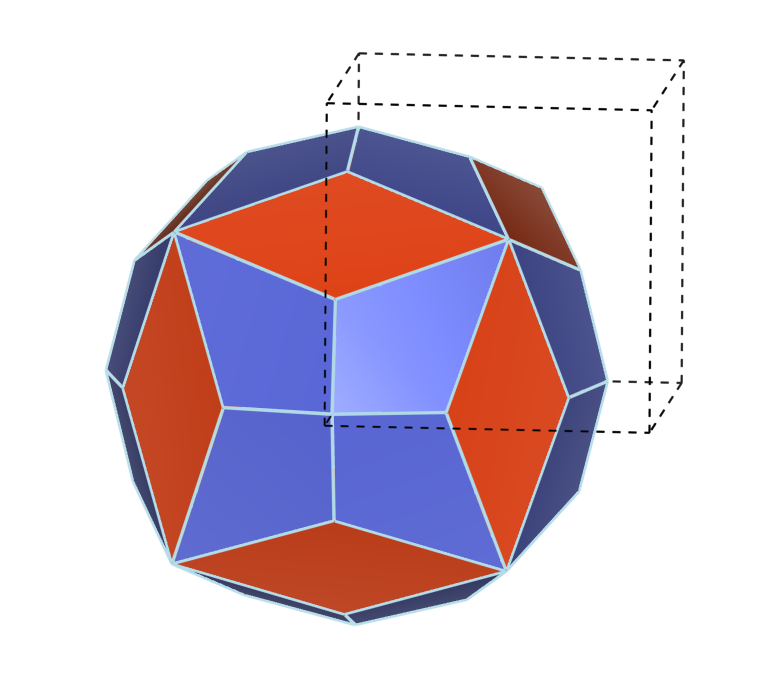
| Abb. 4.3.4. Jones-Zone von γ-Messing, gebildet aus den Flächen {330} (rot) und {411} (blau) der kubisch-innenzentrierten Elementarzelle. |
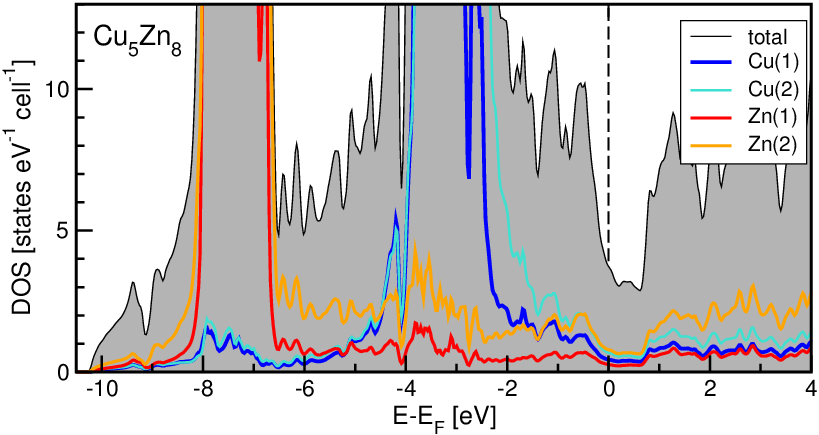
Damit geht sehr deutlich (s. Abb. 4.3.5.) eine extrem gut ausgeprägte Pseudobandlücke einher.
|
| Abb. 4.3.5. Totale und partielle Zustandsdichten der geordneten γ-Messing-Phase Cu5Zn8 ‣SVG |
| ⇦ | Inhalt | Kap. 1 | Kap. 2 | Kap. 3 | Kap. 4 | Kap. 5 | Kap. 6 | Kap. 7 | Kap. 8 | Lit. | ⇨ |
| cr_home | Metalle | Nichtmetalle | Strukturchemie | Festkörperchemie | Oxide | Silicate | Strukturtypen |