1. Generelles zur Spektroskopie

Vorlage zu I.1.

• Vorlage I-1.1: Spektrometer - Spektrum (allgemein) (PS, PDF)

Bei allen spektrokopischen Methoden wird die Proben elektromagnetischer Strahlung ausgesetzt. Gemessen werden die dann die "Anderungen der Energien/Wellenl"angen dieser Strahlung. Nach dem Welle -- Teilchen-Dualismus handelt es sich bei dieser elektromagnetischen Strahlung entweder um eine Welle, deren Energie nach den bekannten Gesetzm"assigkeiten mit der Wellenl"ange bzw. Frequenz zusammenh"angt: E = h $\nu$ = h $\frac{c}{\lambda}$ = h c $\tilde{\nu}$} In Energie (E = h $\nu$ (in [eV] oder [J/mol] wird daher in den entsprechenden Einheiten angegeben:

• $\nu$ Frequenz in Hertz ($s^{-1}$) (h=Plancksches Wirkungsquantum: 6.63 $10^{-34}$ Js (Wirkung!)
• $\lambda$ Wellenl"angen: E = h $\nu$ = h $\frac{c}{\lambda}$ (wegen $\nu = \frac{c}{\lambda}$) (c=3 $10^8$ m/s)
• $\tilde{\nu}$ Wellenzahl: E = h $\nu$ = h $\frac{c}{\lambda}$ = h c $\tilde{\nu}$ (wegen $\tilde{\nu} = \frac{1}{\lambda}$)

• monochromatisch/polychromatisch ($\lambda$ = E =... Verteilung) (s.u.)
• koh"arent/nicht koh"arent (alle Wellen in Phase) z.B. Laser f"ur RAMAN
• polarisiert: alle E-Feldvektoren in gleicher Orientierung $\star$ ORD: optische Rotationsdispersion (Quelle: linear polarisiert) (nach Ausrichtung im Magnetfeld: MORD!) $\star$ CD: Circular-Dichroismus (Quelle: zirkular polarisiert) $\mapsto$ beide: Spezialmethoden f"ur chirale Infos

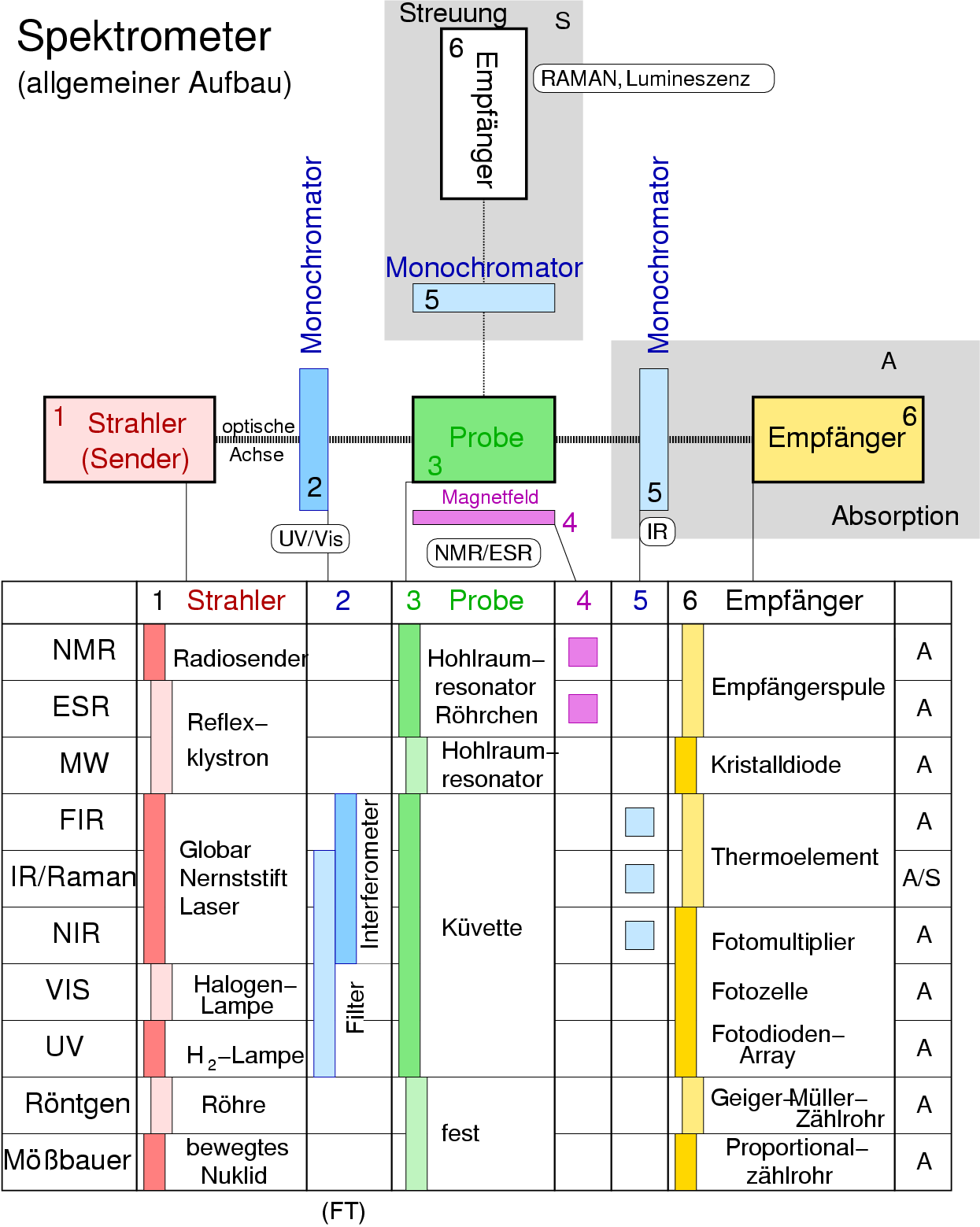Abb. I.1.1. Spektrometer (allgemein, schematisch) ‣SVG

• Strahler, Sender, Quelle (je nach E, s.u.)
• (Monochromator: Gitter, Interferometer, Prisma, Filter)
• Probe (fest, fl"ussig, gas)
• Detektoren (je nach E)

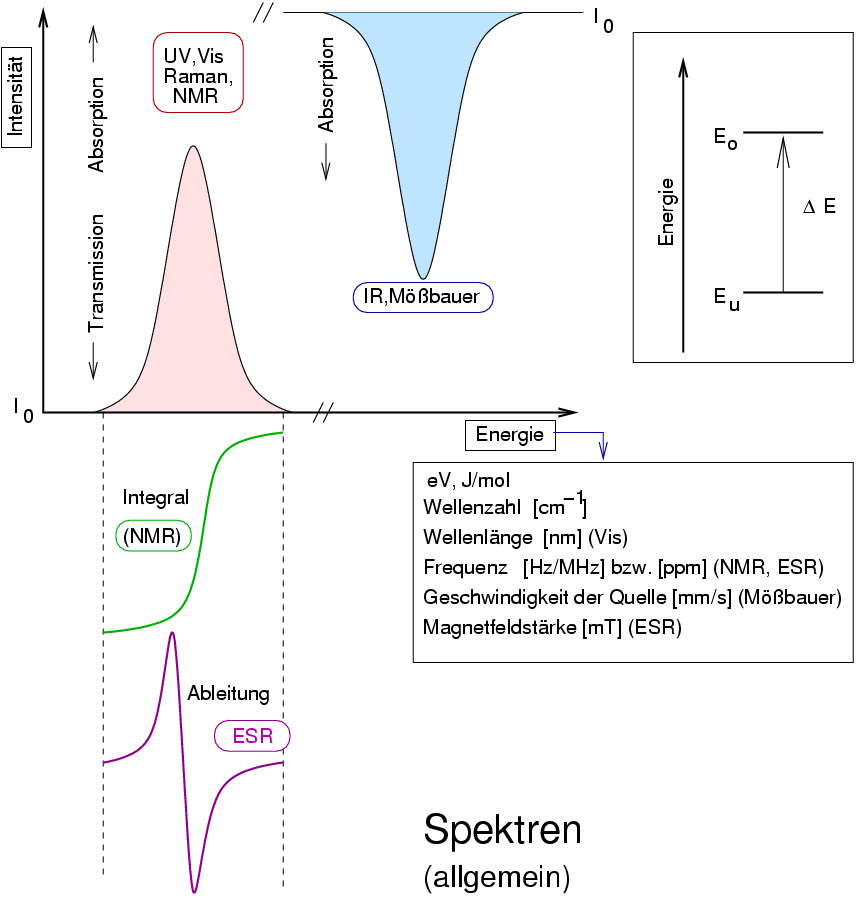Abb. I.1.2. Spektrum (allgemein, schematisch) ‣ SVG

• Bei der Emissions-Spektroskopie ist die Probe selber die Quelle. Bekannt ist das Prinzip von der Flammenf"arbung (aus dem Analytik-Praktikum) oder der AES (aus der Analytik-II-Vorlesung).
• Am h"aufigsten wird Absorptions-Spektroskopie (Symbol A in Abb. I.1.1.) betrieben. Verwendet werden dabei wei"se oder monochromatische Quellen. Messgro"se ist die Intensit"at-Verteilung (d.h. ohne die absorbierten Energien). Der Effekt ist bekannt aus dem sichtbaren Spektralbereich, sichtbar ist immer die zur emmittierenten Strahlung analoge Komplement"arfarbe.
• Bei den Streuung-Methoden (Symbol S in Abb. I.1.1.) befindet sich der Dektektor nicht auf optischer Achse sondern senkrecht dazu, detektiert wird also nur die Streustrahlung. Die bekanntest Methode hierzu ist die RAMAN-Streuung.

• Erw"armung der Probe
• Streuung in alle Raumrichtungen (auch beobachtbar: z.B. Raman)
• Ausl"osen chemischer Prozesse (z.B. Molek"uldissozisation)
• Fluoreszenz (andere Wellenl"angen werden emittiert)

Energien/Einheiten/Methoden/Quellen

• NMR ("Anderung des Kernspins) und ESR ("Anderung des Elektronenspins)
  • E: Frequenz [MHz] oder Magnetfeldst"arke [T] (da die Energie vom zus"atzlich anliegendem Magnetfeld abh"angt)
  • Q: (Radio)-Sender (monochromatisch) oder Klystron (monochromatisch)
• MW Molek"ul-Rotationen (nur Gase)
  • E: Wellenzahl [cm^{-1}]
  • Q: Klystron (monochromatisch)
• IR/Raman Molek"ulschwingungen
  • E: Wellenzahl [cm^{-1}]
  • Q: Nernststift, Globar (polychr.) Laser (monochrom. f"ur RAMAN)
• UV/VIS $e^-$-Anregung
  • E: $\lambda$ in nm
  • Q: VIS: Halogen-Lampe; UV: Wasserstoff-Lampe
• UPS/XPS (UV bzw. R"ontgen-Photo-$e^-$-Sp.) Anregung von Valenz-$e^-$ durch R"ontgen/UV-Strahlung
  • E: Energie [eV]
  • Q: R"ontgenr"ohre
• Bei der M"o"sbauer-Spektroskopie erfolgt die Anregung mit Kernenergien:
  • Q: radioaktiver $\gamma$-Strahler
  • E: eigene Skala wg. Dopplereffekt, E in [mm/s]

Spektrum <--> quantenmechanisches System

• E: Eigenenergien $\Leftarrow$ Gesucht!
• H: Operator der Energie (Rechenvorschrift, wie aus Ortskoordinaten die entsprechende klassische Gleichung wird)
• \psi$: Eigenfunktion (f"ur Spektro: meistens nur Symmetrie wichtig)
• x: 3 N Koordinaten der Teilchen + ev. Spin (real: ziemlich viele!)

• {Mikrowellen = Rotationen} der Gesamtmolek"ule einfachstes Modell: starrer Rotator H: $E_{kin.}$ von Rotation E-Lsg.: $E=BJ(J+1)$ mit $B=\frac{h}{8 \pi^2 I c}$ und $I=\mu r_0^2$ Auswahlregel: $\Delta J = \pm 1$ (2,6,12,20,..) Spektrum: alle 2B eine Linie (2,4,6,...)
• IR/Raman = interne Schwingungen} Modell: harmonischer Oszillator H: $E_{kin.}$ + $E_{Hook}$ E-Lsg: $E_v=h \nu (v+\frac{1}{2})$ Auswahlregel: $\Delta v= \pm 1$ Spektrum: eine Linie, da alle E "aquidistant
• UV/VIS = $e^-$-"Uberg"ange} in Atomen/Molek"ulen Modell I: H-Atom: H: $E_{kin.}$ + $E_{pot.}$ von $e^-$ am Proton E-Lsg: $E_n = - \frac{R}{n^2}$ (mit R=Rydbergkonstante 13.6 eV) Auswahlregel: $\Delta$ n beliebig Spektrum: $\mapsto$ bekanntes Spektrum immer enger liegender Linien (z.B. Lyman-Serie) $\mapsto$ komplizierte Molek"ule: MO = LCAO

Intensit"aten

1. Probendicke (d) und Konzentration (c) nach Lambert-Beer: \fbox{$I = I_0 10^{-\epsilon c d}$} $\epsilon$ = Extinktionskoeffizient I im Spektrum als: Transmission: $\frac{I}{I_0} = T$ Absorption: A = 1-T auch Integrale oder differenziert (s.o.) $\Downarrow$ f"ur $\epsilon$ aus Quantenmechanik $\Downarrow$ \ding{193} \underline{Besetzungen der Zust"ande} Verteilung der Teilchen auf den verschiedenen Niveaus im GG Boltzmann-Verteilung: \fbox{$\frac{N_{oben}}{N_{unten}} = e^{\frac{-\Delta E}{kT}}$} !! kT in E-Skala !!: kleines E $\mapsto$ fast Gleichverteilung zwischen o und u $\mapsto$ sehr geringe Intensit"aten ($\mapsto$ "au"seres H-Feld n"otig) ab IR h"ohere Intensit"at wegen wenige populiertem o-Zustand mit Tricks auch Besetzungsumkehr
2. "Ubergangswahrscheinlichkeit \underline{genau:} komplizierte Quantenmechanik (St"orungstheorie) L"osung der zeitabh"angigen Schr"odinger-Gl. WW: E-Feld der Strahlung und E-Feld der Eigenfunktion - Symmetrien sind wichtig - "Ubergangsdipolmoment \underline{grob:} Auswahlregeln ("Ubergang erlaubt oder verboten) !! vorne noch dazuschreiben:
   • Mikrowellen = Rotationen} der Gesamtmolek"ule einfachstes Modell: starrer Rotator H: $E_{kin.}$ von Rotation E-Lsg.: $E=BJ(J+1)$ mit $B=\frac{h}{8 \pi^2 I c}$ und $I=\mu r_0^2$ Auswahlregel: $\Delta J = \pm 1$ (2,6,12,20,..) Spektrum: alle 2B eine Linie (2,4,6,...)
   • IR/Raman = interne Schwingungen} Modell: harmonischer Oszillator H: $E_{kin.}$ + $E_{Hook}$ E-Lsg: $E_v=h \nu (v+\frac{1}{2})$ Auswahlregel: $\Delta v= \pm 1$ Spektrum: eine Linie, da alle E "aquidistant
   • UV/VIS = $e^-$-"Uberg"ange} in Atomen/Molek"ulen Modell I: H-Atom: H: $E_{kin.}$ + $E_{pot.}$ von $e^-$ am Proton E-Lsg: $E_n = - \frac{R}{n^2}$ (mit R=Rydbergkonstante 13.6 eV) Auswahlregel: $\Delta$ n beliebig Spektrum: $\mapsto$ bekanntes Spektrum (Balmer-, Lyman- usw. Serie)
3. weitere Einfl"usse bzw. Abweichungen hiervon durch div. Relaxationsprozesse
   • Lichtstreuung in L"osungen
   • Reflexion an K"uvettenw"anden
   • Fluoreszenz
   • Molek"uldissoziation
   • ...

Linienbreiten

• Die Sto"sverbreitung h"angt im wesentlichen vom Aggregatzustand der Probe ab. Teilchen sto"sen miteinander und werden dabei deformiert. Die Sto"sverbreiterung ist bei fl"ussigen Proben daher deutlich gr"o"ser als bei Gasen, bei Festk"orpern ist sie nur sehr klein. Die Sto"sverbreitung ist Linienbreiten-bestimmend bei der Spektroskopie von Molek"ulbewegungen (IR, RAMAN, Mikrowellen) und der Anregung "au"serer Elektronen (UV/VIS).
• Die Dopplerverbreiterung resultiert aus dem Dopplereffekt (Bewegung der Teilchen realiv zur Ausbreitungsrichtung der Strahlung) und ist daher bei bei Gasen gr"o"ser als bei Fl"ussigkeiten. Bei Gasen ist sie meist der Hauptfaktor f"ur die Linienverbreiterung.

• Heisenberg'sche Unsch"arfe (Physik, nicht "anderbar) PC-III: !! bei nichtkommutative Operatoren treten bei Messungen der einen !! Observablen St"orungen durch die andere Observable auf !! Energie E und (Relaxations)zeit sind so ein Paar E-Unsicherheit $\delta$ E f"ur die Dauer der Anregung $\tau$ \fbox{$\delta E \tau \approx \hbar$} mit $\delta E$: Energieunsch"arfe $\tau$: Lebensdauer des anger. Zustands (Relaxationszeit) $\tau$ gering beim gro"sem $\Delta$E (System will schnell in Grundzustand) $\mapsto$ bei hochenergetischen SP $\mapsto$ wegen Unsch"arfe $\mapsto$ $\delta$E gro"s $\mapsto$ schlechte E-Aufl"osung = gro"se Linienbreite

Zeiten

1. Wie Zeit, die die Strahlung mit den Teilchen in Wechselwirkung tritt betr"agt in der Hertz-Skala 10^{-16} bis 10^{-19} s, ist also schneller als alle anderen Prozesse Die Konsequenz davon ist, da"s jedes Photon einen anderen Zustand (bgzl. Schwingung, elektrischer Anregung usw.) sieht!
2. Die Relaxationszeit \tau ist die Lebenszeit des angeregten Zustands (s.o.). Obwohl keine einfache allgemeing"ultige Beziehung zwischen der Relaxationszeit und dem Energieunterschied des Grund- und des angeregten Zustands $\Delta$ E besteht, aber im Allgemeinen + verst"andlich (vgl. Pfeile in E-Schema) $\mapsto$ je gr"o"ser $\Delta$ E umso kleiner ist $\tau$ (System will wieder schnell in Grundzustand) (alle Pfeile auf E-Vorlage zeigen in eine Richtung) von 10 s (bei NMR) bis $10^{-15}$ s ($e^-$-Anregung)

   Beispiele: {\bf NMR:} $\Delta$E klein $\mapsto$ $\tau$ gro"s (bis 10 s) $\mapsto$ $\delta$E klein ($10^{-1}$ Hz) (wegen Unsch"arfe-Relation) $\mapsto$ sehr geringe Linienbreiten {\bf UV/VIS:} $\Delta$E gro"s $\mapsto$ $\tau$ klein (ca. $10^{-15}$ s) $\mapsto$ $\delta$E gro"s ($10^{15}$ Hz) $\mapsto$ sehr gro"se Linienbreiten (verdecken oft alle Feinstruktur)

3. Die Aufl"osungszeit ist f"ur die Untersuchung dynamischer (molekularen oder chemischen) Prozessen (wie z.B. der sog. Berry-Rotation von PF5: $10^2$ Hz) wichtig. Diese zeitliche Aufl"osung wird durch die Linienbreite/Abst"ande in der Frequenzskala bestimmt, d.h. Linienbreiten $\delta$E m"ussen zur Bestimmung der Aufl"osungszeit lediglich in die Frequenzskala umgerechnet werden.

   Beispiele: {\bf NMR:} $\mapsto$ kleines $\delta$E $\mapsto$ kleines $\nu$ $\mapsto$ langsame Methode $\mapsto$ z.B. f"ur F-NMR im Beispiel oben: zwei F mit 100 Hz Abstand im Spektrum bei Austausch mit $>$ 100 Hz $\mapsto$ eine Linie (beide Zust"ande in der t-Skala der Methode "aquivalent) Rkt. "ahnlich schnell wie Linienabstand $\mapsto$ breite Linie langsamerer Austausch $\mapsto$ Aufl"osung 2er F-Spezies \psfig{figure=./Xfig_bilder/t_aufloesung.eps,width=8.0cm,angle=0.} {\bf IR:} $\mapsto$ normale Aufl.: $1 cm^{-1}$ = $10^{10}$ Hz (sehr schnell) $\mapsto$ gute Aufl"osung: ca. $10^{-4}$ $cm^{-1}$ = $10^6$ Hz $\mapsto$ nur Prozesse schneller $10^{10}$ bzw. $10^6$ Hz untersuchbar $\mapsto$ alles langsamere = 2 Signale Frequenzskala der Linienbreiten $\mapsto$ dynamische chem. Prozesse i.A. nur mit NMR aufl"osbar (langsame Methode) $\mapsto$ alle anderen SP-Arten sehen beide Zust"ande einzeln (d.h. zu schnell)

4. Die Gesamtmesszeit ergibt sich bei der Mittelung "uber alle Prozesse. Sie h"angt prim"ar auch von der Aufnahmetechnik ab: Bei CW-Experimenten wird nur jeweils nue eine Energie/Wellenl"ange gemessen, so da"s entsprechende Messungen/Ger"ate entsprechend langsam sind. Die meisten spektroskopischen Methoden weren heute in der (F)FT-Technik (Fast-Fourier-Transform) betrieben, bei der alle Energien zusammen registriert werden und mit Interferometern und die entsprechend schnell sind.

<<<

Inhalt

Einleitung

I. Spektroskopie

II. Beugung

III. Bildgebung

IV. Sonstige Methoden

>>>

cr_home

Metalle

Nichtmetalle

FK-Chemie

Strukturchemie

Interm. Phasen

Oxide

Silicate

Strukturtypen

AFP