Symmetrie: Anwendungen in der Chemie

2.5.1. Moleküle

Beispiele für Moleküle und Kristallpolyeder

geordnet nach Punktgruppen gemäß Schönflies-Nomenklatur

Im Folgenden sind für alle 32 kristallographischen und einige nichtkristallographische Punktgruppen Beispiele (Moleküle und Kristallpolyeder) gezeigt. Die Gruppierung der Beispiele folgt der Schönflies-Nomenklatur. Zur entsprechenden Benennung nach Hermann-Mauguin sind die stereographischen Projektionen (mit einem Punkt allgemeiner Lage) und die einzelnen Bezeichnungsrichtungen angegeben. Die Farbkodierung der Symmetrieelemente und Bezeichnungsrichtungen in den nicht kubischen Punktgruppen ist:

rot 1. Richtung (z)
blau 2. Richtung (x)
grün 3. Richtung (d)

Zu einigen Punktgruppen gibt es auch VRMLs der Moleküle/Polyeder mit und ohne eingezeichnete Symmetrieelemente. Hier gilt ebenfalls die oben angegebene Farbkodierung.

Reine Drehgruppen C_n

Die Gruppen C_n weisen nur n-zählige Drehachsen als einziges Symmetrielement auf. Die Beispiele sind damit von der Vorlage 2.1. bekannt. Bei Molekülen sind diese sogenannten zyklische Gruppen (daher das C) selten. Die Ordnung entspricht der Zähligkeit n der Drehachse. Die Hauptachse ist polar, die Objekte sind chiral (s.u, z.B. Propeller), weil Symmetrieelemente 2. Art fehlen. Die Hermann-Mauguin-Bezeichnung ist n (n=1,2,3,4,6), es gibt nur eine Richtung (Hauptachse) in der die Drehachse liegt.

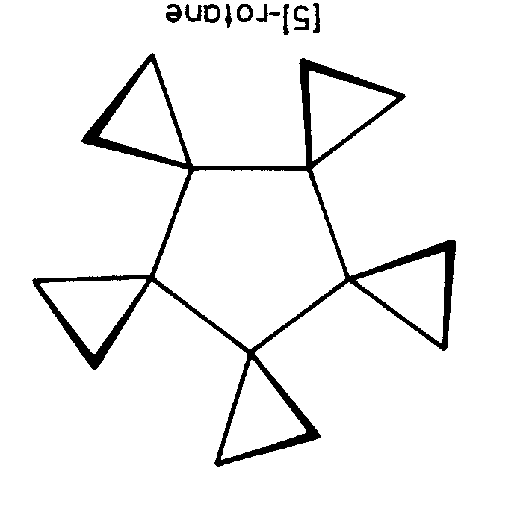
Schönflies H.M. stereographische Projektion Molekül Kristall

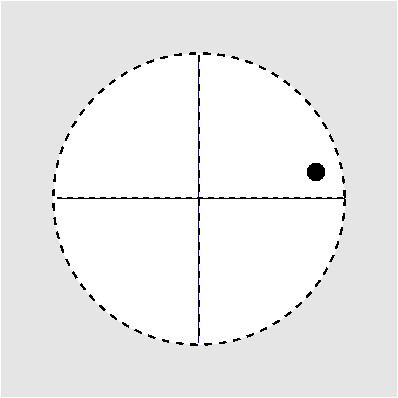
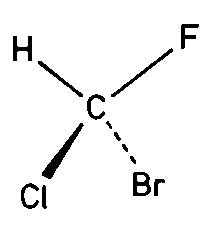
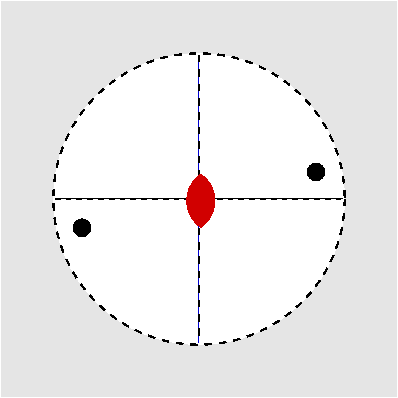
C₁ 1

SrH₂(C₄H₄O₆)₂ 4 H₂O

C₂ 2

C₁₂H₂₂O₁₁

C₃ 3

NaIO₄ 3 H₂O

C₄ 4

Ba(SbO)₂(C₄H₄O₆)

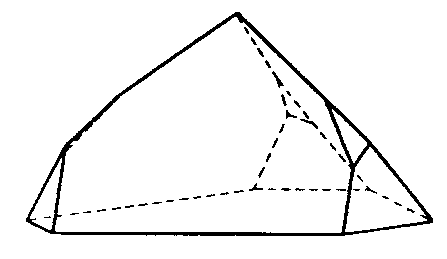
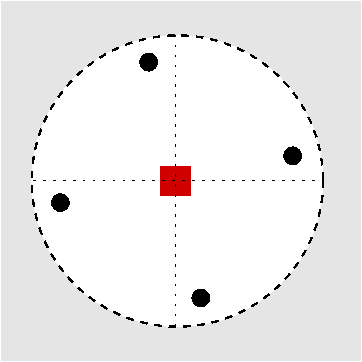
C₅ - -

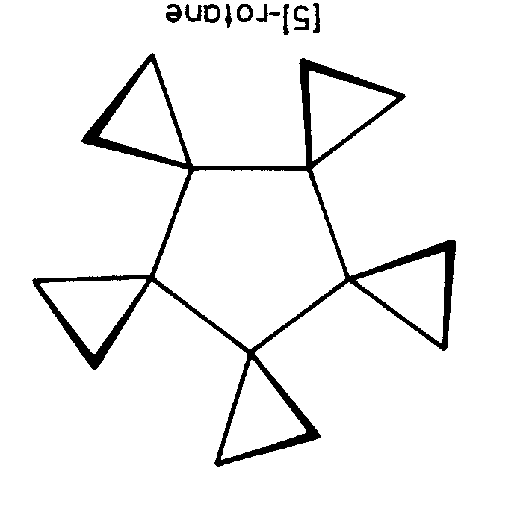(5)-Rotane

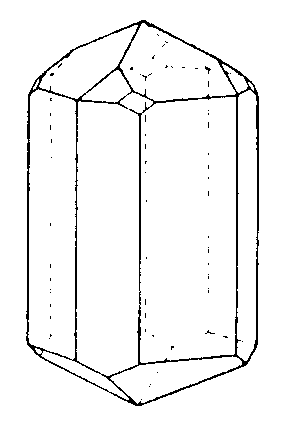
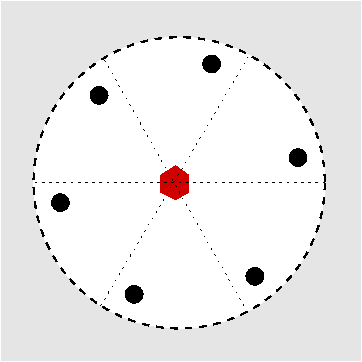
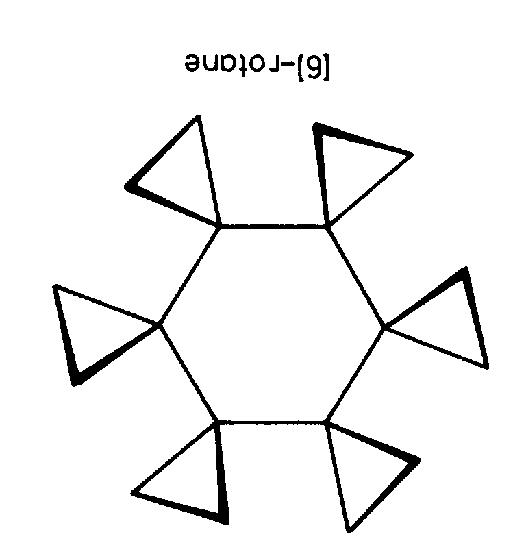
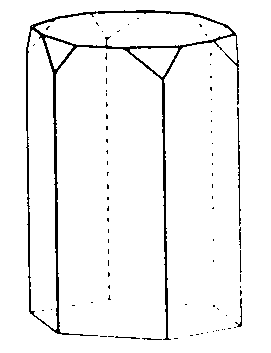
C₆ 6

(6)-Rotane NaK₃Al₄Si₄O₁₆

C_s: Spiegelebene alleine

Objekte mit der Punktgruppe C_s haben eine Spiegelebene (m) als einziges Symmetrieelement. Beispiele s. Vorlage 2.2. Die Objekte sind nicht chiral, die Ordnung der Gruppe ist 2. Sowohl bei Molekülen als auch bei Kristallen ist die Punktgruppe C_s recht häufig. Die Hermann-Mauguin-Bezeichnung ist m, entsprechend -2 (2-quer d.h. eine zweizählige Drehinversionsachse).

Schönflies	H.M.	stereographische Projektion	Molekül	Kristall
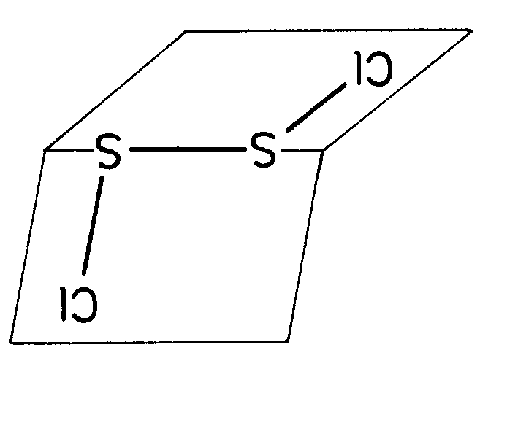
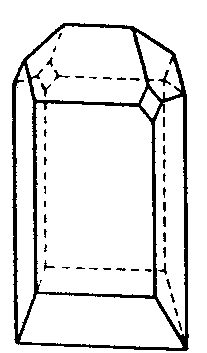
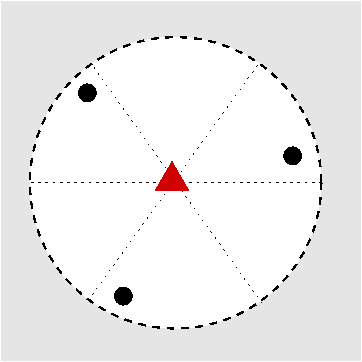
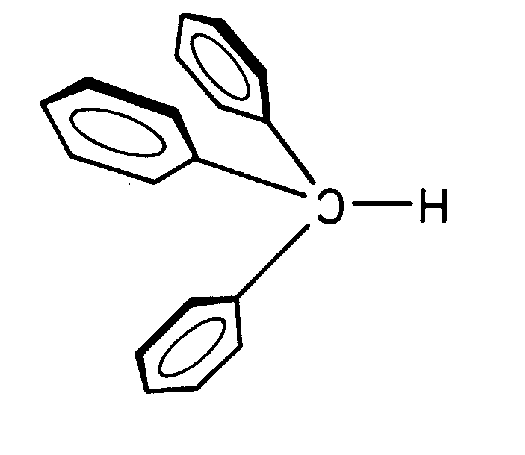
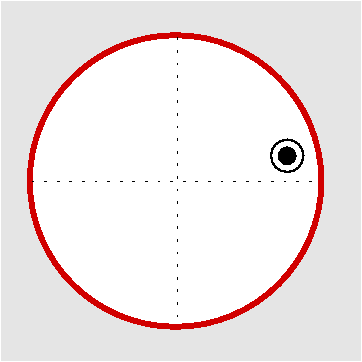
C_s	m
				Ca₈B₁₈O₃₃Cl₄ 4 H₂O

C_i: Inversionszentrum alleine

Die Punktgruppe C_i hat die Inversion (i) ist einziges Symmetrieelement und einzige Symmetrieoperation. Beispiele sind ebenfalls auf der Vorlage 2.2 zu finden. Wie Objekte mit Punktgruppe C_s sind auch die mit C_i nicht chiral. Die Hermann-Mauguin-Bezeichnung ist -1 (eins-quer).

Schönflies	H.M.	stereographische Projektion	Molekül	Kristall
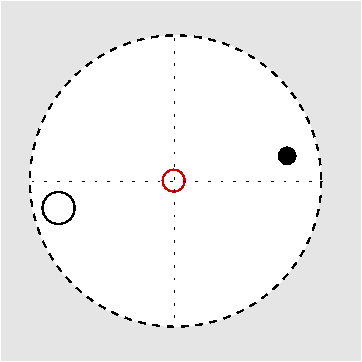
C_i	-1
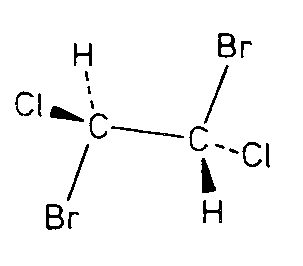				MnSiO₃

C_nv: Drehachsen mit vertikalen Spiegelebenen

Objekte mit Punktgruppen C_nv haben neben der n-zähligen Drehachse noch n vertikalen Spiegelebenen (vgl. Vorlage 2.6.). Die Gruppenordnung ist 2n. Moleküle und Kristalle mit diesen Punktgruppen sind sehr weit verbreitet, wichtig z.B. das Wassermolekül mit C_2v- oder Ammoniak mit C_3v-Symmetrie. Die Punktgruppen C_5v und C_∞v (d.h. linear ohne vertikale Spiegelebene) sowie die mit allen anderen Drehachsen sind nichtkristallographisch, d.h. nicht mit der Translationssymmetrie vereinbar. Für gerade n ist die Hermann-Mauguin-Bezeichnung nmm, für ungerade n (n=3) nur nm, da z.B. für n=3 keine Spiegelebene senkrecht zur Diagonalen (3.Richtung) liegt.

Schönflies	H.M.	stereographische Projektion	Molekül	Kristall
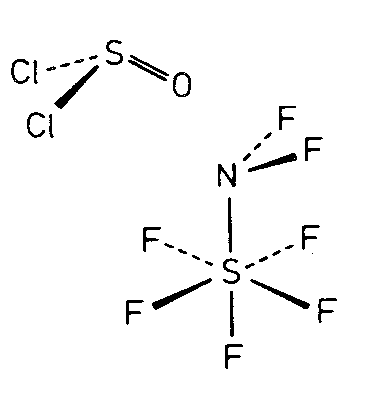
C_2v	2 mm	SVG
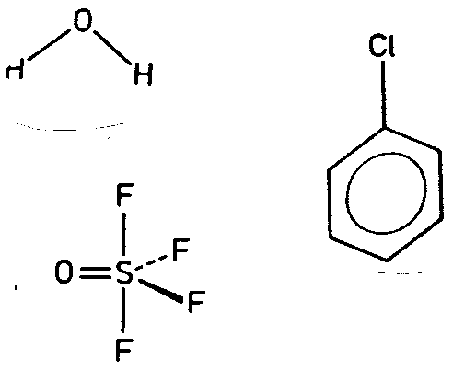				Mg(NH₄)PO₄ 6 H₂O
			H₂O (2mm): Molekül alleine und mit SE
			SO₂Cl₂ (2mm) Molekül alleine und mit SE
C_3v	3 m	SVG
				Turmalin
C_4v	4 m m	SVG
				AuS(CH₂C₆H₅)₂Cl
C_5v	-
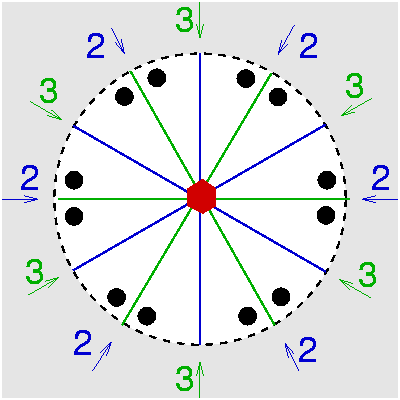
C_6v	6 m m	SVG
				Bromellit (BeO)

C_nh: Drehachsen mit horizonaler Spiegelebene

Die Gruppen C_nh haben neben der n-zähligen Drehachse noch zusätzlich eine horizontale Spiegelebene. (s. Vorlage 2.7.). Diese wird in der stereographischen Projektion durch die ausgezogene Linie in der Projektionsebene angegeben. Durch diese Spiegelebene kommen alle Punkte sowohl über- als auch unter der Papierebene zu liegen, die Gruppenordnung ist damit 2n. Wegen der Spiegelebene sind Objekte mit diesen Punktguppen zentrosymmetrisch. Bei Molekülen sind diese Gruppen, wie die untenstehenden Beispiele zeigen, recht selten. Die zugehörige Hermann-Mauguin-Bezeichnung ist n/m, wobei allerdings für 3/m meist -6 genannt wird.

Schönflies	H.M.	stereographische Projektion	Molekül	Kristall
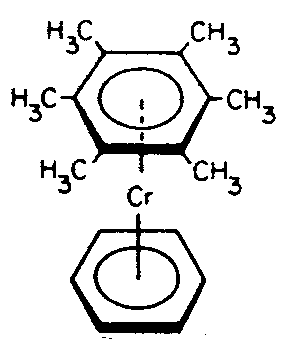
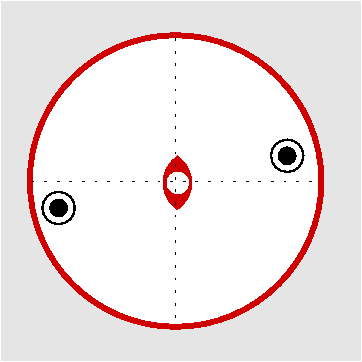
C_2h	2/m	SVG
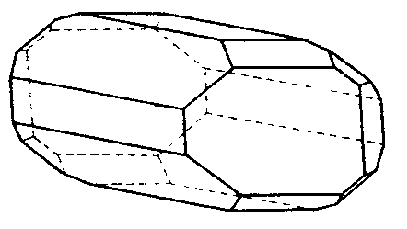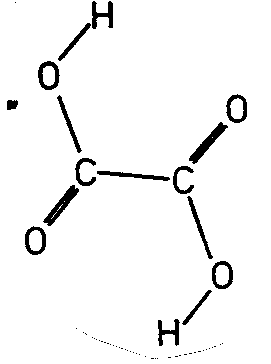
				BaS₂O₆ 2 H₂O
			Oxalsäure C₂O₄H₂: (2/m) Molekül alleine und mit SE
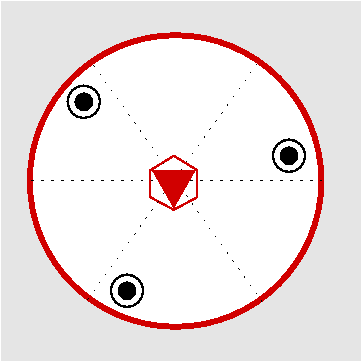
C_3h	3/m= -6	SVG
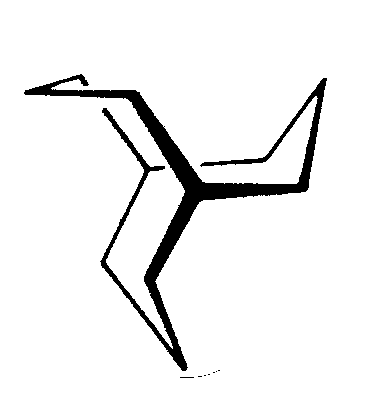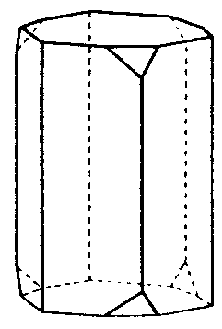				Li₂O₂
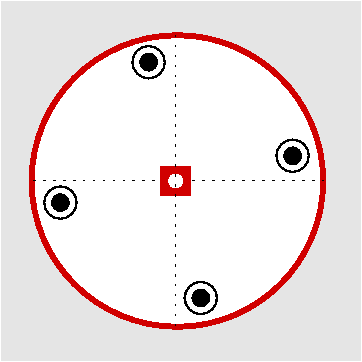
C_4h	4/m	SVG
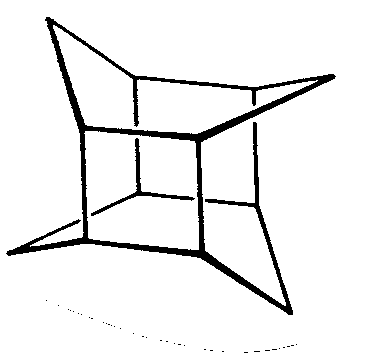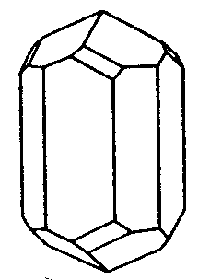				Na₄Al₃Si₉O₂₄Cl (Meionit)
C_6h	6/m	SVG
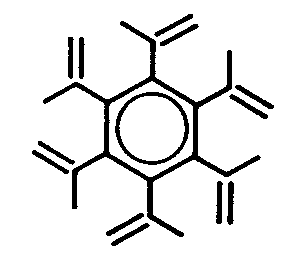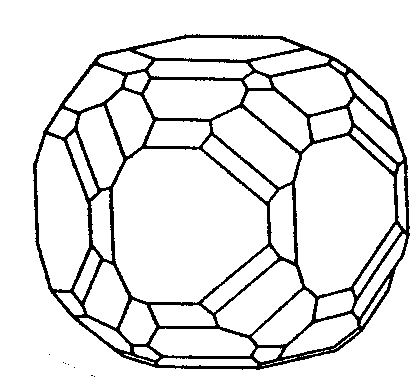				Ca₅(PO₄)₃F (Apatit)

D_n: n-zählige Drehachse mit senkrechten 2-zähligen Achsen

Die Diedergruppen D_n weisen außer der n-zähligen Drehachse weitere 2-zählige Drehachsen auf, die senkrecht zu dieser Hauptachse liegen. Diese 2-zähligen Achsen kommen wegen der Hauptdrehachse n-mal vor (vgl. Vorlage 2.8.). Auf den Diagonalen (d, 3. Bezeichnungsrichtung für das Hermann-Mauguin-Symbol) entstehen noch weitere 2-zählige Achsen. Objekte mit D₂-Gruppen haben kein Inversionszentrum und keine Spiegelebene, d.h. sie sind chiral. Ein sehr wichtiges Beispiel aus dem Bereich der Kristallpolyeder ist der Quarz (PG D₃), von dem zwei 'Enantiomere' gefunden werden können. Bei Molekülen sind Beispiele mit D_n-Gruppen nicht sehr häufig. Ein Beispiel für D₂ ist Twistan. Das für die anorganische Chemie sehr wichtige Beispiel sind tris-chelat-Komplexe, die zur Punktgruppe D₃ gehören. Die Hermann-Mauguin-Bezeichnungen sind n2 (für ungerade n) bzw. n22 für gerade n.

Schönflies	H.M.	stereographische Projektion	Molekül	Kristall
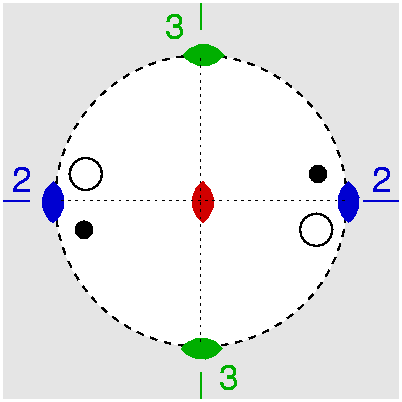
D₂	2 2 2	SVG
				Ba(HCOO)₂
			Twistan (222) Molekül mit SE
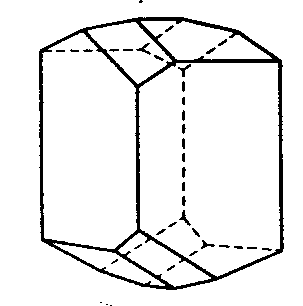
D₃	3 2	SVG
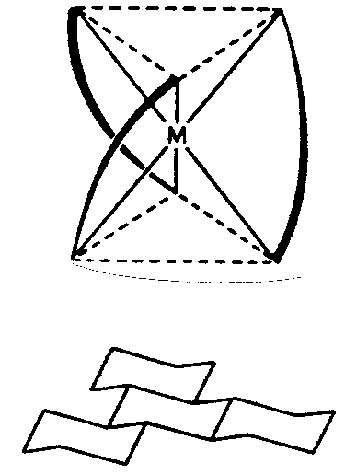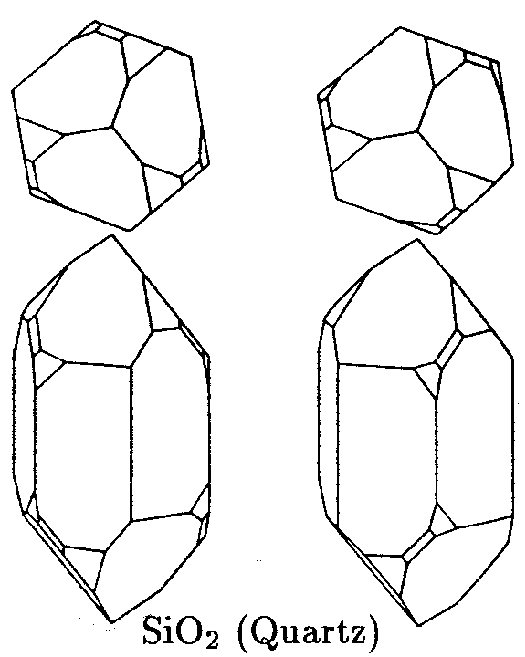			Tris-chelat-Komplexe (32) Molekül
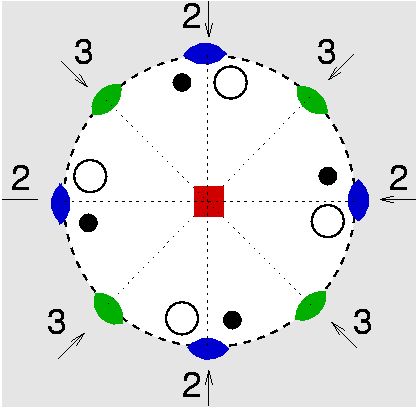
D₄	4 2 2	SVG
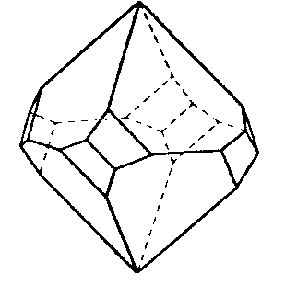				Cl₃CCO₂K . Cl₃CCO₂H
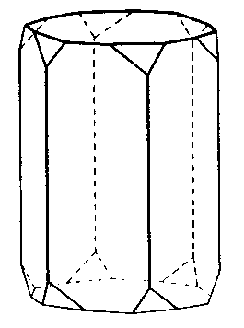
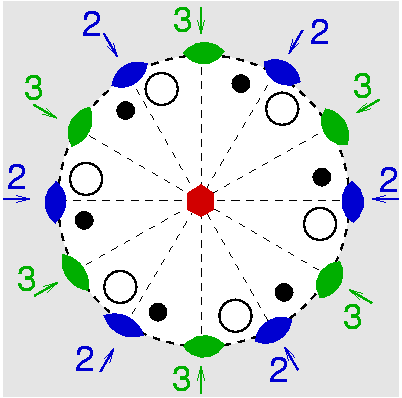
D₆	6 2 2	SVG
				SiO₂ (Quarz)

D_nh: D_n mit horizontaler Spiegelebene

Bei den Punktgruppen D_nh kommt zusätzlich zu D_n noch eine horizontale Spiegelebene hinzu. Die stereographischen Projektionen entsprechen damit denen von D_n, mit dem Unterschied, daß jeder Punkt allgemeiner Lage sowohl oberhalb als auch unterhalb der Zeichenebene vorkommt. Durch diese Symmetrien entstehen auch vertikale Spiegelebenen, wie sie z.B. bei den Gruppen C_nv vorliegen (vgl. Vorlage 2.9.) Die Hermann-Mauguin-Bezeichnung für ungerade n ist -n 2/m, für gerade n lautet sie n/m 2/m 2/m oder kurz n/mmm.

Schönflies	H.M.	stereographische Projektion	Molekül	Kristall
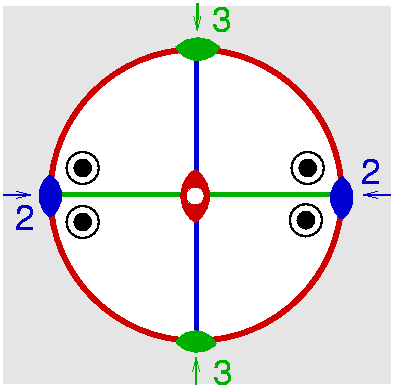
D_2h	m m m	SVG
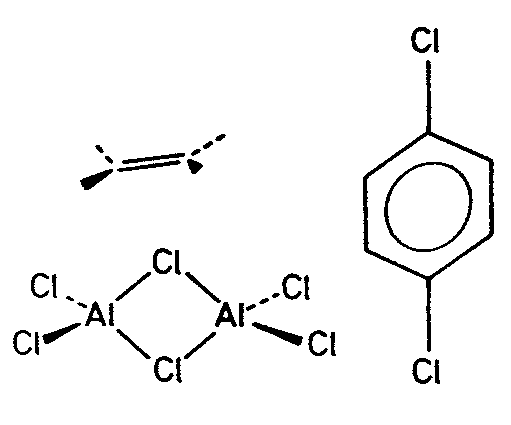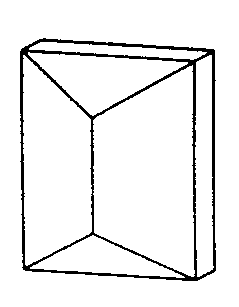				HFeAl₅Si₂O₁₃ (Staurolit)
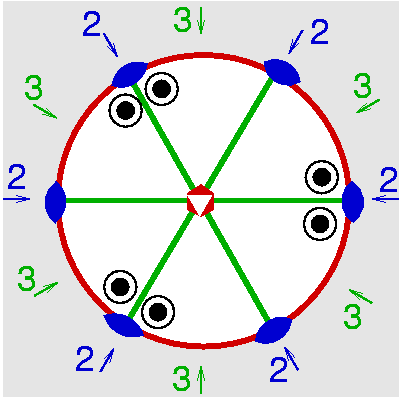
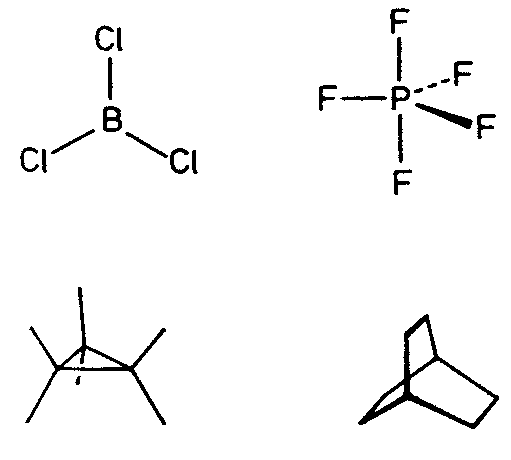
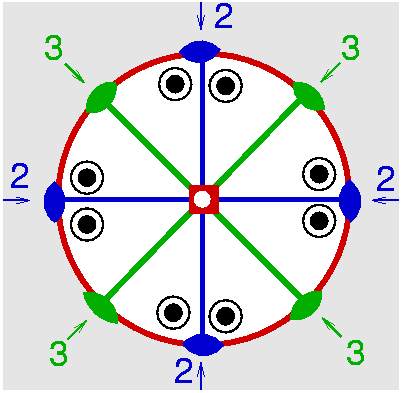
D_3h	-6 2 m	SVG
				BaTiSi₃O₉
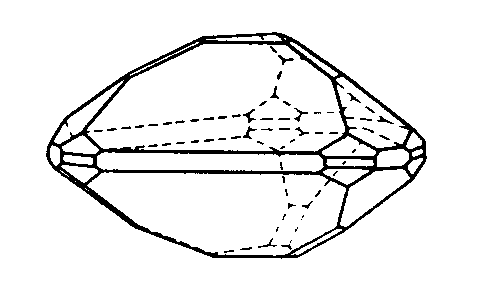
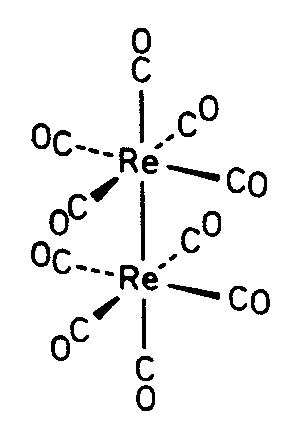
D_4h	4/mmm = 4/m2/m2/m	SVG
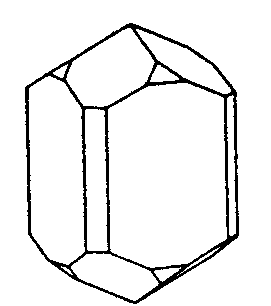				TiO₂ (Rutil)
			Re₂(CO)₁₀: Molekül alleine, mit 4/m in z, mit 2/m in x, mit 2/m in d und mit allen SE	Rutil: Kristall alleine, mit 4/m in z, mit 2/m in x, mit 2/m in d und mit allen SE
D_5h	-
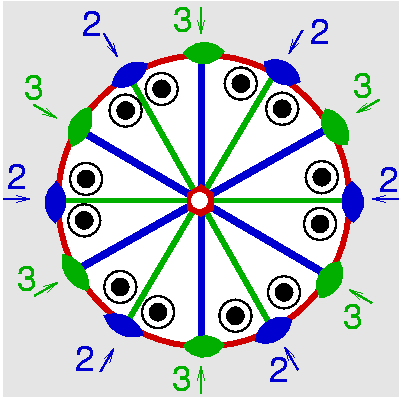
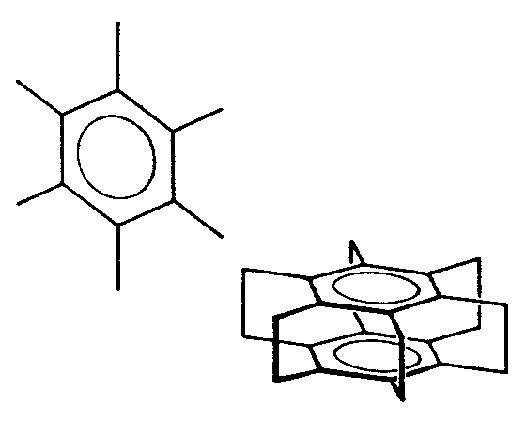
D_6h	6/m 2/m 2/m	SVG
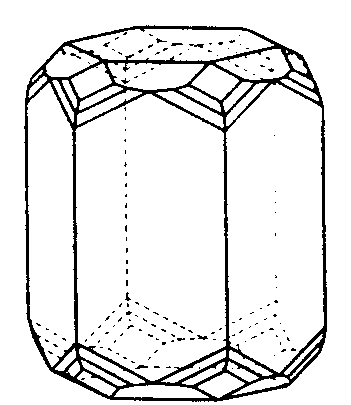				Be₃Al₂Si₆O₁₈ (Beryll)
D_∞h	-		O=C=O, H-H

D_nd: D_n mit diagonalen Spiegelebenen

Objekte mit den Punktgruppen D_nd (vgl. Vorlage 2.10.) haben neben der n-zählige Drehachse noch n horizontale 2-zählige Achsen winkelhalbierend (diagonal). Dadurch entstehen auch 2n-zählige Drehspiegelachsen, und n vertikalen Spiegelebenen. Die Hermann-Mauguin-Bezeichnungen s.u.

Schönflies	H.M.	stereographische Projektion	Molekül	Kristall
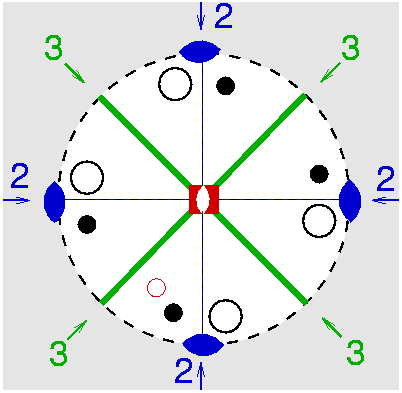
D_2d	-4 2 m	SVG
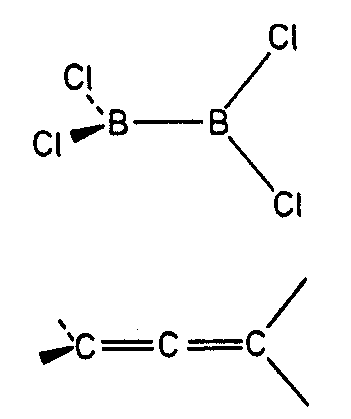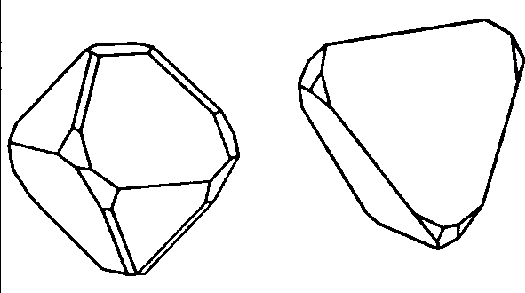				CuFeS₂ (Chalkopyrit)
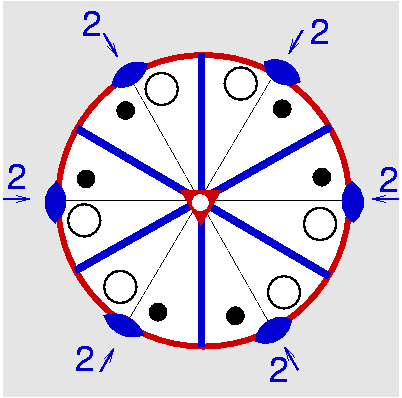
D_3d	-3 m = -3 2/m	SVG
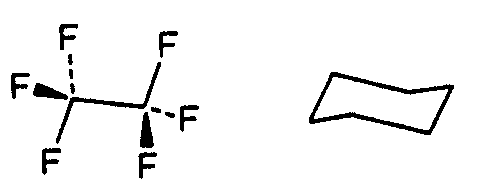				CaCO₃ (Calcit)
D_4d	-
			Mn₂(CO)₁₀: Molekül alleine, mit 4/m in z, mit 2/m in x, mit 2/m in d und mit allen SE
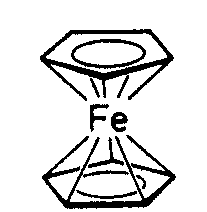
D_5d	-

S_n: Drehspiegelebenen alleine

Gruppen mit Drehspiegelachsen (Schönflies) bzw. Drehinversionsachsen (Hermann-Mauguin) alleine werden mit S_n bzw. -n bezeichnet (vgl. Vorlage 2.10.) Es liegt nur eine n-zählige Drehspiegel- bzw. Drehinversionsachse vor. ACHTUNG, die n sind zwischen Hermann-Mauguin- und Schönflies meist verschieden!! Auch diese Gruppen wurden bereits bei der Einführung der 'zusammengesetzten' Symmetrieoperationen genannt. Hier noch Molekülbeispiele:

Schönflies	H.M.	stereographische Projektion	Molekül	Kristall
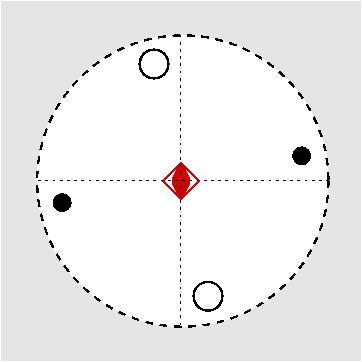
S₄	-4	SVG
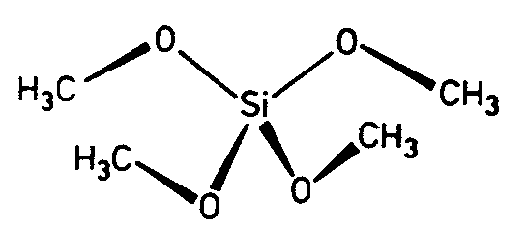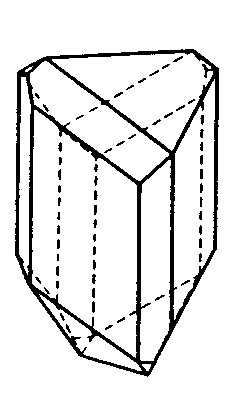				CaB(OH)₄AsO₄ (Cahnit)
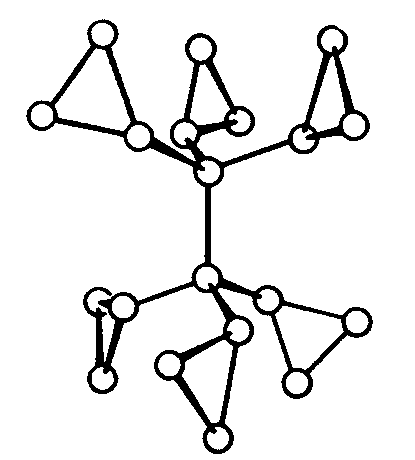
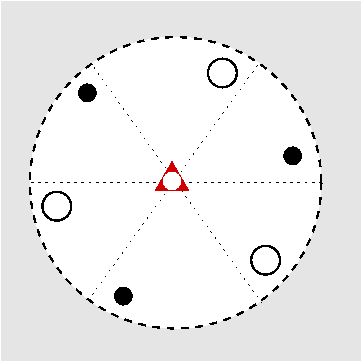
S₆	-3	SVG
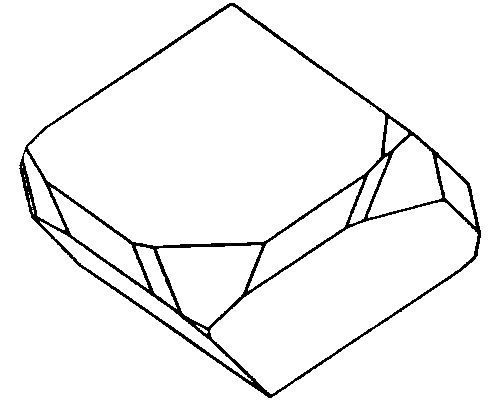				CaMg(CO₃)₂

Tetraeder- und Oktaeder-Punktgruppen

Die Tetraeder- und Oktaedergruppen (Vorlage 2.11.) haben gemeinsam:

vier 3-zählige Achsen, die untereinander Winkel von 109.47 ^o einschließen, d.h. die beispielsweise die Raumdiagonalen eines Würfels (x+y+z, x-y+z, -x+y+z, x+y-z) bilden.
in Richtung x=y=z liegen Achsen 4, -4 oder 2, senkrecht dazu können Spiegelebenen vorhanden sein.

Für die Benennung gilt:

H.M.:
- 1. Richtung: x,y,z (also die Würfelkanten) (rot)
- 2. Richtung: die vier Raumdiagonalen (also immer 3 an 2. Position des Symbols!) (blau)
- 3. Richtung: x+y, ... usw. (alle Flächendiagonalen des Würfels) (grün)
Schönflies
- für jede Punktgruppe ist ein eigenes Symbol eingeführt.

Kurze Erklärungen zu den einzelnen kubischen Punktgruppen:

T: Objekte mit der Punktgruppe T = 23 haben die minimale Tetraedersymmetrie: vier dreizählige Achsen, zusätzlich 2-zählige Achsen in x, y und z (2. Blickrichtung). Es handelt sich damit um chirale Objekte, die Gruppenordnung ist 12. Bei Molekülen wie Pt(PF₃)₄ aus dem Beispiel unten bitte beachten, dass die PF₃-Gruppen etwas um die Raumdiagonalen gedreht werden müssen (also nicht genau staggered oder eclipsed stehen dürfen), damit die diagonale Spiegelebene entfällt.
T_h: Zusätzlich zu den für T genannten Symmetrieelementen kommen Spiegelebenen senkrecht zu den 2-zähligen Achsen hinzu. Durch diese Kombination von Symmetrieelementen sind die dreizähligen Achsen zugleich auch Drehinversionsachsen (-3). Damit ergibt sich für die Benennung nach Hermann-Mauguin m -3 als Kurz- und 2/m -3 als Langsymbol. Die Gruppenordnung ist 24. Die Punktgruppe ist auch als Oktaeder anzusehen, dem die vierzähligen Achsen fehlen.
T_d: bedeutet volle Tetraedersymmetrie. Die Gruppenordnung ist 24. Zusätzlich zu T liegen diagonale Spiegelebenen vor, d.h. das Hermann-Mauguin-Symbol ist -4 3 m.
O: Die Oktaedergruppen unterscheiden sich von den Tetraedergruppen durch die 2-zähligen Achsen auf den Diagonalen. O ist eine Punktgruppe ohne alle Spiegelebenen, d.h. 4 dreizählige, 6 vierzählige und 12 zweizählige Achsen. Die Gruppenordnung ist 24. Die Objekte sind chiral, die Kristalle aber ohne piezoelektrische Eigenschaften.
O_h: beschreibt Oktaeder bzw. Würfelsymmetrie (Oktaeder und Würfel gehören damit zur selben Punktgruppe. Sie sind zueinander dual, wenn Flächen durch Ecken ersetzt werden sind die beiden Polyeder ineinander überführbar. Die Gruppenordnung ist 48 (d.h. ein Punkt allgemeiner Lage kommt 48 mal vor, daher fehlen diese Punkte auf den folgenden Zeichnungen).

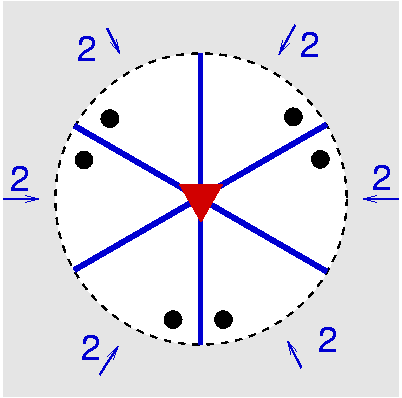
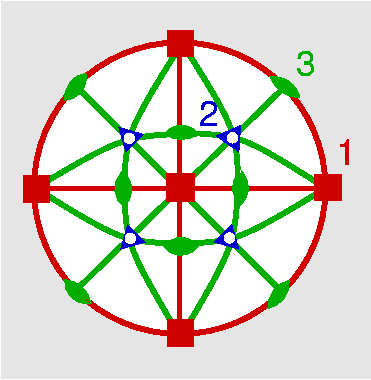
Prinzip der stereographischen Projektion:

SVG-Datei dazu

Schönflies H.M. stereographische Projektion Molekül Kristall

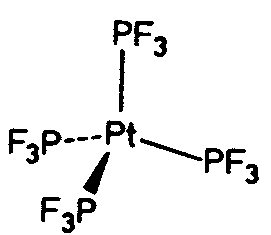
T 23
SVG

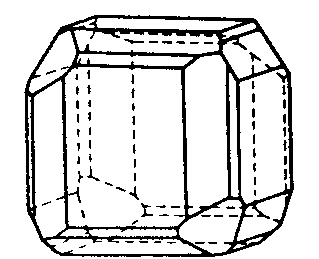NaClO₃

T_h 2/m -3 = m -3
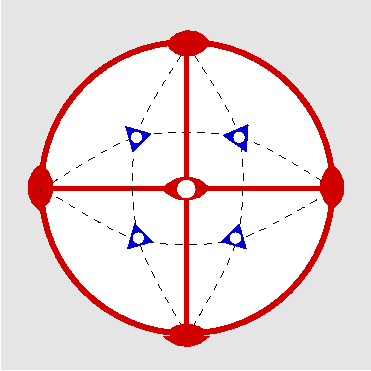
SVG

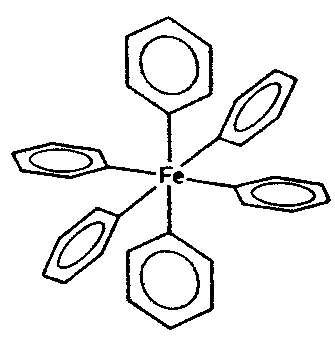FeS₂ (Pyrit)

T_d -4 3 m
SVG

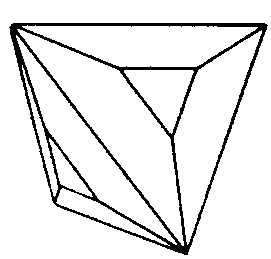ZnS (Sphalerit)

O 432
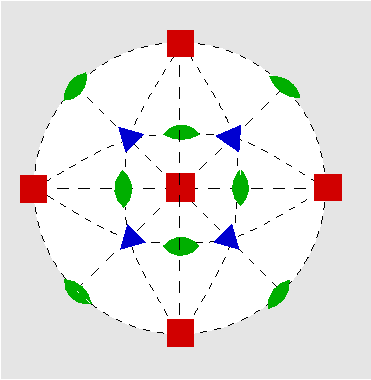
SVG

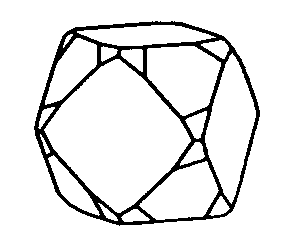Cu₂O

O_h 4/m -3 2/m = m -3 m = m 3 m
SVG

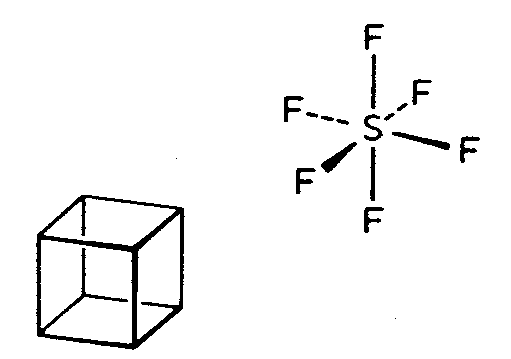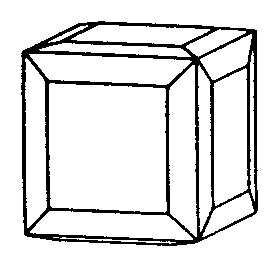Cu

Im folgenden wegen der großen Zahl an Symmetrieelementen und der Bedeutung von Tetraedern und Oktaedern in der Chemie einige VRMLs:

T_d-Symmetrie
- Symmetrielemente alleine, entlang der
  - Achsen: x, y, z (1. Richtung): 3 Drehinversionsachsen -4
  - Raumdiagonalen: x+y+z usw. (2. Richtung): 4 3-zählige Achsen
  - Flächendiagonalen: x+y(3. Richtung): 6 Spiegelebenen
- Tetraeder alleine
- Tetraeder mit Symmetrieelementen entlang der
  - Achsen: x, y, z (1. Richtung): 3 Drehinversionsachsen -4
  - Raumdiagonalen: x+y+z usw. (2. Richtung): 4 3-zählige Achsen
  - Flächendiagonalen: x+y(3. Richtung): 6 Spiegelebenen
O_h-Symmetrie
- Symmetrielemente alleine, entlang der
  - Achsen: x, y, z (1. Richtung): 3 * 4/m
  - Raumdiagonalen: x+y+z usw. (2. Richtung): 4 Drehinversionsachsen -3
  - Flächendiagonalen: x+y(3. Richtung): 6* 2/m
- 1. Beispiel: Oktaeder alleine
- Oktaeder mit Symmetrieelementen entlang der
  - Achsen: x, y, z (1. Richtung): 3 * 4/m
  - Raumdiagonalen: x+y+z usw. (2. Richtung): 4 Drehinversionsachsen -3
  - Flächendiagonalen: x+y(3. Richtung): 6 * 2/m
- 2. Beispiel: Würfel alleine
- Würfel mit Symmetrieelementen entlang der
  - Achsen: x, y, z (1. Richtung): 3 * 4/m
  - Raumdiagonalen: x+y+z usw. (2. Richtung): 4 Drehinversionsachsen -3
  - Flächendiagonalen: x+y(3. Richtung): 6 * 2/m

Gruppe-Untergruppe-Beziehung bei Dominosteinen

mit C_2v = 2mm-Symmetrie
mit C_4v = 4mm-Symmetrie
mit D_4h = 4/mmm = 4/m2/m2/m-Symmetrie
mit O_h = m3m = 4/m -3 2/m -Symmetrie
- Achsen: x, y, z (1. Richtung): 3 * 4/m
- Raumdiagonalen: x+y+z usw. (2. Richtung): 4 Drehinversionsachsen -3
- Flächendiagonalen: x+y (3. Richtung): 6 * 2/m

Gruppe-Untergruppe-Beziehung bei oktaedrischen Komplexen

anhand der 'alten' Beispiele aus der Vorlesung Chemie der Metalle zu möglichen Stereoisomeren bei oktaedrischen Komplexen.
(A,B und C stehen für unterschiedliche Liganden, A1 und A2 usw. sind jeweils Stereoisomere zueinander, vereinfachte Darstellung: jede gelbe Bindung steht für einen Chelatliganden!)

Zähnigkeit	Summenformel	Isomer A1	Isomer A2	Isomer B1	Isomer B2	Isomer C

einzähnig	MA₆	MA₆ (O_h,m3m)
	MA₅B	MA₅B(C_4v,4mm)
	MA₄B₂	cis(C_2v,2mm)		trans(D_4h,4/mmm)
	MA₃B₃	fac(C_3v,3m1)		mer(C_2v,2mm)
	MA₂B₂C₂	cis/cis/cis(C₁,1)	cis/cis/cis(C₁,1)	cis/cis/trans(C_2v,2mm)		trans/trans/trans(D_2h,mmm)

zweizähnig	M(AA)₃	A1 (D₃,32)	A2 (D₃,32)
ein- und zweizähnig	M(AA)₂B₂	A1 (C₂,2)	A2 (C₂,2)	B (D_2h,mmm)

ein- und vierzähnig	M(AAAA)B₂	A1(C₂,2)	A2(C₂,2)	B1(C₁,1)	B2(C₁,1)	C(C_2v,2mm)

Wichtige Punkte/Fragen bei diesen Beispielen:

Was ist die Voraussetzung für das Auftreten von Stereoisomeren?
Wie sieht der Gruppe-Untergruppe-Stammbaum für diese Beispiele aus?
Welche totalsymmetrischen Schwingungen (alle Liganden vom Metall-Zentrum weg) sind Raman-, welche IR-aktiv?

<<<<

Symmetrie: Anwendungen in der Chemie

2.5.1. Moleküle

Beispiele für Moleküle und Kristallpolyeder

geordnet nach Punktgruppen gemäß Schönflies-Nomenklatur

Reine Drehgruppen Cn

Cs: Spiegelebene alleine

Ci: Inversionszentrum alleine

Cnv: Drehachsen mit vertikalen Spiegelebenen

Cnh: Drehachsen mit horizonaler Spiegelebene

Dn: n-zählige Drehachse mit senkrechten 2-zähligen Achsen

Dnh: Dn mit horizontaler Spiegelebene

Dnd: Dn mit diagonalen Spiegelebenen

Sn: Drehspiegelebenen alleine