Vorlesung Chemie der Nichtmetalle
3. Edelgase
3.4. VSEPR-Modell (Gillespie-Nyholm-Konzeption)
|
Die sogenannte Gillespie-Nyholm-Konzeption auch VSEPR-Modell
= Valence shell electron pair repulsion oder VE-Abstoßungsmodell
erlaubt die Voraussage von Molekülgeometrien und Winkeln zwischen Atomen.
Ausgehend von einem Molekül AXn mit einer bestimmten Zahl n von Elektronenpaaren X,
die sich als Summe der Valenzelektronenpaare (L) und der freie Elektronenpaare (E) beschreiben läßt,
sind sämtliche Elektronenpaare so um das Zentralatom (A) angeordnet, dass
sie sich möglichst wenig untereinander beeinflussen, d.h. dass sie den größtmöglichen Abstand voneinander
einnehmen und die Winkel X-A-X maximal sind.
Grundgeometrien bei gleichen Liganden
 |
| Abb. 3.4.1. Grundgeometrien nach dem VSEPR-Konzept
‣SVG
|
Als Grundgeometrien ergeben sich für die unterschiedlichen n in Molekül AXn
- n=2: Zwei Liganden X/Elektonenpaare liegen immer diametral gegenüber, die Moleküle sind
linear, der Bindungswinkel X-A-X beträgt 180o.
- n=3: Drei Liganden X/Elektonenpaare ordnen sich in den Ecken eines Dreiecks an,
die Geometrie wird als trigonal planar beschrieben.
Der Bindungswinkel X-A-X beträgt 120o.
- n=4: Die ideale Geometrie bei vier Liganden X/Elektonenpaaren ist die
eines idealen Tetraeders; der Bindungswinkel beträgt 109.4o.
- n=5: Die Grundgeometrie bei fünf Liganden X/Elektonenpaaren ist die
trigonale Bipyramide. Die Bindungswinkel sind 120o zwischen
den drei äquatorialen und 90o zwischen den axialen und den
äquatorialen Liganden.
- n=6: Die Oktaeder-Anordnung ist der günstigste Fall bei
sechs Liganden X/Elektonenpaaren. Das Oktaeder läßt sich als
Spezialfall einer quadatischen Bipyramide (1:4:1-Anordnung von X) oder
als Sonderfalls des trigonalen Antiprismas (3:3-Anordnung) betrachten.
Die Bindungswinkel zwischen benachbarten Liganden sind 90o.
- n=7: Bei sieben Liganden X/Elektonenpaaren gibt es unterschiedliche
Grundpolyeder, die sich allerdings nur sehr wenig in ihren Energien unterscheiden:
- Das einfach überkappte Oktaeder (1:3:3).
- Die pentagonale Bipyramide (1:5:1)
- Eine als 1:2:2:2 zu beschreibende Anordnung.
- n=8: Auch bei acht Liganden X/Elektonenpaaren liegen die
beiden wichtigsten Grundgeometrien:
- archimedisches Antiprisma
- oder archimedisches Prisma (Würfel)
energetisch ebenfalls eng beieinander.
Geometrien bei unterschiedlichen Liganden
Bei unterschiedlichen Liganden gelten für die Möglichkeiten der Anordnung die folgenden Regeln:
- Freie Elektronenpaare beanspruchen den größten Raum, die Winkel zu anderen Liganden
sollten daher maximal sein.
- Doppelbindungen brauchen mehr Platz als Einfachbindungen.
- Die Liganden L brauchen nach der Elektronegativität abgestuften Platz, je großer
die Elektronegativität ist, umso stärker ist die Elektronendichte zum
Liganden verschoben, umso weniger Platz wird also am Zentrum benötigt.
Daraus folgt:
- Bei linear, trigonaler und tetraedrischer Geometrie ist die Liganden/Elektronenpaar-Verteilung
völlig egal (gleiche Winkel zwischen allen Liganden).
- Bei der trigalen Bipyramide (CN=5) liegen zwischen äquatorialer Liganden
120o, zwischen äquatorialen und terminalen jedoch nur 90o.
Die äquatoriale Position ist als günstiger für voluminöse
Bindungspartner wie z.B. freie Elektronenpaare. Diese besetzen demnach
bevorzugt äquatoriale Positionen.
| CN |
Bezeichnung (alle) |
Bezeichnung (nur L) |
VRML-Bild |
Beispiele |
| 2 |
linear |
linear |
ML2 |
BeCl2 |
|
| 3 |
trigonal |
trigonal |
ML3 |
BCl3 |
| gewinkelt (120o) |
ML2E |
SnCl2 |
|
| 4 |
tetraedrisch |
tetraedrisch |
ML4 |
CH4 |
| psi-tetraedrisch |
ML3E |
NH3 |
| gewinkelt (109 Grad) |
ML2E2 |
H2O |
| 5 |
trigonal bipyramidal |
trigonal bipyramidal |
ML5 |
PCl5 |
| psi-trigonal bipyramidal |
ML4E |
SF4 |
| T-förmig |
ML3E2 |
ClF3 |
| linear |
ML3E2 |
XeF2 |
| 6 |
oktaedrisch |
oktaedrisch |
ML6 |
SF6 |
| quadratisch-pyramidal |
ML5E |
BrF5 |
| quadratisch |
ML4E2 |
XeF4 |
| 7 |
verschiedene |
pentagonal-bipyramidal 1-5-1 |
ML7 |
IF7 |
| Grund- |
überkappt oktaedrisch 1-3-3 |
ML7 |
|
| geometrien |
1-2-2-2 |
ML7 |
|
|
| 8 |
quadratisch antiprismatisch |
quadratisch antiprismatisch |
ML8 (Polyeder),
(Stick+Ball) |
XeF82- |
|
|
| Tab. 3.4.1. VRML-Bilder der wichtigsten Koordinationsgeometrien
(L = echte Liganden; E = einsame Elektronenpaare (in den VRML-Bildern nur als Bindungsreste in gelb angedeutet)
|
Anwendung auf Edelgasverbindungen (Rechenbeispiele)
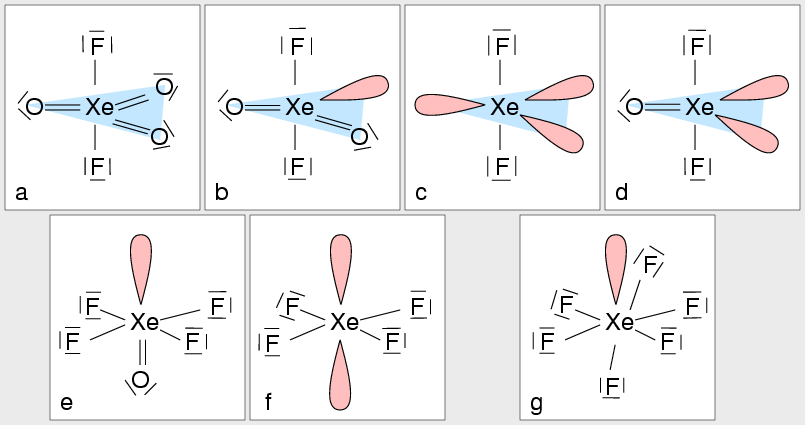 |
| Abb. 3.4.2. Beispiele für die
Molekülstrukturen von Xenonverbindungen nach dem VSEPR-Konzept
‣SVG
|
- XeF2 (Abb. 3.4.2. c)
- Elektronenbilanz: 8von Xe - 2von F = 6 e- = 3 Lone-Pairs (LP)
- Grundgeometrie: 3 LP + 2 F = 5 = trigonale Bipyramide
- Fazit: Die drei Lone-Pairs besetzen die Dreiecksgrundfläche der trigonalen Bipryamide, da hier der
größtmögliche Abstand (Winkel von 120o zwischen den nichtbindenen Elektronenpaare)
vorliegt.
- XeF4 (Abb. 3.4.2. f)
- Elektronenbilanz: 8von Xe - 4von F = 4 e- = 2 LP
- Grundgeometrie: 2 LP + 4 F = 6 = Oktaeder
- Fazit: Die beiden Lone-Pairs besetzen gegenüberliegende Ecken des Oktaeders, da hier der
größtmögliche Abstand (Winkel von 180o zwischen den nichtbindenen Elektronenpaare
vorliegt.
- XeF6 (Abb. 3.4.2. g)
- Elektronenbilanz: 8von Xe - 6von F = 2 e- = 1 LP
- Grundgeometrie: 1 LP + 6 F = 7 = Oktaeder mit Überdachung (oder ähnliches)
- Fazit: Es liegt ein nur schwach verzerrtes Oktaeder vor.
- XeF2O (Abb. 3.4.2. d)
- Elektronenbilanz: 8von Xe - 2von 2 F - 2 von O = 4 e- = 2 LP
- Grundgeometrie: 2 LP + 2 F + 1 O = 5 = trigonale Bipyramide
- Fazit: Das beiden Lone-Pairs und der Sauerstoff besetzen die Dreiecksgrundfläche der trigonalen Bipryamide, da hier der
größtmögliche Abstand (Winkel von 120o zwischen ihnen vorliegt.
- XeF4O (Abb. 3.4.2. e)
- Elektronenbilanz: 8von Xe - 4von F - 2 von O = 2 = 1 LP
- Grundgeometrie: 1 LP + 4 F + 1 O = 6 = Oktaeder
- Fazit: Das Lone-Pair und der Sauerstoffligand stehen einander gegenüber (z.B. axial), da sie den meisten
Platz beanspruchen.
- XeF2O2 (Abb. 3.4.2. b)
- Elektronenbilanz: 8von Xe - 2von F - 4von 2 O = 2 e- = 1 LP
- Grundgeometrie: 1 LP + 2 F + 2 O = 5 = trigonale Bipyramide
- Fazit: Das Lone-Pair und die beiden Sauerstoffliganden besetzen die Dreiecksgrundfläche
der trigonalen Bipryamide, da hier der größtmögliche Abstand vorliegt.
- XeF2O3 (Abb. 3.4.2. a)
- Elektronenbilanz: 8von Xe - 2von F - 6von 3 O = 0 LP
- Grundgeometrie: 0 LP + 2 F + 3 O = 5 = trigonale Bipyramide
- Fazit: Die drei Sauerstoffliganden nehmen die äquatorialen Positionen ein.
Zum Abschluß der Edelgasverbindungen sollen kurz
Bindungsbetrachtungen mit der VB- (veraltet) und der MO-Beschreibung (nur einfachster Fall)
stehen. Als Beispiel wurde XeF2 gewählt.
Beschreibung der Bindung im VB-Modell (! überholt !)
Wegen der Oktettüberschreitung sind die Edelgasverbindungen im VB-Modell nur
durch formale Hybridisierung der s- und p-Zustände mit von d-Orbitale zu beschreiben,
die nach neueren theoretischen und spektroskopischen Untersuchungen
jedoch nicht oder nur minimal möglich ist, da die d-Orbitale energetisch
dazu nicht in der Lage sind.
Formal wurden p-Elektronen der Edelgasatome in d-Orbitale promoviert und so die d-Zuständen an der Bindung
beteiligt, z.B.
- XeF2
- sp3d-Hybridisierung, da 5 Liganden (3 LP und 2 F)
- lineare Geometrie durch lineare Anordnung der pzdz2-Hydridorbitale von Xenon
- XeF4
- sp3d2-Hybridisierung, da 6 Liganden (2 LP und 4 F)
- oktaedrische bzw. quadratisch planare Geometrie
- XeF6
- sp3d3 Hybridisierung, da 7 Liganden (1 LP und 6 F)
- CN 7 bzw. verzerrt oktaedrisch
Beschreibung der Bindung im MO-Modell
Bei der MO-Beschreibung der Bindung werden Molekülorbitale durch die Linearkombination von
Atomorbitalen erzeugt. Dies muß symmetrieangepaßt erfolgen, da Orbitale bzw.
die Kombinationen von Ligand-Orbitalen (die SALCS) verschiedener Symmetrien bzg.
der Molekülsymmetrie (= verschiedener irreduzibler Darstellungen) orthogonal zueinander
sind; zwischen diesen Orbitalen sind keine bindenden oder antibindenden Wechselwirkungen möglich!
Die Konstruktion eines Molekülorbital-Schema erfolgt nach dem Prinzip:
- Bildung der symmetrieadaptierten Linearkombinationen (sog. SALCs) der Ligandorbitale.
- Kombination der SALCs mit den Atomorbitalen des Zentralteilchens.
- Dabei Berücksichtigung der Wechselwirkungen nur zwischen
Orbitalen mit derselben irreduziblen Darstellung (= IR = irreducible representation)
- und nur bei ca. vergleichbarer Energie (Richtwert: maximal 15 eV Energieabstand).
- Elektronegativitätsunterschiede zeigen sich in der Lage der Atomorbitale:
Orbitale von Atomen mit hoher EN liegen tiefer
als die mit kleiner Elektronegativität.
- Je stärker die Wechselwirkung ist, desto stärk ist die Absenkung der bindenden
und die Anhebung der antibindenden Molekülsorbitale relativ zu den
Atomorbitalen, also die Gesamtaufspaltung.
Abbildung 3.4.3. zeigt den exakten gruppentheoretischen Gang der Ermittlung von Molekül- aus Atom-Orbitalen.
 |
| Abb. 3.4.3. Prinzip
der Bestimmung von Moleküorbitalen
‣SVG
|
Beispiel XeF2
In 1. Näherung werden die 3 σ-p-Orbitale, das Xenon-5pz- und die
beiden Fluor-2pz-Orbitale, zu insgesamt drei Molekülorbitalen kombiniert.
Je nach Vorzeichen der AO ergeben sich die folgenden drei Molekülorbitale (s. Abb. 3.4.4.)
- antibindend: +, +, +
- nichtbindend: +,+,- oder +,-,-
- bindend +,-,+
Besetzt man die Molekülorbitale mit vier Elektronen (2 von Xe und je einem von jedem F)
so ergibt sich eine Bindungsordnung von nur 1/2,
da bei zwei Xe-F-Kontakten ist nur ein bindender Zustand populiert ist, die beiden anderen
Elektronen besetzen ein nichtbindendes MO.
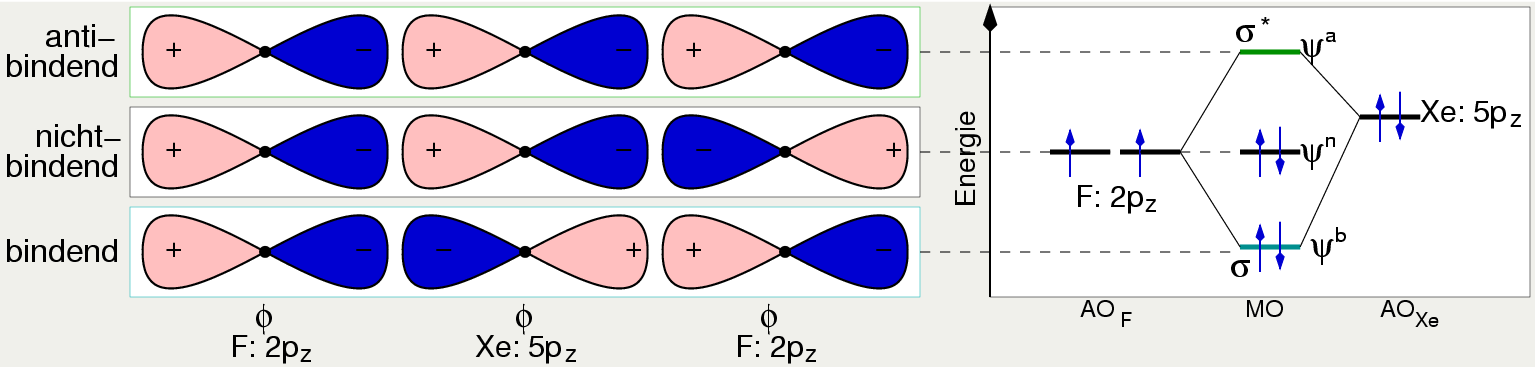 |
| Abb. 3.4.4. MO-Beschreibung
der Bindung in XeF2
‣SVG
|
In der 2., verbesserten Näherung werden die Xe-5s Zustände
mit einbezogen und die Bindungsordnung erhöht sich dadurch wieder etwas:
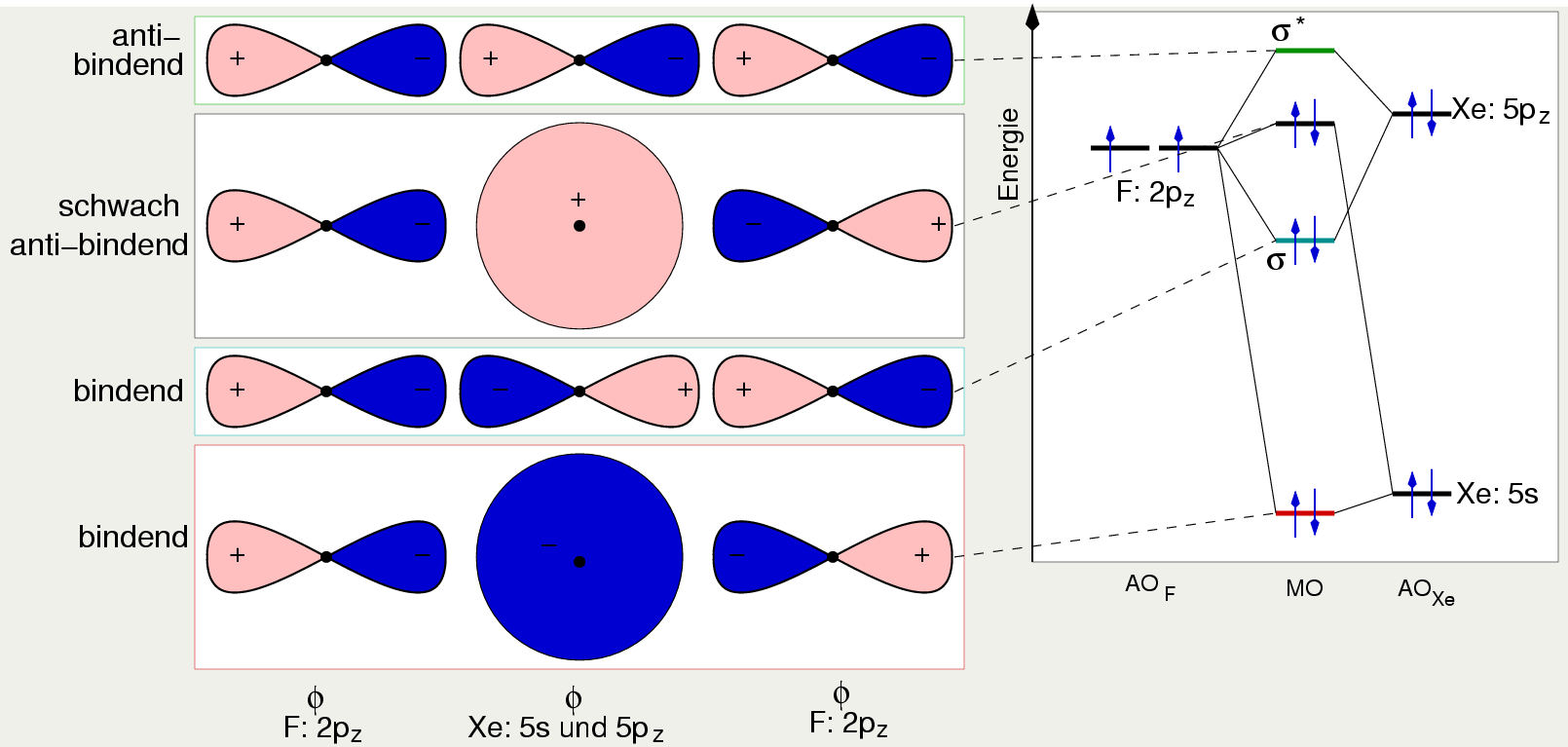 |
| Abb. 3.4.5. MO-Beschreibung
der Bindung in XeF2 (Verbessert)
‣SVG
|





