4.1. Bindung, Konzepte, Radien, Gitterenergie

In der Vorlesung wird der Abschnitt bis zu den Ionenradien in dieser Präsentation wiederholt (Grundkenntnisse AAC und PC).

Ionenkristalle werden immer dann gebildet, wenn die beiden Bindungspartner stark abweichende Elektronegativitäten aufweisen. Der Ionencharakter einer Verbindung läßt sich z.B. nach Pauling (gemäß 1 - e^{-1/4(x_A-x_B)}) ermitteln und liefert die in Tabelle 4.1.1. zusammengestellten Werte.

Verbindung	LiF	MgO	FeO	OsO₄
Ionencharakter nach Pauling	0.9	0.73	0.52	0.35

Tab. 4.1.1. Ionencharakter ausgewählter Salze

Qualitative Betrachtung: Ionische Verbindungen (Salze) werden durch elektrostatische Kräfte zusammengehalten; die Anionen sind von Kationen umgeben und umgekehrt. Eine große elektrostatische Anziehung, d.h. eine große Gitterenergie, wird dabei durch hohe Koordinationszahlen erreicht. Kontakte der Anionen bzw. Kationen untereinander sollten minimal, Kontakte zwischen Anionen und Kationen maximal sein. Gleichzeitg muß lokale elektrostatische Neutralität erreicht sein.

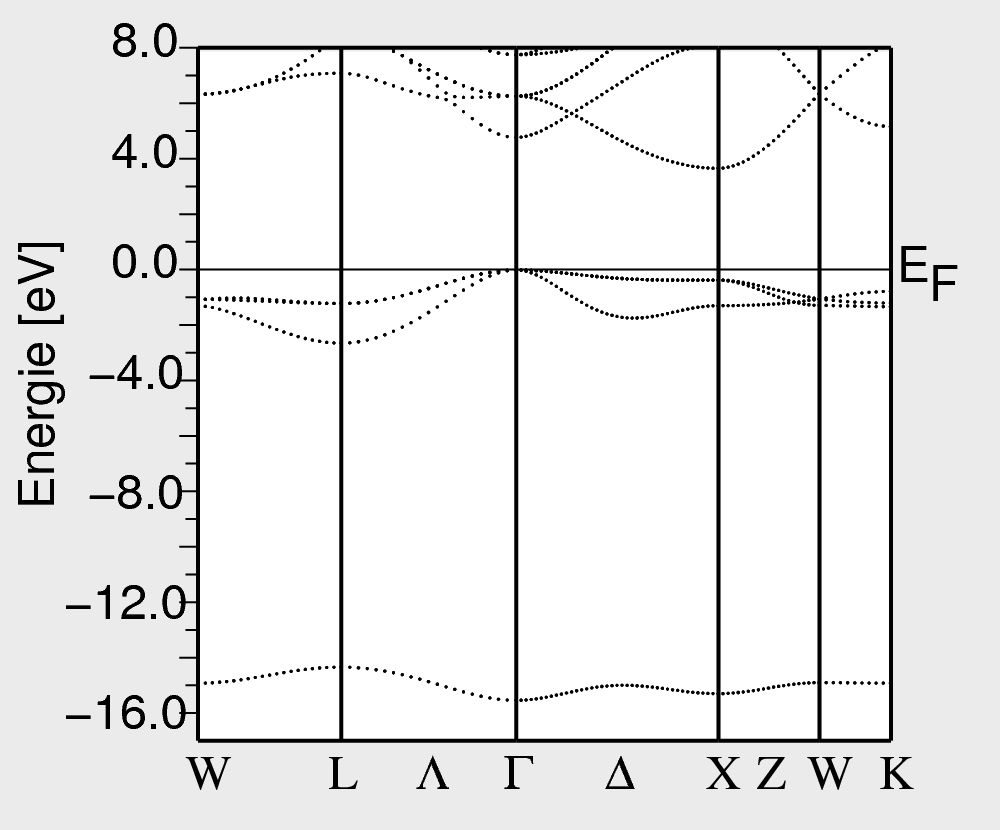
Die elektronischen Strukturen (Zustandsdichten und Bandstrukturen) sind einfach: Alle Bänder sind schmal, das Valenzband besteht aus praktisch atomaren (besetzen) Anionenzuständen, das energetisch weit entfernte Leitungsband aus ebenfalls atomaren (leeren) Kationenzuständen. In Abbildung 4.1.1. ist als Beispiel die Bandstruktur von CaO abgebildet (-15 eV: O-s; VB: O-p; +4 eV: Ca).

Abb. 4.1.1. Berechnete Bandstruktur von CaO ‣SVG

Quantitative Betrachtung: Bei kleinen Drücken verbleibt von der Gibbs-schen freien Energie (G = E - TS + PV) nur die Gibbs-Helmholtz-Energie als wesentlicher Beitrag: F = E - TS. Die innere Energie E des Kristalls besteht dabei aus zwei Anteilen (E = U_L + E_V), dem dynamischen Anteil E_V und der statischen Gitterenergie U_L. Diese Gitterenergie ist wiederum die Summe verschiedener Anteile: (in Klammern typische Prozentangaben zum Beitrag an der gesamten Gitterenergie:)

U_L = E_C (80%) + E_R + E_D (gem. 10-15%) + E_KF (5-10%) + kovalente Bindungsanteile + van der Waals + ..
Die Anteile sind (q = Ladungen, r = Gleichgewichtsabstand, B = Born'scher Abstossungsexponent)

E_C: Coulomb-Wechselwirkung (für 2 Einzelionen unterschiedlicher Ladung nur attraktiv (-): E_c = - (q₁ q₂ e²) / r)
E_D: Dispersionswechselwirkung der Elektronenhüllen (E_D = - A / r⁶)
E_R: elektrostatische Abstoßung der Elektronenhüllen (E_R = B / rⁿ mit n = 5-12 und dem Born'schen Abstossungsexponenten)
E_KF Kristallfeldstabilisierungsenergie (nur bei den Übergangsmetallen)

E_R und E_D werden meist in kombinieren Potentialen (Lenard-Jones, Mie usw.) zusammengefasst und gelten für neutrale Atome/Moleküle entsprechend. A, B usw. sind empirische Parameter!
E_C hängt (unter Vernachlässigung der Ligandenfeldstabilisierungsenergie) nur vom Abstand der Ionen, deren Ladungen sowie dem Strukturtyp ab. Für den Coulombanteil in einem Kristall kann man für die Ionen die Anteile der Umgebung summieren, als Reihe aufschreiben und schliesslich zu einer Konstante für den jeweiligen Strukturtyp, die Madelung-Konstante zusammenfassen:
E_c = - [ { A N₀ q₁ q₂ e²} / {4 π ε r_e} ]
Typische Werte für die Madelungkonstante A sind in Tabelle 4.1.2. zusammengestellt. Die Madelungkonstante gibt also praktisch an, wie viel mehr Energie gewonnen wird, wenn nicht nur ein Ionenpaar, sondern der ganze Kristall (mit gleichen Ionenabständen) gebildet wird.

Strukturtyp	NaCl	Rutil	Anatas	Fluorit
Madelungkonstante A	1.76	2.408	2.400	2.519

Tab. 4.1.2. Madelungkonstanten verschiedener Strukturtypen

U_L kann experimentell z.B. auf der Basis des Born-Haber-Kreisprozeßes bestimmt werden. Danach ist die treibende Kraft für die Bildung eines Ionenkristalls (d.h. die Bildungsenthalpie) zusammengesetzt aus:

ΔH_f = ΔH_M + ΔH_x + ΔH_IE + ΔH_EA + U_L
wobei:

ΔH_f: Bildungsenthalpie
ΔH_M: Sublimationsenergie
ΔH_x: Dissoziationsenergie
ΔH_IE: Ionisierungsenergie
ΔH_EA: Elektronenaffinität
U_L: Gitterenergie

Einige Werte für die Gitterenergien sind in Tabelle 4.1.3. zu finden.

Verbindung	NaCl	MgO	BaO
Gitterenergie U_L [kJ/mol]	-760	-4000	-3200
Schmelzpunkt [^oC]	800	2800	1900

Tab. 4.1.3. Gitterenergien und Schmelzpunkte

Man sieht aus Tabelle 4.1.3, dass die Schmelzpunkte etwa parallel mit der Gitterenergie variieren.

Zur Abschätzung der Größe der Kationen und Anionen gibt es die allgemein weit genutzen Shannon-Radien. Abb. 4.1.5 zeigt die wichtigsten Kationenradien. Anionen: Referenz: Oxid: 140 pm.

Abb. 4.1.2. Kationenradien nach Shannon ‣SVG

Die qualitative Folgerung für die Maximierung der Gitterenergie ist also, dass die Kationen von möglichst vielen Anionen umgeben sein sollten (und umgekehrt) und Kationen und Anionen 'zueinander passen' sollen. Entscheidend für alle weiteren Überlegungen ist, dass die Anionenradien fast immer erheblich größer sind als die Kationenradien.

In der Strukturchemie von Ionenkristallen gibt es hierzu einige empirische Regeln, die sogenannten Pauling-Regeln. Solange wirklich reine Ionenkristalle vorliegen, gelten diese Regeln erstaunlich gut. Sie versagen jedoch, sobald die Ionen von der Kugelform abweichen oder Anteile anderer Bindungstypen (kovalent, metallisch) hinzukommen.

⇦ Inhalt Einleitung Kovalente FK Metalle Ionenkristalle Literatur ⇨

cr_home Metalle Nichtmetalle FK-Chemie Methoden Interm. Phasen Oxide Silicate Strukturtypen