3.1. Übersicht

Vorlagen

Vorlage 3.1: Übersicht: Polarisations- und Transporteffekte (PS, PDF)
Vorlage 3.2: Polarisation: Beispiel Dielektrika (PS, PDF)

Die Anwendungsbereiche von Festkörpern sind sehr vielfältig und letztlich Grund für die Etabilierung des eigenen Faches Materialwissenschaften. Vor der eigentlichen Anwendung steht für uns als Chemiker das Verständnis der Eigenschaften ausgehend von der Festkörperstruktur (inkl. der Baufehler usw.) und der chemischen Bindung bzw. allgemein der elektronischen Struktur. Daneben ist auch die Herstellung der Festkörper für die Materialchemie wichtig. Die generelle Besonderheiten kristalliner Festkörper ist die Tatsache, dass die Atome, Ionen oder Moleküle in wohldefinierter Umgebung vorliegen (definierte (Punkt)-Symmetrie und Abstände). Dies ist z.B. wichtig für die Anwendung der Materialien als Laser bzw. für Lumineszenz-Effekte. Zudem sind kooperative Effekte, die auf einer definierten Wechselwirkung der Teilchen untereinander basieren, nur in Festkörpern möglich (z.B. Wechselwirkung der Elektronenspins in Ferromagneten). Eine weitere Besonderheit von kristallinen Stoffen ist, dass sie bezüglich ihrer Eigenschaften meist nicht isotrop sind. Die Eigenschaften sind also richtungsabhängige (Vektor- und Tensor)-Eigenschaften). Beispiele sind optische Eigenschaften (Indikatrix) oder elektrische Polarisationen bei Piezoelektrika.

Allgemein können folgende Kategorien physikalischer Eigenschaften unterschieden werden:

Polarisations-Effekte oder statischer Response: Polarisationen im Festkörper, der dabei im thermodynamischen Gleichgewicht bleibt, treten auf, wenn ein unendlich hoher Transport-Widerstand bei Änderung/Einwirkung äußerer Parameter/Felder (als Ursache) Änderung der Eigenschaften (als Wirkung) auftritt.
- direkte Polarisation: z.B. B-Feld ? wie ändert sich Magnetisierung ? magn. Suzeptibilität
- indirekte Polarisation: z.B. T-Änderung ? wie ändert sich Magnetisierung ? pyromagn. Effekt
Transport-Effekte oder dynamischer Response: Beim Transport Abweichung vom Gleichgewicht bei Änderung/Einwirkung äußerer Parameter/Felder (Ursache) Fluß von Teilchen, Ladungsträgern usw. (Wirkung) Als Beispiel für die Einwirkung (Ursache) von elektrischen Feldern:
- direkter Transport: z.B. E-Feld ? Ladungstransport ? Elektrodynamik
- indirekter Transport: z.B. E-Feld ? E-Inhalt/Wärme/T ? Peltier-Effekt

3.1.1. Polarisationseffekte

Die Prinzipien sind f¨r diese beiden Gruppen immer gleich. Im Fall der Polarisationseffekte gilt die allgemeine Formel

χ^{YX} = \frac{δ Y}{δ X}

wobei δY f¨r die Wirkung steht, die der Gradient δX (als Ursache), versacht:

\underset{Wirkung}{\underset{︸}{δ Y}} = χ^{YX} \underset{Gradient,Ursache}{\underset{︸}{δ X}}

Bei Änderung einer Grösse X, die selber eine skalare oder vektorielle sein kann, (Ursache) beschreibt die Materialkonstante χ, wie sich Y ändert (Wirkung). Häufig bestehen dabei lineare Abhängigkeiten, besonders bei kleiner, langsamer Änderung. Z.B. bewirkt eine mechanische Spannung eine Deformation (Dehnung), die nach dem Hook'sches Gesetz proportional zueinander sind. χ^XY ist also eine Materialkonstante für die Eigenschaften/Felder/Grössen X und Y. Wenn X und Y richtungsabhängige Grössen sind, ist χ ein Tensor (auch höherer Stufe). Das Verhalten kann auch von der Vorbehandlung abhängen oder nicht proportional sein (Hysterese). χ ist zusätzlich i.A. frequenzabhängig (z.B. Impedanz statt Gleichstromwiderstand). Je nach X und Y haben diese Materialkonstanten unterschiedliche Namen. Man kann nach direkter (in Tab. auf der Diagonale) oder indirekte (Nichtdiagonale) E-Kopplung. Die bunte Tabelle enthält eine Übersicht.

Tab. 3.1.1. Übersicht Polarisations-Eigenschaften von Festkörpern
Ursache X ⇒	Temperatur	elektrisches Feld	Magnetfeld	mechanische Spannung
Wirkung Y ⇓	T [K]	E_i [V/m]	B_i [Vs/m²]	σ_i,j
Entropie	Wärmekapazität	elektrokalorischer Effekt	magnetokalorischer Effekt
S [J/m²s]	$χ^{ST} = c_{p} = \frac{δ S}{δ T} T$	$χ_{i}^{SE} = \frac{δ S}{δ E}$	$χ_{i}^{SB} = \frac{δ S}{δ B}$	$χ_{i, j}^{S σ} = \frac{δ S}{δ σ}$
elektrische Polarisation	pyroelektrischer Effekt	elektrische Suszeptibilität	magnetoelektr. Efffekt	piezoelektrischer Effekt
P_k [Asm²]	$χ_{k}^{P T} = \frac{δ P}{δ T}$	$χ_{i, k}^{P E} = \frac{δ P}{δ E}$	$χ_{i, k}^{P B} = \frac{δ P}{δ B}$	$χ_{i, j, k}^{P σ} = \frac{δ P}{δ σ}$
				piezoelektrische Moduln
Magnetisierung	pyromagnetischer Effekt	elektromagnetischer Effekt	magnetische Suszeptibilität	piezomagnetischer Effekt
M_k [A/m]	$χ_{k}^{M T} = \frac{δ M}{δ T}$	$χ_{i, k}^{M E} = \frac{δ M}{δ E}$	$χ_{i, k}^{M B} = \frac{χ}{μ} = \frac{δ M}{δ B}$	$χ_{i, j, k}^{M σ} = \frac{δ P}{δ σ}$
				piezomagnetische Moduln
mechanische Deformation	thermische Ausdehnung	reziproker piezoelektrischer Effekt (Elektrostriktion)	reziproker piezomagnetischer Effekt	Spannungstensor
ϵ_k,l [A/m]	$χ_{k, l}^{ϵ T} = α_{k, l} = \frac{δ ϵ}{δ T}$	$χ_{i, k, l}^{ϵ E} = \frac{δ ϵ}{δ E}$	$χ_{i, k, l}^{ϵ B} = \frac{χ}{μ} = \frac{δ ϵ}{δ B}$	$χ_{i, j, k, l}^{ϵ σ} = \frac{δ ϵ}{δ B}$
	thermischer Verzerrungstensor	piezoelektrische Moduln	piezomagnetische Moduln	elastische Elastizitätsmoduln

Die obere Reihe der Tabelle enthält die Ursachen, z.B. die Änderung der äußeren Temperatur, des elektrischen (E) und des magnetischen (B) Felds sowie die mechnanische Spannung. In der linken Spalte sind die Änderungen einer bestimmten Materialeigenschaft gelistet. Neben direkt engeriegekoppelten Größen (Diagonale der Tabelle) gibt es auch indirekte Kopplung (Nebendiagonalen), d.h. es sind letztlich beliebige Kombinationen zwischen Ursache und Wirkung denkbar. Durch die Zahl der Indizes ist angedeutet, ob es sich bei den Materialkonstanten um Vektoren (ein Index) Tensoren 2. Stufe (zwei Indizes) oder höherer Stufe (drei, vier .. Indizes) handelt.

1. Spalte (1/X) Änderung der Temperatur (X, ein Skalar) (ohne Wärmeleitung!) führen entweder:
- 1/1 direkt zur Änderung der Entropie S (Y, ebenfalls skalar). Die entsprechende Materialeigenschaft ist die Wärmekapazität c_p, also eine Konstante, da es sich um isotrope Eigenschaften handelt. Wie bei allen Zusammenhängen auf der Diagonalen es dies der erwartete direkte Effekt, direkte E-gekoppelt.
- 1/2 indirekt zu einer elektrischen Polarisation (pyroelektrischer Effekt). $\chi_k$ ist ein Vektor (Tensor 1. Stufe), denn es überführt ein Skalar in einen Vektor. $\chi_k$ hat als bis zu drei Komponenten, bei höherer Symmetrie ggf. auch weniger. Pyroelektrische Effekte treten nur bei Punktgruppen der Klassen C oder D auf, die 222 nicht als Untergruppe haben.
- 1/3 indirekt zu einer Magnetisierung M (pyromagnetischer Effekt). Auch $\chi$ ist ein Tensor 1. Stufe (Vektor).
- 1/4 indirekt zu einer mechanischen Deformation, die in alle Richtungen unterschiedlich ausfallen kann. auch bei linearer Ausdehnung ev. in alle Richtungen unterschiedlich Aus Kugel wird Ellipsoid = 3 Hauptachsen + Orientierung der Hauptachsen damit ist XX ein symmetrischer Tensor 2. Stufe (bis zu sechs unabhängige $\chi$)
2. Spalte (2/X): Anlegen eines elektrischen Feldes E_i (wieder ohne Transport) kann
- 2/1 Y = Entropie S} \underline{elektrokalorischer Effekt}
- 2/2 Y = elektr. Polarisation} (!Diagonalelement!) $\chi$ = elektrische Suszeptibilität (Stärke der Polarisation bei angelegtem E-Feld $\chi_{i,k}$: verknüpft 2 3-dim. Vektoren: 3x3 Tensor 2. Stufe (max. 6 Elemente $DK_{i,j}$)
- 2/3 Y = Magnetisierung M} \underline{elektromagnetischer Effekt} ebenfalls Tensor 2. Stufe
- 2/4 Y = mechanische Verzerrung} Elektrostriktion, reziproker piezoelektrischer Effekt Tensor 3. Stufe: 3x3x3-Matrix, 27 Elemente, aus Symmetriegründen nur max. 18 einzelne Elemente von $\chi$: piezoelektr. Moduln z.B. bei Quarz: nur 2 Moduln
3. Spalte {\bf X=magnetisches Feld $\bf B_i$} alles vergleichbar wie bei E-Feld:
- Y = S magnetokalorischer Effekt
- Y = Polarisation} magnetoelektrischer Effekt
- Y = Magnetisierung} (!Diagonalelement!) magnetische Polarisation $\chi$ magn. Suszeptibilität
- 3/4 Y = mechanische Deformation} rezipr. piezomag. Effekt $\chi$ Tensor 3. Stufe
4. Spalte {\bf X=$\sigma$} Anlegen einer mechn. Spannung $\sigma$ = Tensor 2. Stufe: Normalspannung + Scherspannung Normalspannung: gerader Zug/Druck Scherspannung: kommt dazu
- Y = S-Änderung, Tensor 2. Stufe (erzeugt Skalar)
- Y = elektrische Polarisation, Tensor 3. Stufe (piezoelektr. Moduln)
- Y = Magnetisierung
- Y = Deformation (!Diagonalelement!) Relation Spannung zu Dehnung Tensor 4. Stufe: von $3^4$=81 Komponenten maximal nur 21 verschiedene Einzelelemente: elast. Moduln bzw. Elastizitätsmoduln Untergruppen: Schubmodul, usw. Veranschaulichung/Bild: Elastizitätsmodulkörper

Fazit Tabelle: Die Diagonalelemente beschreiben direkte Eigenschaftsänderungen. Bei Linearität liegt der 'Normalfall' der Physik vor, die Energieart ist gleich. unten: Abweichungen von der Linearität Nebendiagonalelemente beschreiben eher 'unerwartete' Sekundäreffekte, die aber für die Anwendungen sehr interessant sind, da sie Umwandlungen von Energie-Arten ermöglichen. Z.B. bewirkt beim pyroelektrischen Effekte Wärme, T-Gradient eine elektrische Spannung. Beim piezoelektrischen Effekt bewirkt ein elektrisches Feld (Spannung) eine mechanische Deformation.

Abweichungen von der Linearität nennt man in allen Fällen ferroische Eigenschaften. Diese sind praktisch nur für Hauptdiagonale interessant. Die Arten der Wechselwirkung sind in Abbildung 3.1.1. zusammengestellt.

Abb. 3.1.1. Nichtlinearitäten X-Y (ferroische Eigenschaften) ‣ SVG

Für die Spalten 2 bis 4 ergibt sich jeweils für elektrische, magnetische und mechanische Felder:

dia: Hier ist z.B. wegen fehlender Elementarmagnete oder Dipole keine Polarisation möglich. Diamagnetische Stoffe enthalten also keine Atome/Ionen mit ungepaarten Elektronen.
para: Polarisation ist zwar möglich, aber nicht vorhanden. Im Fall para-elektrischer Stoffe sind alle Dipole statistisch verteilt, im Fall para-magnetischer Stoffe sind alle Elementarmagnete (paramagnetische Ionen) statistisch orientiert. Der Para-Zustand ist die Hochtemperaturform (d.h. oberhalb der Curie-Temperatur) aller weiteren, im folgenden genannten Ausrichtungen.
ferro: Hier liegt eine starke Polarisation in eine Richtung vor, die mit einer Hysterese, umkehrbar. Im Fall von ferro-magnetischen Materialien sind die Spins gleich ausgerichtet (z.B. Fe, SmCo₅). Bei ferro-elektrischen Stoffen sind die Dipole gleich ausgerichtet (z.B. NaNO₂) unterhalb 164 ^oC oder KDP). Ferro-elastische Stoffe sind mit Hysterese verformbar (z.B. NdP₅O₁₄).
antiferro: Hier liegt eine gegensinnige Ausrichtung gleicher Spins/Dipole vor. Die Ursache ist eine Kopplung der Polarisationen mit gegensinniger Ausrichtung. Im Fall von magnetischer Polarisation wird dies durch Superaustausch bewirkt, bei elektrischer Polarisatation z.B. durch H-Brücken. Es resultiert damit keine resultierende Gesamtpolarisation und auch keine Hysterese. Im Fall antiferro-magnetischer Stoffe sind die Spins entgegengesetzt ausgerichtet (z.B. NiO), bei antiferro-elektrischen Stoffen sind die Dipole entgegengesetzt ausgerichtet (z.B. NH₄[H₂PO₄] = ADP).
ferri: Hier liegt zwar ebenfalls eine gegensinnige Ausrichtung vor, die Einzelspins/dipole haben aber unterschiedlich große Momente. Makroskopisch verhalten sich die Stoffe wie ferroische Materialien, zeigen also z.B. Hysterese. Wichtige ferrimagnetische Materialien sind Ferrit wie z.B. CoFe₂O₄, Bi₄Ti₃O₁₂ ist ein Ferri-Elektrikum.

Alle ferroischen Eigenschaften sind in einheitlicher Weise temperaturabhängig (s. Abb. 3.1.X)

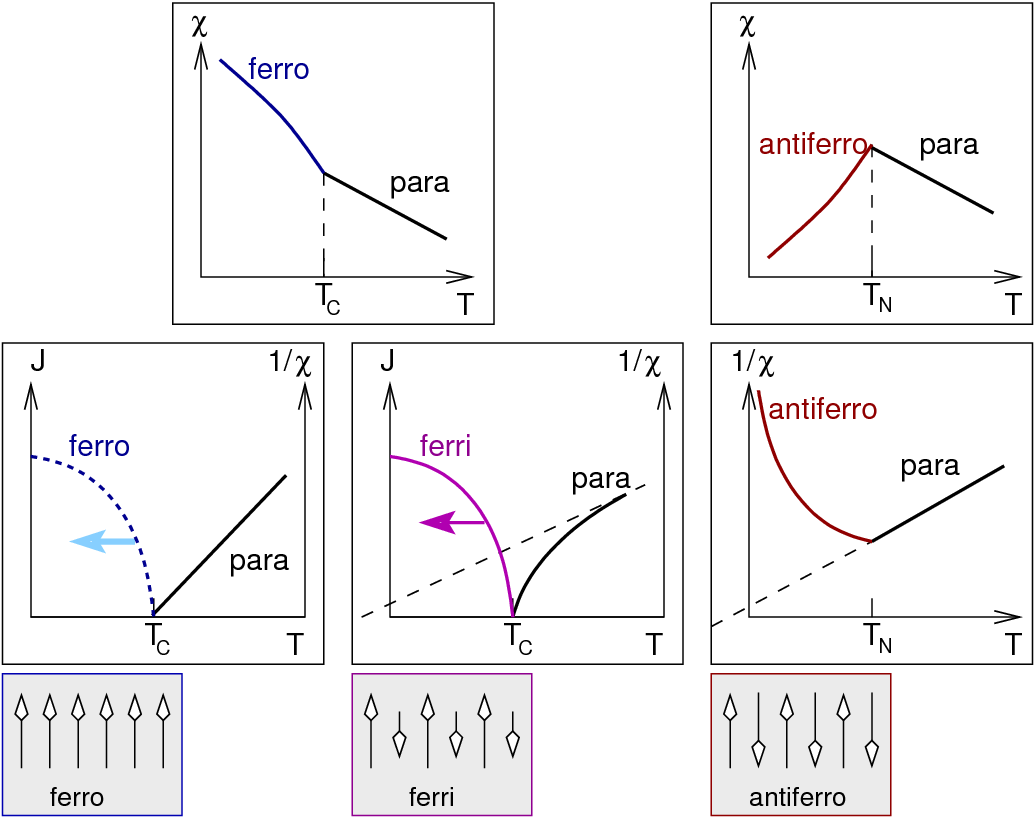
Abb. 3.2.2. Temperaturabhängigkeit ferroischer Eigenschaften ‣ SVG

Die Temperaturen, oberhalb derer die ferroischen Eigenschaften verschwinden, nennt man im Fall von ferro und ferri Curie, im Fall des antiferro-Verhalten Neel-Temperatur.

3.1.2. Transporteffekte

Für Transporteffekte (dynamischer Response, Nicht-Gleichgewicht) gilt die allgemeine Formel:

\underset{Fluss}{\underset{︸}{J_{Y}}} = - \underset{Transport-Koeff.}{\underset{︸}{a^{Y X}}} \underset{Gradient}{\underset{︸}{\nabla X}}

Gradient bzw. äußeres Feld Transport im FK mathematisch: $a_{i,y}$: symmetrischer Tenor 2. Stufe (Onsager) max. 6 Elemente meist einfache Proportionalität Diagonalglieder einfache Physik Nebendiagonal-Glieder exotischer Die entsprechende tabellarische Übersicht findet sich in Tabelle XXY.

Tab. 3.1.2. Übersicht Transport-Eigenschaften von Festkörpern
∇X ⇒	Gradient
Fluss J_Y⇓	∇T [K/m]	∇p [kg/m²s²]	∇N_v [m^-4]	∇U [V/m]
Wärme Q	Wärmeleitung	mechanokalorischer Effekt	Diffusionswärme	Peltier bzw. 2. Benedicks-Effekt
[J/m²s]	$\frac{d Q}{d t} = - λ A \frac{d T}{d z}$	-	-	-
Masse m	thermomechanischer Effekt	Massetransport	Diffusionsdruck	-
[kg/m²s]	-	$\frac{d m}{d t} = \frac{konst .}{η} \frac{d p}{d z}$	-	-
-	-	Viskosität (Hagen-Poiseuille Gesetz)	-	-
Teilchenzahl N	Thermodiffusion	Druckdiffusion	Diffusion	Elektrophorese
[m^-2s^-1]	-	-	$\frac{d N}{d t} = - D \frac{d N}{d z}$	-
-	-	-	Diffusionskonstante (1. Fick'sches Gesetz)	-
Ladung q	Seebeck/1. Benedicks-Effekt	-	Strömungsstrom	Elektrizitätsleitung
[A/m²]	-	-	-	$\frac{d q}{d t} = σ A \frac{d U}{d z}$
-	-	-	-	Leitfähgikeit (Ohm'sches Gesetz)

Die obere Reihe beschreibt einen Gradienten (in Richtung z) der Feldgrösse X, z.B.

einen Temperatur-Gradienten
einen Druckunterschied
einen Konzentrationsgradienten
einen Potentialgradient (elektrische Spannung)

In der linken Spalte sind die resultierenden Ströme/der Transport $J_Y$ (Einheit pro Zeit und pro Fläche) angetragen. Auf der Diagonale liegen die jeweils naheliegende Transporteffekte, bei Linearität ergeben sich die bekannten physikalische Transportgesetze:

Wärmeleitung resuliert aus einem Ausgleich von Temperaturunterschieden als Gradient. Die Proportionalitätskonstante ist die Wärmeleitfähigkeit \lambda.
Masse-Transport resultiert aus einem Ausgleich von Druckunterschieden als Gradient. Die Proportionalitätskonstante ist die Viskosität, das Gesetz ist das Hagen-Poiseuille-sche Gesetz.
Teilchen-Transport resultiert aus einem Ausgleich von Konzentrationsgradienten. Die Proportionalitätskonstante ist die Diffusionskonstante, das Gesetz ist das 1. Fick'sches Gesetz.
Stromfluß, d.h. Ladungs-Transport resultiert aus einem Ausgleich von Potentialgradient (d.h. elektrischer Spannung). Die Proportionalitätskonstante ist der spezifischer elektrische Widerstand, das Gesetz das Ohm'sches Gesetz.

Auf der Nebendiagonale finden sich eher ungewöhnliche Sekundäreffekte die z.T. nur relativ exotisch sind. Nur einige davon sind wichtig:

Kommt es beim Anlegen elektrischer Spannung (Gradient) zum Wärmetransport, dann tritt der sog. Peltier-Effekt auf, der z.B. für Kühlaggregate genutzt werden kann. Die zugehörige Materialklasse nennt man Thermoelektrika.
Kommt es aufgrund von Temperaturunterschieden zum Ladungstransport (Stromfluß), zeigt das Material den Seebeck-Effekt.

←

Inhalt

1. Bau + Strukturen

2. Reaktionen + Synthesen

3. Eigenschaften + Anwendungen

Oxide