|
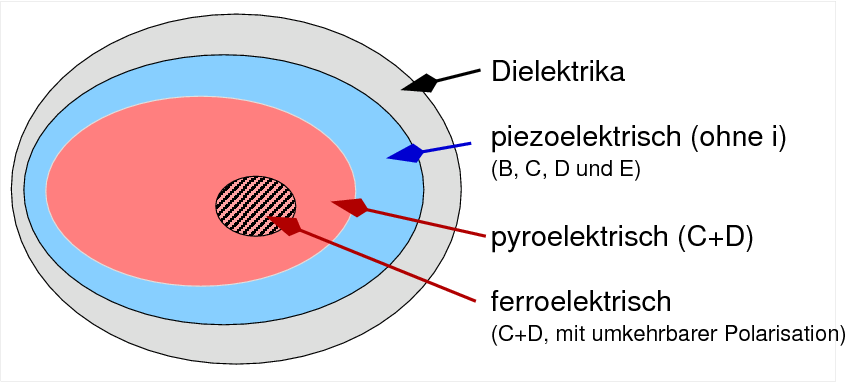
| Abb. 3.2.1. Kristallographische Voraussetzungen für besondere Effekte bei Dielektrika ‣ SVG |
| cr_home | Metalle | Nichtmetalle | Strukturchemie | Methoden | Interm. Phasen | Oxide | Silicate | Strukturtypen |
| ← | Inhalt | 1. Bau + Strukturen | 2. Reaktionen + Synthesen | 3. Eigenschaften + Anwendungen | → |
Vorlagen

|
| Abb. 3.2.1. Kristallographische Voraussetzungen für besondere Effekte bei Dielektrika ‣ SVG |
|
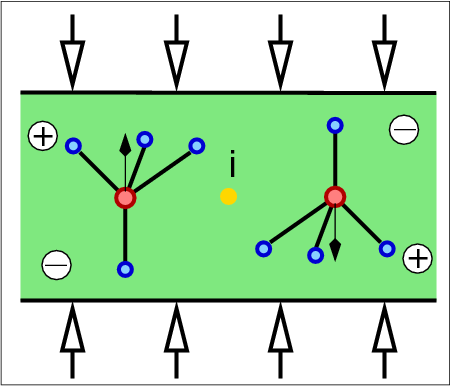
| Abb. 3.2.2. Inversionzentren und Piezoelektrizität schliessen sich aus ‣ SVG |
|
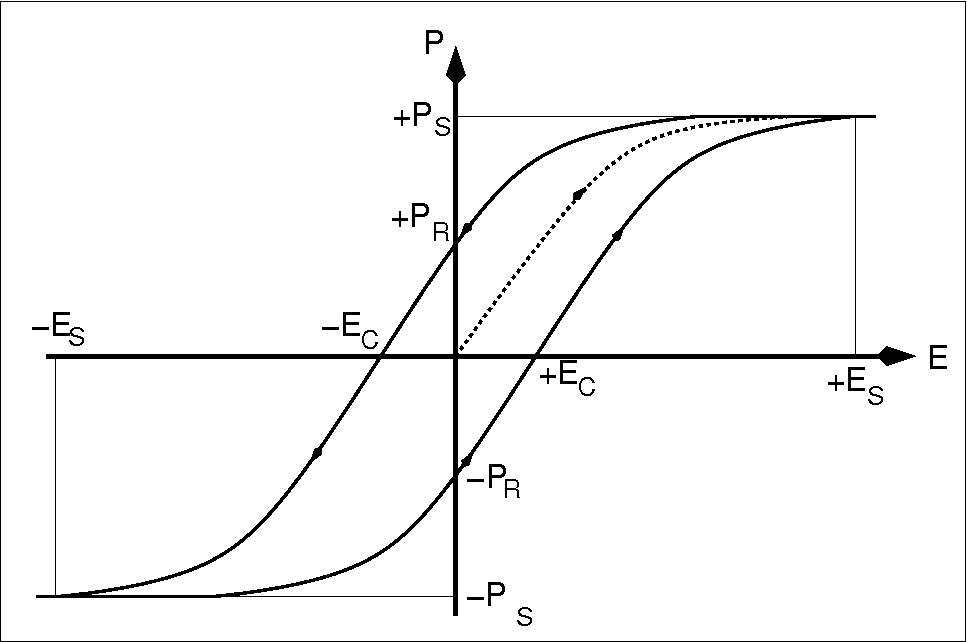
| Abb. 3.2.3. Hysterese der Polarisation bei Ferroelektrika ‣ SVG |
| Verbindung | Tc [oC] | ferroelektrisch | antiferro-elektr. | ferrielektrisch |
|---|---|---|---|---|
| BaTiO3 | 120 | x | ||
| KNbO3 | 434 | x | ||
| NaNbO3 | 638 | x | ||
| LiNbO3 | 1210 | x | ||
| PbZrO3 | 233 | x | ||
| Pb(ZrxTi1-x)O3 (PZT) | x | x | ||
| Bi4Ti3O12 | 675 | - | - | x |
| Gd2(MoO4)3 (GMO) | 159 | x | - | - |
| NaNO2 | 164 | x | - | - |
| KH2PO4 (KDP) | -150 | x | - | - |
| NH4H2PO4 (ADP) | -125 | - | x | - |
|
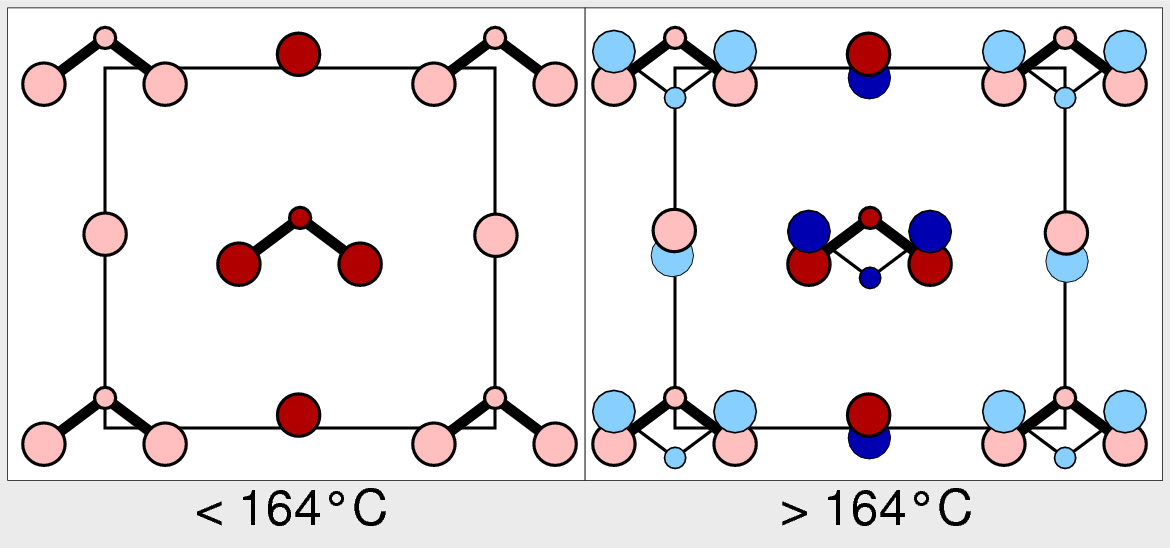
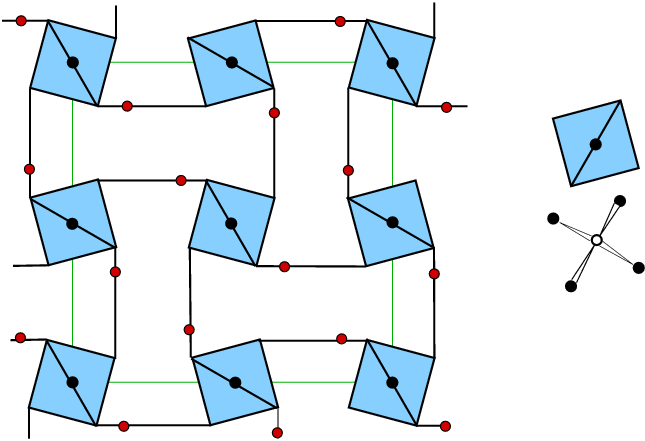
| Abb. 3.2.4. Polarisation bei Natriumnitrit ‣ SVG |
|
| Abb. 3.2.2. Polarisation bei Kaliumdihydrogenphosphat (KDP) ‣ SVG |

|
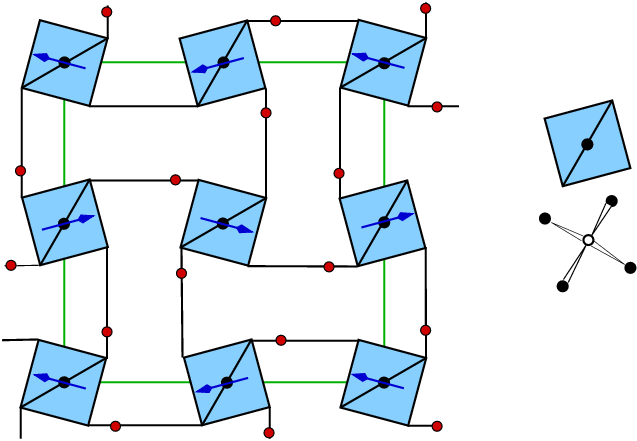
| Abb. 3.2.2. Widerstand von PTC-Thermistoren ‣ SVG |
|
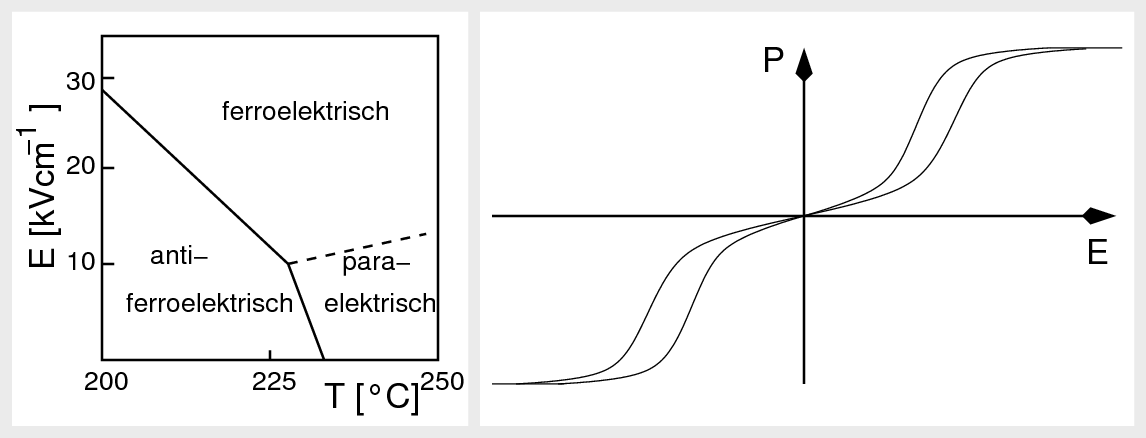
| Abb. 3.2.X. Polarisation in NH4H2PO4> ‣ SVG |
|
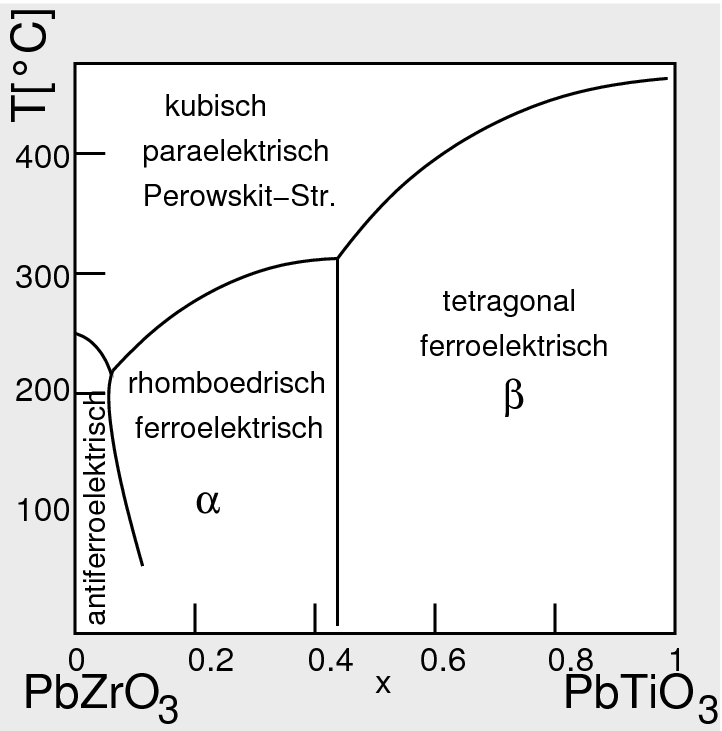
| Abb. 3.2.X. Doppelhysterese von PbZrO3 ‣ SVG |
|
| Abb. 3.2.X. Phasendiagramm von PZT-Keramiken ‣ SVG |
|
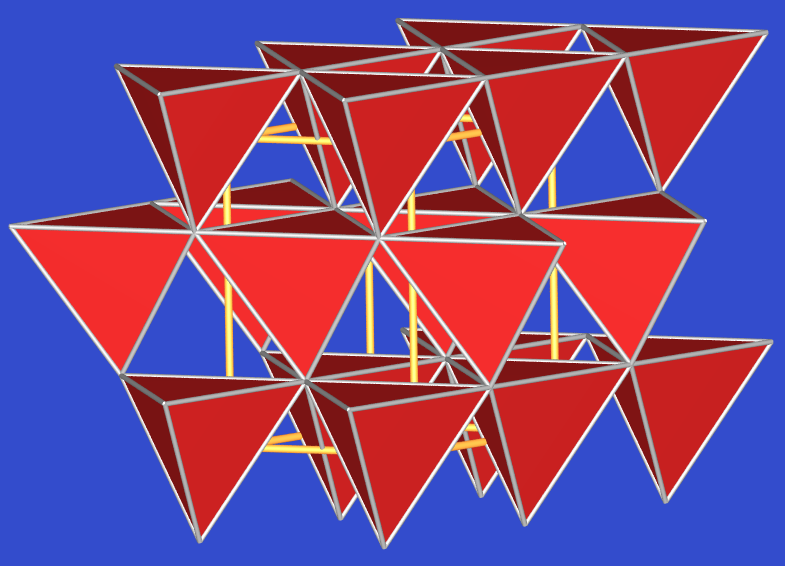
| Abb. 3.2.X. Kristallstruktur von ZnO (Wurtzit) ‣ VRML |
|
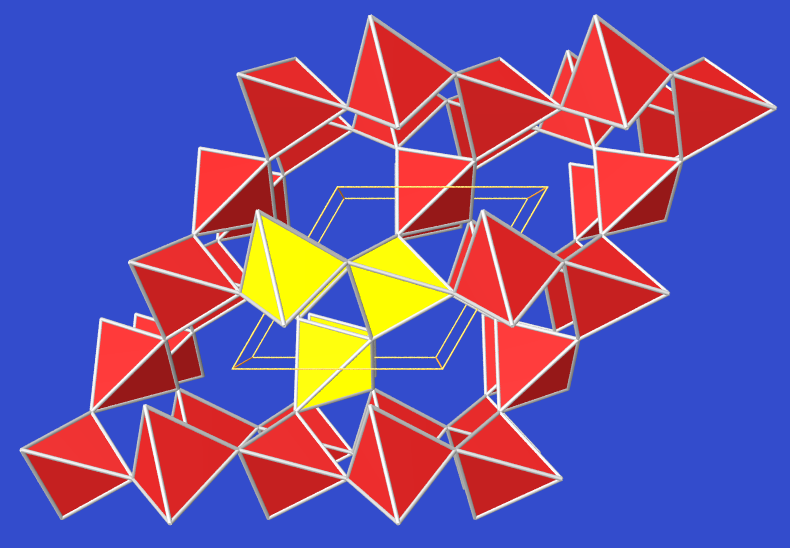
| Abb. 3.2.X. Kristallstruktur von Quarz ‣ VRML |
| Ion | Elektronenkonfiguration | Grundterm | mu_s/mu_B berechn. . | mu_s/mu_B exp. |
|---|---|---|---|---|
| V4+ | d1 | 2D3/2 | 1.73 | 1.8 |
| V3+ | d2 | 3F2 | 2.83 | 2.8 |
| V2+, Cr3+ | d3 | 4F3/2 | 3.87 | 3.8 |
| Mn3+, Cr2+ | HS-d4 | 5D0 | 4.9 | 4.9 |
| Mn2+, Fe3+ | HS-d5 | 6S5/2 | 5.92 | 5.9 |
| Fe2+ | HS-d6 | 5D4 | 4.9 | 5.4 |
| Substanz | mu_r | B_s [T] | H_c [A/m] | M_R [T] | B $\cdot$ H [TA/m] |
|---|---|---|---|---|---|
| SmCo5 | 760 000 | 0.95 | 200 000 | ||
| Nd_2Fe_{12}B | 880 000 | 1.2 | 360 000 | ||
| BaFe_{12}O_{19} | 190 000 | 0.4 | 20 000 | ||
| Fe | 5 000 | 2.14 | 72 | ||
| 45-Permalloy (Fe/Ni) | 25 000 | 1.6 | 20 | klein | |
| B2 Ferroxcube $(Ni,Zn)Fe_2O_4$ | 0.3 | ||||
| $\gamma$-$Fe_2O_3$ | 30 000 | ||||
| $\gamma$-$Fe_2O_3$ Co-dot. | |||||
| CrO2 | 110 000 | ||||
| Fe | 75 000-130 000 | ||||
| Fe/Co (70/30) | 90 000-160 000 | ||||
| Co/Pt/Cr/B |
| $T_{C/N} [K]$ | ferro | antiferro | |
|---|---|---|---|
| Fe | 1043 | x | |
| Ni | 631 | x | |
| Co | 1404 | x | |
| Nd_2Fe_{12}B | 583 | x | |
| SmCo_5 | 998 | x | |
| Mn | 95 | x | |
| Cr | 313 | x |
| A3 | B2 | X3 | Magnetismus | |
|---|---|---|---|---|
| Grossular | Ca3 | Al2 | Si3 | - |
| Uvarovit | Ca3 | Cr2 | Si3 | - |
| Pyrop | Mg3 | Al2 | Si3 | - |
| Andradit | Ca3 | Fe2 | Si3 | - |
| YIG | Y3 | Fe2 | Fe3 | ferri |
| ← | Inhalt | 1. Bau + Strukturen | 2. Reaktionen + Synthesen | 3. Eigenschaften + Anwendungen | → |
| cr_home | Metalle | Nichtmetalle | Strukturchemie | Methoden | Interm. Phasen | Oxide | Silicate | Strukturtypen |