|
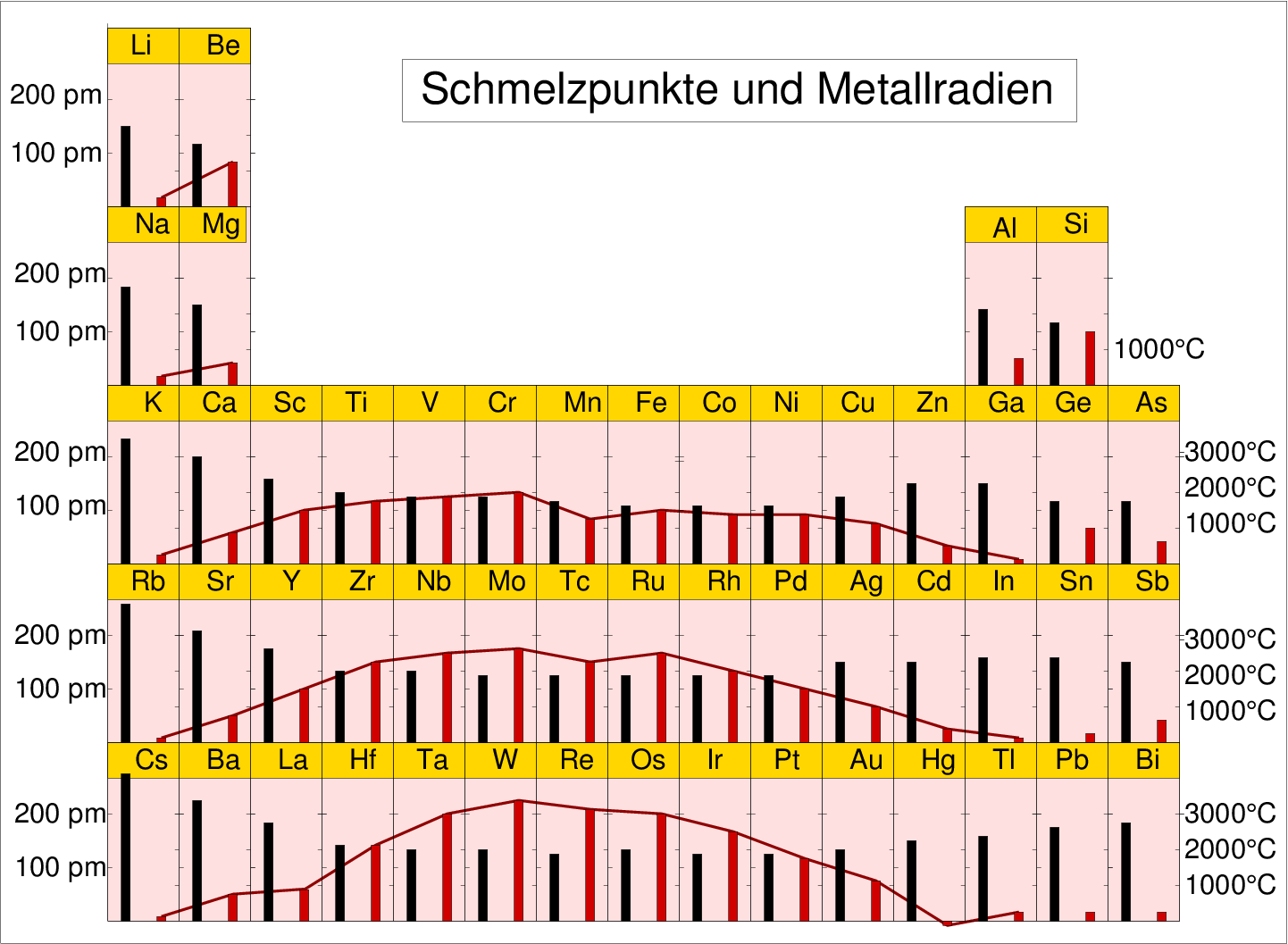
| Abb. 2.1.1. Schmelzpunkte und Atomradien ‣SVG ‣VRML-PSE |
| cr_home | Metalle | Nichtmetalle | Strukturchemie | Festkörperchemie | Oxide | Silicate | Strukturtypen |
| ⇦ | Inhalt | Kap. 1 | Kap. 2 | Kap. 3 | Kap. 4 | Kap. 5 | Kap. 6 | Kap. 7 | Kap. 8 | Lit. | ⇨ |
| Element | oxidiert | reduziert | E [V] | |
| Fluor (F) | F2 | + 2e- ⟶ | 2 F- | +2.87 V |
| Schwefel | S2O82- | + 2e- ⟶ | 2 SO42- | +2.00 V |
| Sauerstoff | H2O2 + 2 H3O+ | + 2e- ⟶ | 4 H2O | +1.78 |
| Gold (Au) | Au+ | + e- ⟶ | Au | +1.69 V |
| Au3+ | + 3e- ⟶ | Au | +1.50 V | |
| Au3+ | + 2e- ⟶ | Au+ | +1.40 V | |
| Chlor (Cl) | Cl2 | + 2e- ⟶ | 2Cl- | +1.36 V |
| Brom (Br) | Br2 | + 2e- ⟶ | 2Br- | +1.07 V |
| Platin (Pt) | Pt2+ | + 2e- ⟶ | Pt | +1.12 V |
| Silber (Ag) | Ag+ | + e- ⟶ | Ag | +0.80 V |
| Eisen (Fe) | Fe3+ | + e- ⟶ | Fe2+ | +0.77 V |
| Iod (I) | I2 | + 2e- ⟶ | 2I- | +0.53 V |
| Kupfer (Cu) | Cu+ | + e- ⟶ | Cu | +0.52 V |
| Cu2+ | + 2e- ⟶ | Cu | +0.34 V | |
| Cu2+ | + e- ⟶ | Cu+ | +0.16 V | |
| Wasserstoff (H) | 2H+ | + 2e- ⟶ | H2 | 0 V |
| Blei (Pb) | Pb2+ | + 2e- ⟶ | Pb | -0.13 V |
| Zinn (Sn) | Sn4+ | + 2e- ⟶ | Sn2+ | -0.15 V |
| Nickel (Ni) | Ni2+ | + 2e- ⟶ | Ni | -0.23 V |
| Cadmium (Cd) | Cd2+ | + 2e- ⟶ | Cd | -0.40 V |
| Eisen (Fe) | Fe2+ | + 2e- ⟶ | Fe | -0.45 V |
| Nickel (Ni) | NiO2+2 H2O | + 2e- ⟶ | Ni(OH)2 + 2 OH- | -0.49 V |
| Zink (Zn) | Zn2+ | + 2e- ⟶ | Zn | -0.76 V |
| Wasserstoff (H) | 2 H2O | + 2e- ⟶ | H2 + 2 OH- | -0.83 V |
| Chrom (Cr) | Cr2+ | + 2e- ⟶ | Cr | -0.91 V |
| Niob (Nb) | Nb3+ | + 3e- ⟶ | Nb | -1.099 V |
| Vanadium (V) | V2+ | + 2e- ⟶ | V | -1.175 V |
| Mangan (Mn) | Mn2+ | + 2e- ⟶ | Mn | -1.19 V |
| Zinn (Sn) | Sn2+ | + 2e- ⟶ | Sn | -1.38 V |
| Aluminium (Al) | Al3+ | + 3e- ⟶ | Al | -1.66 V |
| Titan (Ti) | Ti2+ | + 2e- ⟶ | Ti | -1.77 V |
| Magnesium (Mg) | Mg2+ | + 2e- ⟶ | Mg | -2.37 V |
| Natrium (Na) | Na+ | + e- ⟶ | Na | -2.71 V |
| Calcium (Ca) | Ca2+ | + 2e- ⟶ | Ca | -2.82 V |
| Kalium (K) | K+ | + e- ⟶ | K | -2.92 V |
| Caesium (Cs) | Cs+ | + e- ⟶ | Cs | -2.92 V |
| Lithium (Li) | Li+ | + e- ⟶ | Li | -3.04 V |
| Tab. 2.1.1. Standardpotentiale ausgewählter Redoxpaare |
Daneben ist für die Stabilität sehr wichtig, ob eine (Oxid)-Deckschicht entsteht bzw. wie diese beschaffen ist (s. z.B. bei Al oder Mg). Für die Übergangsmetalle sind zahlreiche Oxidationsstufen charakteristisch. Die Chemie dieser Metalle ist entsprechend vielfältig und wird zusätzlich interessant durch die Bildung von Koordinationsverbindungen mit Elektronenpaardonoren (Liganden).

|
| Abb. 2.1.1. Schmelzpunkte und Atomradien ‣SVG ‣VRML-PSE |
Die Abbildung 2.1.1. zeigt den Gang der Schmelzpunkte (der in etwa dem der Siedepunkte entspricht) im Periodensystem. Maximale Schmelzpunkte liegen in jeder Periode bei halb gefüllten d-Schalen vor (Cr, Mo und W; 6. NG). Ausgehend von dieser Gruppe nehmen Schmelz- und Siedepunkte nach rechts und links stetig ab. Weit rechts im Periodensystem steigen die Schmelzpunkte wieder leicht an, da hier zunehmend kovalente Bindungsanteile (und damit hohe Bindungsenergien) vorliegen. Die Dichte der echten Metalle verläuft etwa umgekehrt zu den Schmelzpunkten. Sie hängt bei den einfachen Metallpackungen den Atommassen) ab. Damit verlaufen hier auch die Schmelzpunkte umgekehrt zu den Atomradien und parallel zur Dichte.
Die Gitterenergie (Kohäsionsenergie) der metallischen Elemente zeigt (wie auch der Verlauf der stabilen Oxidationsstufen, s. Kap. X.X. der Vorlesung Chemie der Metalle) beim Gang von links nach rechts im Periodensystem einen ungew"ohnlichen Verlauf. Die Gitterenergien steigen bis zur Mitte jeder Elementgruppe und fallen dann zum Ende jeder d-Elementreihe wieder ab. Daraus folgt die Beobachtung, dass die Metallradien bis zu Hälfte der Gruppe fallen und dann zum Ende der Periode wieder steigen. Dies ist gekoppelt mit den oben beschriebenen Maxima der Schmelz- und Siedepunkte bei den mittleren Elementen jeder d-Gruppe.
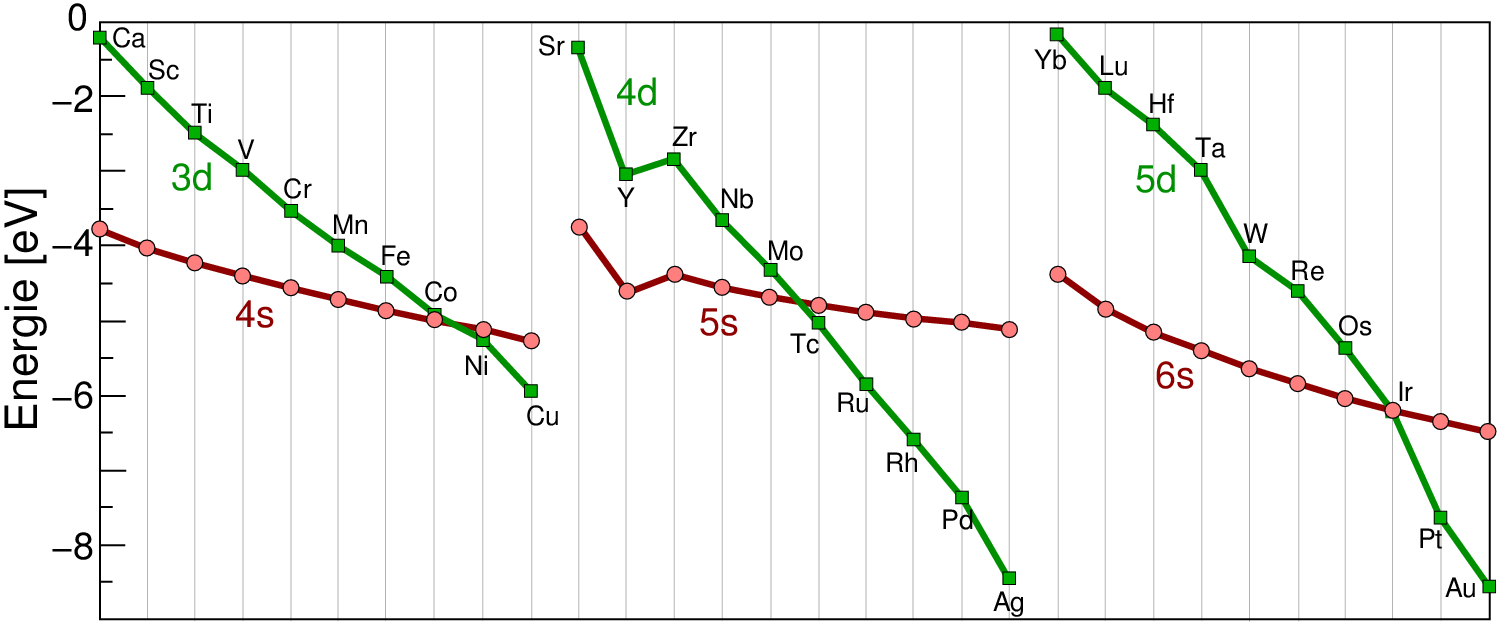
Zur Erklärung dieser Beobachtung muss bedacht werden, dass die s- und p-Zustände in den Übergangsmetallen gemeinsam breite Bänder ausbilden, da die radiale Dichteverteilungen der Atome vergleichbar sind. Dagegen sind die bei den Übergangsmetallen ebenfalls zum Valenzbereich geh"orenden (n-1) d-Elektronen energetisch zwar ebenfalls vergleichbar, diese Orbitale sind jedoch deutlich kernnäher als die s- und p-Zustände der darunterliegenden d-Schale. Betrachtet man zunächst nur die Lage der (n-1) d- und der n s-Zustände, so ergibt sich aus Rechnungen der freien Atome das in Abbildung 2.1.2. gezeigte Bild:
|
| Abb. 2.1.2. Energetische Lage der (n-1) d- und der n s-Orbitale bei freien Übergangsmetall-Atomen ‣SVG |
Die Kernladungszahl Z steigt in jeder d-Reihe von links nach rechts im Periodensystem. Daraus folgt für die Atome selber, dass sowohl die Energien der n s- als auch die der (n-1) d-Niveaus in dieser Richtung fallen, die radialen Dichten \rho und die Wellenfunktionen kontrahieren. Allerdings schrumpften bzw. sinken die (n-1) d--Zustände stärker als die n s-Niveaus, da die Kern-näherenden d-Zustände stärkere Auswirkung der steigenden Kernladung 'spüren'. Verglichen mit den 3d-Zuständen fallen die 4/5d-Orbitale stärker, da weniger d-d-Abstoßung in der ausgedehnteren Schale auftritt. Vor allem die 6s-Zustände fallen aufgrund relativistischer Effekte überproportional. Damit ändert sich über jede "Übergangsmetallreihe der Abstand der s von den d-Niveaus: links: $\Delta_{\it s-d}$ stark negativ Mitte: $\Delta_{\it s-d}$ klein \\ rechts $\Delta_{\it s-d}$ positiv \\

|
| Abb. 2.1.3. Schematische Darstellung der DOS in elementaren Übergangsmetallen ‣SVG |

|
| Abb. 2.1.4. Zustandsdichten der Metalle Ti, Mo und Ag (FP-LAPW-Rechnung, 1000 k-Puntke) ‣SVG |
Die Änderungen der atomaren Energien machen sich nun bei der elektronische Struktur der reinen Metalle in etwas wie folgt bemerkbar: (genauer s.u.) Die n s/ p und (n-1) d-Zustände sind nicht im Core. s- und p-Zustände liegen bei ähnlichen Energien, hybridisieren und entsprechen insgesamt dem NFE-Ansatz (s. Kap. 2.2). Die (n-1)d liegen als 'Block' im s/p-Bandbereich. Die Lage dieses Blocks relativ zu s/p-Band-Unterkante sehr ähnlich wie Verlauf der Atomniveaus (s.o.):
|
|
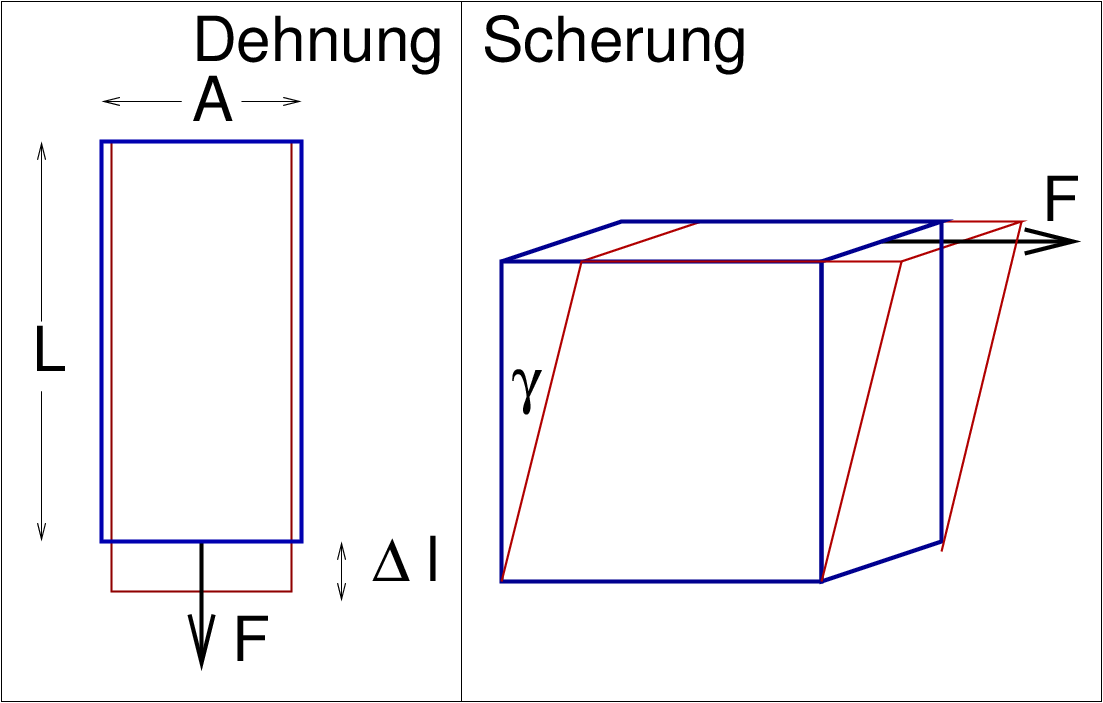
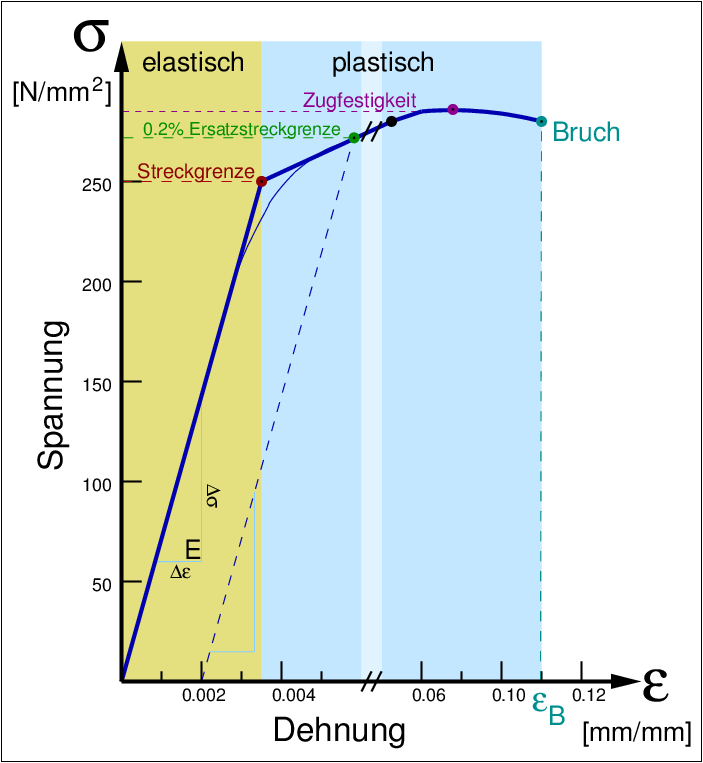
| Abb. 2.1.2. Mechanische Eigenschaften (links: elastisch, rechts: plastisch) ‣SVG, elastisch und ‣SVG, plastisch | |
Die mechanischen Eigenschaften müssen unterschieden werden in:
| Elastizitätsmodul | Zugfestigkeit | Bruchdehnung | |
| E [kN/mm2]=[GPa] | σF [N/mm2]=[MPa] | εB [%] | |
| Al | 70 | 75-110 | 7 |
| Dural | 73 | 420-500 | 22 |
| α-Fe | 218 | 180-210 | 50 |
| V2A-Stahl | 195 | 500-750 | 40 |
| Cu (rein) | 100-130 | 200 | 40 |
| Cu (kaltgezogen) | 126 | 350 | 5 |
| Au | 81 | 140 | 50 |
| Pb | 16.1 | 12 | . |
| Mg | 44.8 | 116 | . |
| Ir | 530 | . | . |
| Si | 100 | . | . |
| Al2O3 | 379.3 | . | . |
| Beton | 27-45 | 1.6-5.2 | . |
| Tab. 2.1.1. Mechanische Eigenschaften einiger Metalle (inkl. Vergleiche) |
Am Beispiel des Aluminiums zeigt sich die Abhängigkeit der Elastizitätsgrenze von der Vorbehandlung der Probe. Indium und Zinn weisen geringe Härte, ein geringes Schubmodul aber eine hohe Elastizitätsgrenze auf. Molybdän ist besonders hart und hat ein hohes Elastizitätsmodul und hohe Zugfestigkeit.
Neben den obengenannten Größen gibt es weitere, technisch im Detail definierte Meßgrößen für die mechanischen Eigenschaften von Metallen:
|
| Abb. 2.1.X. Übersicht Magnetmaterialien‣SVG |
| TC bzw. TN [K] | Sättigungs- Magnetisierung [T] | |
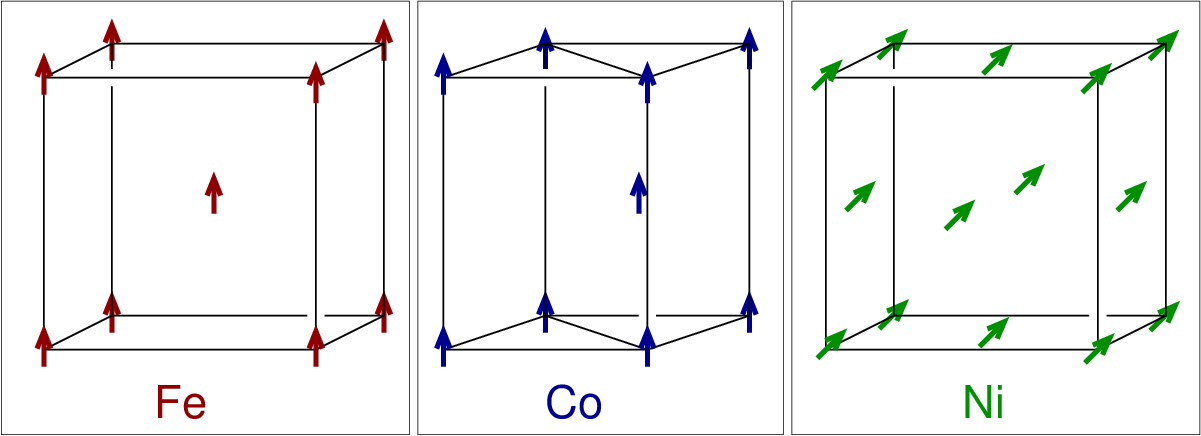
| Fe | 1043 | 1.740 |
| Co | 1388 | 1.446 |
| Ni | 627.2 | 0.510 |
| Gd | 292.5 | 2.060 |
| Cr | 308 | - (AFM) |
| Tab. 2.1.3. Magnetische Eigenschaften einiger Metalle |
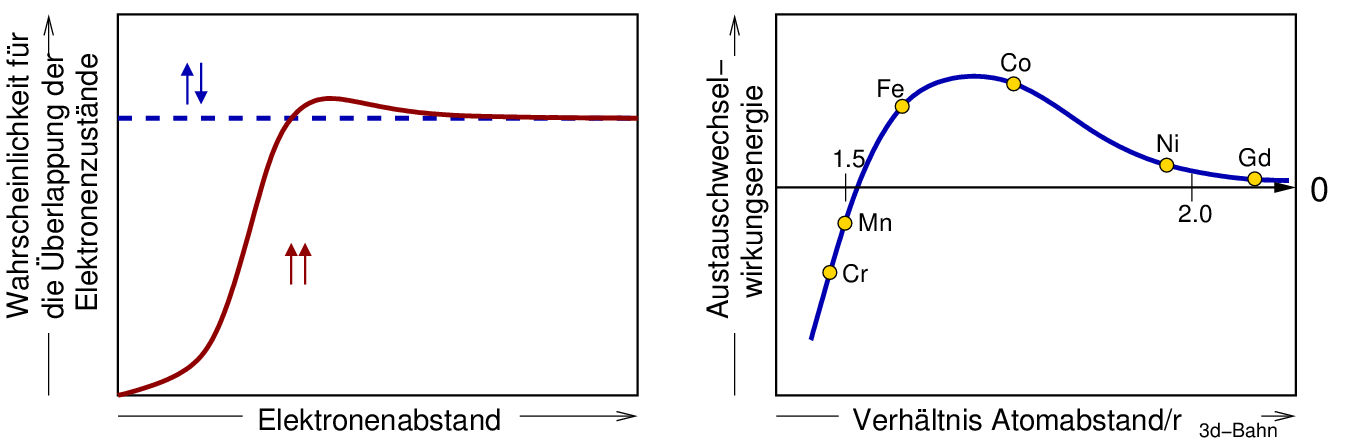
Die ferromagnetische Orientierung benachbarter Spins in einigen Metalle wir vereinfacht mit der sog. Bethe-Slater-Kurve symbolisiert (s. Abb. 2.1.X).
|
| Abb. 2.1.X. Übersicht Magnetmaterialien‣SVG |
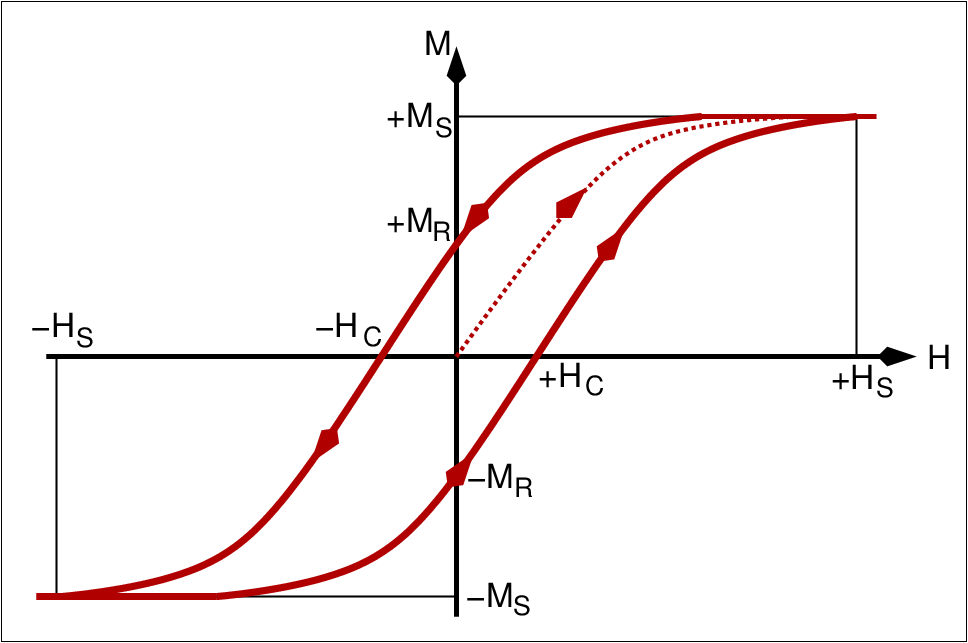
Für die Anwendungen ist die Hysterese relevant. Kenngrössen sind ...
(Hysterese, Sättigungsmagnetisierung)
|
| Abb. 2.1.X. Übersicht Magnetmaterialien‣SVG |
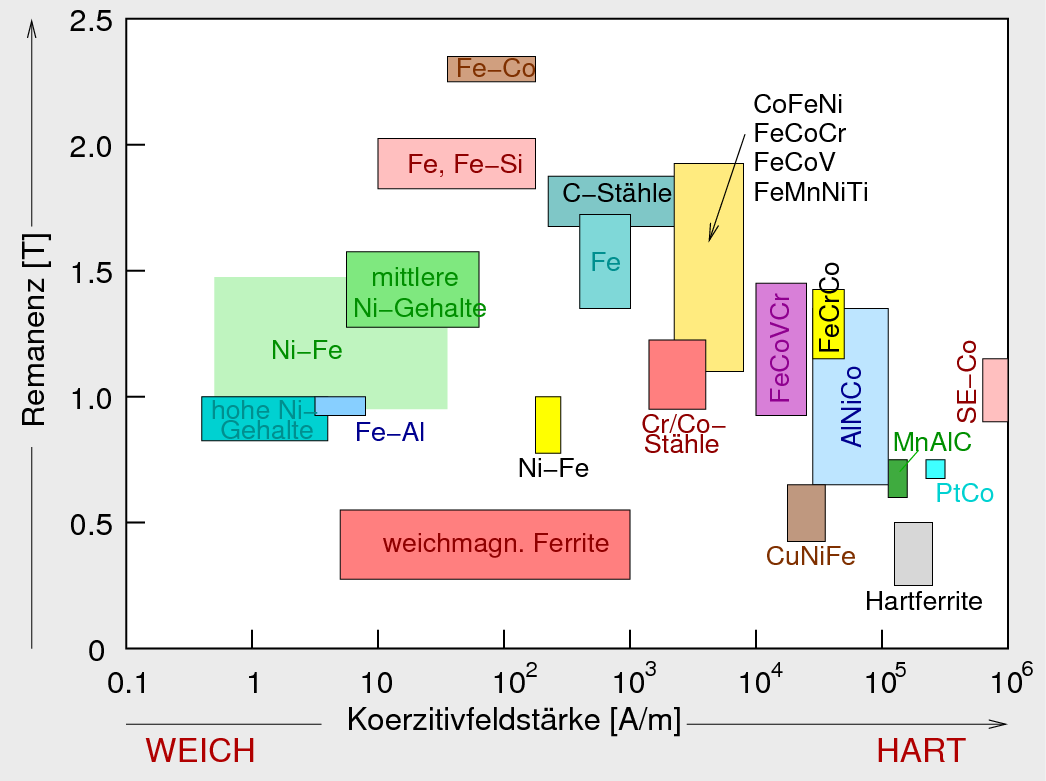
Einige komplizierte Legierungen (s. Exkurs bei den Laves-Phasen) sind als Magnetmaterialien noch deutlich besser geeignet als die reinen Elemente.
|
| Abb. 2.1.X. Übersicht Magnetmaterialien‣SVG |
Die thermische Ausdehnung beschreibt die Auswirkung von Temperaturänderungen auf das Volumen
oder die Länge (linearer thermischer Ausdehnungkoeffizient) des Materials:
| linearer thermischer Ausdehnungs- Koeffizienten [K-1 10 -6] | Wärmeleitfähigkeits- Koeffizient [W/mK] | |
| W | 4.5 | 178 |
| Cu | 16.5 | 398 |
| Ag | 19 | 428 |
| Al | 23.6 | 247 |
| Ge | 5.75 | 58.66 |
| Glas | 0.5 | 2 |
| Tab. 2.1.2. Thermische Eigenschaften einiger Metalle |
Die Tabelle 2.1.2. zeigt, dass alpha bei Metallen groß im Vergleich mit Nichtmetallen recht groß ist und
W einen vergleichsweise kleinen Ausdehnungskoeffizienten aufweist:
Bei Metallen besteht ein Zusammenhang zwischen elektrischer Leitfähigkeit und Wärmeleitung,
da für beide Transportprozesse nur die Elektronen verantwortlich sind: (sog. Wiedemann-Franz-Gesetz)
| JQ = | dQ | = | dU |
| ⎻⎻⎻ | ⎻⎻⎻ | ||
| dt | dz |
| Eg | Ladungsträger- Konzentration [e-/cm3] | e--Beweglichkeit [cm2/Vs] | spzifische Leitfähigkeit [Ω1- m-1] | Tc [K] für Supraleiter | |
| Si | 1.17 (i) | 1350 | 4 10-4 | ||
| Ge | 0.744 (i) | 3600 | 2.2 10-4 | ||
| Te | 0.33 (d) | 3600 | 2.2 10-4 | ||
| As | 0 | 2 1020 | |||
| Sb | 0 | 5.5 1019 | 2.8 | ||
| Bi | 0 | 2.88 1017 | 1 | ||
| K | 0 | 1.4 1022 | 15.9 106 | ||
| Na | 0 | 2.65 1022 | 23 106 | ||
| Cu | 0 | 9.3 1022 | 65 106 | ||
| Al | 0 | 38 106 | |||
| Hg | 4.4 106 | 4.2 |
| Tab. 2.1.2. Thermische Eigenschaften einiger Metalle |
Daneben sind thermoelektrische Eigenschaften von Metallen und Halbleitern technisch wichtig. Beispielsweise weist Bi2Te3 (Eg = 0.15 eV) eine thermoelektrische Kraft von 212 muV/K auf. Auch vom Peltier-Effekt verschiedener Metallkontakte wird technisch Gebrauch gemacht (z.B. bei Thermoelementen).
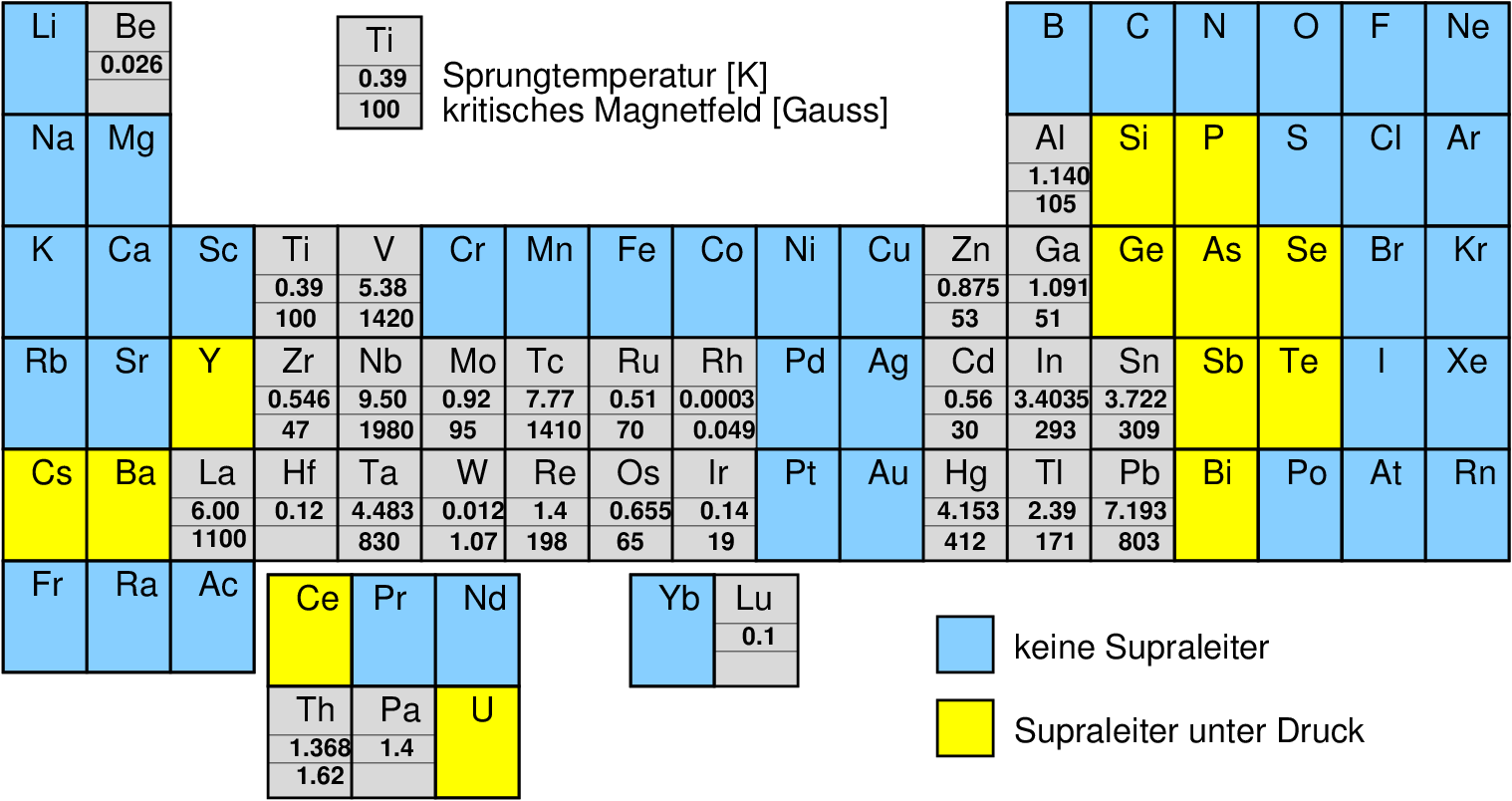
Einige wenige Elemente (s. Abb. 2.1.3.) sind bei sehr tiefen Temperaturen Supraleiter. Einige Legierungen (z.B. Nb3Sn) zeigen deutlich höhere Sprungtemperaturen und werden daher technisch in großem Umfang eingesetzt.
|
| Abb. 2.1.3. Supraleitung bei den Elementen‣SVG |
| ⇦ | Inhalt | Kap. 1 | Kap. 2 | Kap. 3 | Kap. 4 | Kap. 5 | Kap. 6 | Kap. 7 | Kap. 8 | Lit. | ⇨ |
| cr_home | Metalle | Nichtmetalle | Strukturchemie | Festkörperchemie | Oxide | Silicate | Strukturtypen |