2.2 Elektronische Strukturen

Die Stabilität bestimmter Strukturen der Metalle und die Bildung intermetallischer Phasen läßt sich nur durch die Betrachtung der elektronischen Zustände im Festkörper verstehen. Die Berechnung der elektronischen Verhältnisse ist zu komplex, um an dieser Stelle angesprochen zu werden. Es sollen nur kurz einige Plausibilitätsüberlegungen angestellt werden. Wichtig ist vor allem die Kenntnis der verschiedenen Arten der Darstellung elektronischer Strukturen. Welche Informationen über die Bindung und die physikalischen Eigenschaften lassen sich hieraus ersehen? Im Vergleich mit der kovalenten Bindung sind die sog. Bandstrukturen das Äquivalent zur MO-Darstellungen der Elektronenzustände und die Zustandsdichten das Äquivalent zu einfachen MO-Diagrammen (Zahl der Zustände im Energiebereich).
Für die erste Betrachtung der Elektronenzustände in Metallen reicht der einfachste und bekannte Fall der quantenmechanischen Behandlung, das Elektronen im eindimensionalen potentialfreien Kasten der Länge L, aus. Das Eigenwertproblem der Energie läßt sich in diesem Fall auf die kinetische Energie der Elektronen beschränken:
(Η - E) ψ(x) = 0 Für den Operator Η der kinetischen Energie gilt mit p = mv und E = ¹/₂ mv² daß:
E=^p²/_2m. (p²/2m - E) ψ(x) = 0 mit dem Impulsoperator p= ℏ \frac{\δ}{\δ x} folgt:
(\frac{ℏ²}{2m}\frac{\δ²}{\δx²} - E)ψ(x) = 0 d.h. E=1/2 m v² oder im Impuls ausgedrückt: E = p²/2m.
Als Lösungen des Eigenwertproblems erhält man einen Satz von Energieeigenfunktionen mit den zugehörigen Energieeigenwerten. Die Eigenwerte E sind proportional zum Quadrat der Quantenzahl n (Quantenzahl n, 'Kastenlänge' L):
E= (h²n²) / (8 m L²) mit der Einführung der von L unabhängigen Größe: k= 2π/L n folgt für die Eigenenergien:
E= h²k²/2m Die zugehörigen Eigenfunktionen sind einfache Wellenfunktionen:
ψ(x) = e^ikx = sin(kx) + i cos(kx) Die folgende Abbildung zeigt die graphische Darstellung dieser Ergebnisse:

Auf der linken Seite sind die Eigenfunktionen - stehende Welle im Kasten - für unterschiedliche Quantenzahlen n (= Zahl der Bäuche) dargestellt. Der direkter Vergleich mit der allgemeinen Wellengleichung
k = \frac{ 2 π}{λ}x zeigt, daß die Quantenzahl k:

die Einheit einer reziproken Länge besitzt.
k propotional ist zum Impuls der Elektronen (p=ℏk)
k als eindimensionaler Vektor einen reziproken Raum aufspannt (hier eine reziproke Linie)
k ist proportional 1/λ, wenn λ die Wellenlänge der stehenden Welle ist (sog. Blochwelle)

Rechts sind die Eigenwerte dargestellt. Da die Zahl der Elektronen im Kristall sehr hoch ist, liegen die entsprechenden Zustände sehr dicht. Die Auftragung von E gegen k nennt man Bandstruktur. E ist im Fall freier Elektronen im Kasten proportional zu k². Interessant ist für die chemische Bindung, wie viele Energieniveaus in einem Intervall dE liegen. Die entsprechende Auftragung nennt man Zustandsdicht. Gelegentlich wird die Energie auch nach oben dargestellt, so daß die von MO-Theorie bekannt Darstellung resultiert. Die Auffüllung der Elektronen auf die vorhandenen Zustände unter Beachtung des Pauliprinzip liefert zudem den Zustand maximaler Energie, die sogenannte Fermienergie E_F. Der dazugehörige Bereich im k-Raum heißt Fermipunkt (im 3-dimensionalen Fall Fermifläche).

Die erste Näherung der potentialfreien Kiste muß für die Erklärung der Strukturen und Bindungsverhältnisse in Metallen um das positive Potential der Kerne erweitert werden. Die Lösungen des Energieeigenwertproblems weiche im eindimensionalen Fall unter dem Einfluß des periodischen Potentials der Kerne immer dann von den Lösungen für freie Eleketronen ab, wenn λ in der Nähe der Gitterabstände ist, d.h. wenn k = π/a ist:

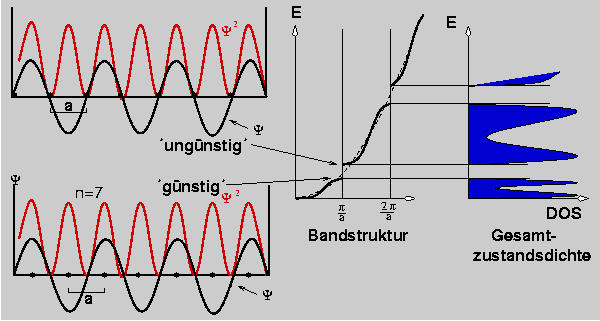Für λ=2a (mit k=2π/λ folgt k=π/a) ergeben sich bereits anschaulich 'günstige' Lösungen (unten), bei denen das Quadrat der Wellenfunktion, d.h. die Aufenthaltswahrscheinlichkeit der Elektronen an den Kernorten maximal ist (Coulomb-Wechselwirkungen maximal, Kompensation der Kernladung durch die Elektronen) und 'ungünstige' Funktionen (oben), bei denen die Maxima zwischen den Atomrümpfen zu liegen kommen. In der Bandstruktur (Abb. Mitte) ist die potentialfreie Parabel gestrichelt eingezeichnt. bei k=π/a ergibt sich bei gleichem λ eine Bandlücke, d.h. ein Energielücke in den zu besetztenden Zuständen, die sich selbstverständlich dann auch in der DOS-Kurve entsprechend wiederfindet.
Für die Darstellung der Bandstruktur im k-Raum werden verschiedene Möglichkeiten verwendet:

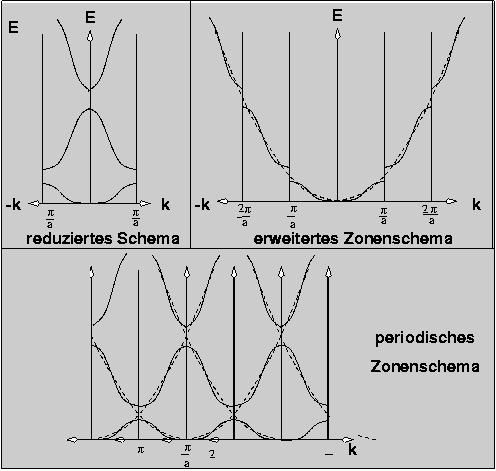Das erweitertes Zonenschema (oben rechts) entspricht den oben abgeleiteten Darstellungen. Bei der meist verwendeten Darstellung im reduzierten Schema (oben links) werden die Bänder auf die kleinste Einheit (Elementarzelle) des reziproken Gitters (die sogenannte 1. Brillouinzone = Wigner-Seitz-Zelle) 'eingefaltet', d.h. so lange an den eingezeichneten Geraden bei nπ/a gespiegelt, bis die Bänder in der 1. BZ liegen. (von k=0 (Γ-Punkt) bis π/a). Für die Erklärung der physikalischen Eigenschaften der Elektronen ist die dritte Möglichkeit, die Darstellung im periodischen Zonenschema, gebräuchlich (Abb. unten). Dieses kann aus dem reduzierten Schema durch Einführung von Translationssymmetrie (Aneinandersetzten!) erhalten werden (s. auch unten).
Im Folgenden werden die Betrachtungen nun auf den 2-dimensionalen Fall erweitert. Als Beipiel ist in der Abbildung unten eine einfache quadratische Anordnung von Kernen gezeigt:

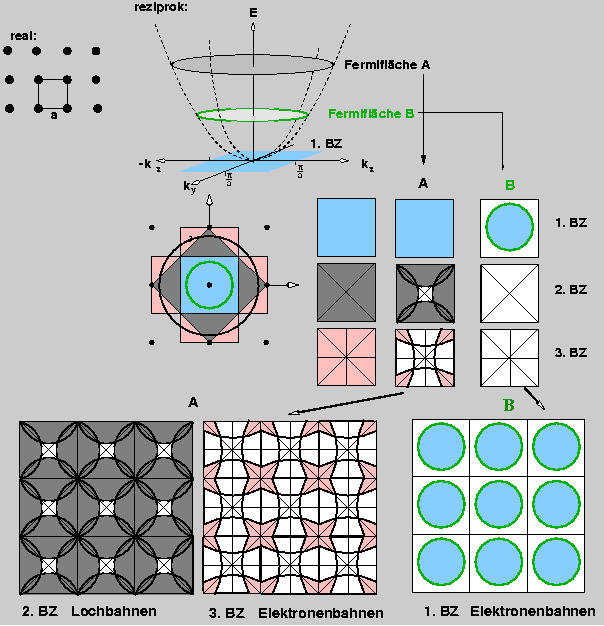Die Lösungen der Eigenwertproblem enthalten nun zwei Quantenzahlen mit zwei Indizes (k_x und k_y), die eine reziproke Ebene aufspannen. k_x,y sind Vektoren auf einer reziproken Fläche. Die Darstellung analog zum eindimensionalen Fall (ohne Berücksichtigung der Kernpotentiale!) zeigt als Bandstruktur den Rotationskörper der Parabel. Der Fermipunkt wird zu einer Fermilinie (Ring). Oben ist die 1. Brillouin-Zone (die Elementarzelle des reziproken k-Raums) hellblau eingezeichnet. (Konstruktion der Brillouin-Zonen: Ausgehend von k=0 Verbindungslinien zu den nächsten (1. BZ) Nachbarpunkten einzeichen. Die auf halber Länge dieser Linien senkrecht stehenden Geraden (Flächen) sind die Kanten (Flächen) der 1. Brilloiun-Zone. 2. BZ mit den 2.nächsten Nachbarn entsprechend usw.). In der Projektion (Mitte links) ist die 1. Brillouin-Zone hellblau, die 2. grau und die 3. rot eingezeichnet. Die Formen der reduzierten Zonendarstellung der Brillouinzonen (durch Spiegeln an den Zonengrenzen) sind rechts davon dargestellt. Die beiden Fälle A und B zeigen die Fermilinien bei unterschiedlicher Besetzung der Zustände mit Elektronen (d.h unterschiedlichen Fermiflächen im k-Raum). Mit wenigen Elektronen (z.B. 1 Elektron pro Atom) ist die 1. Brillouin-Zone nur partiell besetzt (Fall B). Werden mehr Elektronen (z.B. 3 pro Atom) eingefüllt, so sind die ersten drei Brilloinzonen besetzt (Fall A), die 1. voll, die zweite fast voll und die dritte nur zu einem geringen Anteil. Unten sind die entsprechenden Darstellungen im periodischen Zonenschema gezeichnet: Danach liegen bei B reine Elektronenbahnen, bei A Lochbahnen in der 2. Brillouin-Zone (fast volständig besetzt) und in Elektronenbahnen in der 3. BZ vor.
Zur vereinfachten graphische Darstellung der Bandstruktur werden die Bandverläufe nur entlang bestimmter Linien in der asymmetrischen Einheit des k-Raums (weiß) dargestellt:

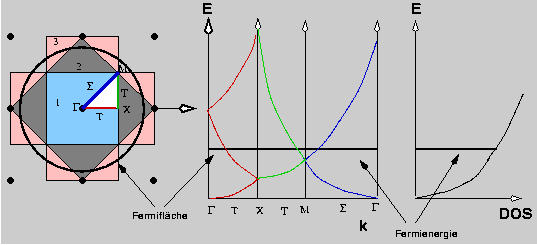Die speziellen Punkte (bestimmte Symmetrie) werden durch große (griechische) Buchstaben gekennzeichnet. Für den Fall A von oben ist zu erkennen:

rot (von Γ nach K) wie 1. dim. Kette
blau: ebenso, aber weiter raus
grün = Verbindung zwischen beiden

aber sichtbar: E_F 1. Band in allen Bereichen besetzt \\ d.h. Fermifläche überstreicht die assymmetrische Einheit \\
Im 3-dimensionalen Fall hat der k-Vektor drei Kompontenten (Vektoren im k-Raum mit Endpunkten $k_{x,y,z}). Die Darstellung der Energie gegen k würde 4 Dimesnionen erfordern. Gebräuchlich sind daher:

Darstellung der Fermiflächen:
- Kugeln entsprechen freien Elektronen
- real treten diverse andere Figuren auf
- Aus der Form rückschlüsse auf physikalische Eigenschaften
Darstellung von E gegen k entlang bestimmter Richtungen im reziproken k-Raum (s.o.).

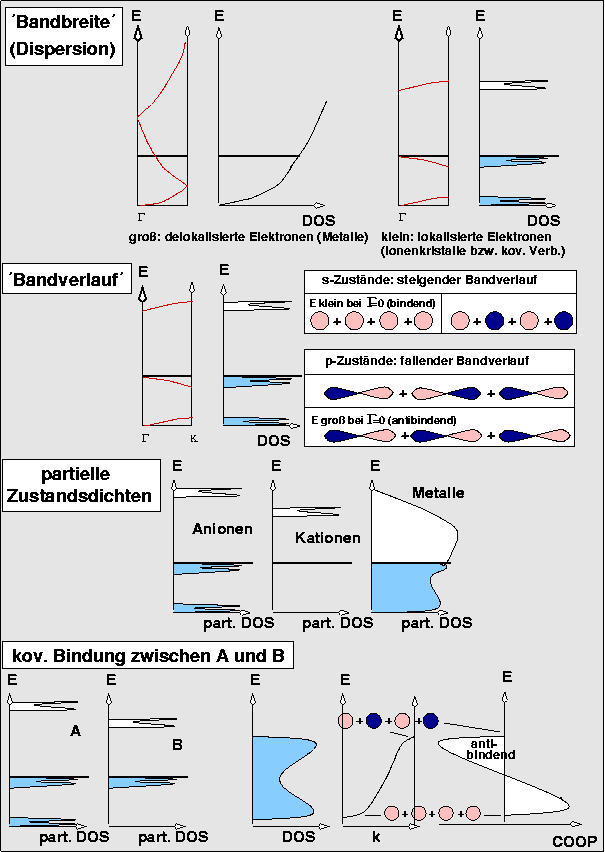
\fbox{Wo steckt die chem. Information in den Bandstrukturen} \\ \> \psfig{figure=./Xfig_bilder/band_6.ps,width=9.3cm,angle=-90.} \\ \> $\bullet$ 1. Bandbreite = Dispersion \\ \> - Potentialfrei = freies $e^-$-Gas = unendlich breite Bänder (Metall) \\ \> - wie schon gesehen, wenn + der Kerne Bandlücke, stark, wenn ψ₂ am Kern hoch \\ \> \> $\mapsto$ Ionenkristall oder kovalente Bindung \\ \\ \> $\bullet$ 2. Bandverlauf = Info über die Topologie der WW \\ \> \> (Vorsicht: setzt MO-Beschreibung vorraus \\ \> \> \> antibindend = steigende Bänder \\ \\ \> $\bullet$ 3. pertielle Zustandsdichten \\ \> \> Anionen (besetzt, scharf, unter $E_F$ \\ \> \> Kationen (alles unbesetzt, scharf, über $E_f$ \\ \> \> Metall (breit, partielle besetzt \\ \ \> $\bullet$ 4. kovalente Bindungen:\\ \> - aus partiellen DOS: Zustände mit gleicher Energie \\ \> - aus Hückel oder FP-Methoden: COOP-Plots (Crystal Orbital Overlapp-Population) \\ \> \> bindende und antibindende Teile eines Bandes\\ \

⇦

Inhalt

Kap. 1

Kap. 2

Kap. 3

Kap. 4

Kap. 5

Kap. 6

Kap. 7

Kap. 8

Lit.

⇨

Oxide