Vorlesung Strukturchemie der Oxide

4. Nichtstöchiometrische binäre Oxide

Verbindungen, die im Übergangsbereich zwischen stöchiometrischen und nichtstöchiometrischen Bereich liegen, sind die bereits seit mehr als 50 Jahren bekannten sogenannte reduzierte W- und Mo-Oxide, in denen einige der M⁶⁺-Ionen zu M⁵⁺ reduziert ist. Die Darstellung dieser Verbindungen erfolgt durch Reduktion von WO₃ bzw. MoO₃ entweder durch die Umsetzung der Trioxide MO₃ mit metallischem M oder durch schwaches Glühen von MO₃ im Wasserstoff-Strom. Umsetzungen dieser Art liefern ein Vielzahl intensiv gefärbter Phasen. Thermodynamische Untersuchungen zeigen, dass zwischen MO₃ und M₂O₃ ( = MO_2.5) Phasen mit Phasenbreite existieren. Für Wolfram sind sie in der folgenden Tabelle 4.1. zusammengestellt:

Verbindung	x	Farbe
α-WO_x	3.00 - 2.98	zitronengelb
β-WO_x	2.90 - 2.83	blauviolett
γ-WO_x	2.72 - 2.66	rotviolett
δ-WO_x	2.00 (Rutil)	braun

Tab. 4.1. Wolfram-Oxide
Obwohl diese Verbindungen zunächst nach echter Nichtstöchiometrie aussehen, konnte Magneli ca. 1950 (daher der Name Magneli-Phasen) die Strukturen stöchiometrisch zusammengesetzte Verbindungen bestimmen:

Verbindung	x	Name
W₄₀O₁₁₉	WO_2.975	α-WO_x
W₅₀O₁₄₈	WO_2.96	Grenze zu α
W₂₀O₅₈	WO_2.90	β-WO_x
W₁₈O₄₉	WO_2.72	γ-WO_x

Tab. 4.2. Stöchiometrische Wolfram-Oxide
Ein sehr ähnliches Bild ergibt sich für die Mo-Oxide, wie die folgende Tabelle 4.3. zeigt.

Phasen	x	Struktur
α-MoO_x	3.00 - 2.95	Schichtstruktur
β-MoO_x	2.75 - 2.65
γ-MoO_x	2.00 - 1.97	Rutil

Tab. 4.3. Stöchiometrische Molybdän-Oxide
Hier sind die Strukturen stöchiometrischer Phasen zwischen der α- und der β-Phase bekannt (Tab. 4.4.).

Verbindung	x
Mo₉O₂₆	MoO_2.89
Mo₈O₂₃	MoO_2.875
Mo₁₇O₄₇	MoO_2.76

Tab. 4.4. Stöchiometrische Molybdän-Oxide zwischen der α- und der β-Phase
Dazu gibt es etliche gemischte Mo-W-Oxide mit komplizierten Zusammensetzungen.
Alle Zusammensetzungen und Strukturen lassen sich als Scherstrukturen von ReO₃ erklären. In allen Oxiden liegt M in oktaedrischer Koordination vor. Die Zahl der gemeinsamen Kanten zwischen den MO₆-Oktaedern kann einen weiten Bereich der Zusammensetzung erklären und reicht von TiO (( NaCl-Typ, acht gemeinsame Kanten) über TiO₂ (Anatas, vier gemeinsame Kanten) und V₂O₅ (zwei gemeinsame Kanten) schließlich bis zum ReO₃ (keine gemeinsamen Kanten). Die W-, Mo- und Nb-Oxide liegen zwischen den beiden letzten Zusammensetzungen M₂O₅ und MO₃. Entsprechend lassen sich ausgehend von ReO₃ durch Einführung sogenannter kristallographischer Scherungen entlang bestimmter Richtungen und in bestimmnten Abständen (diese führt zu mehr Kantenverknüpfung = abnehmendem O-Gehalt = mehr M⁵⁺) die Strukturen und Zusammensetzung dieser Phasen erklären:

Die Tabelle 4.5. zeigt zunächst Beispiele für Scherungen in nur eine Richtung hk0.

	Scherung	Richtung (hk0)	Formel	Beispiel
A		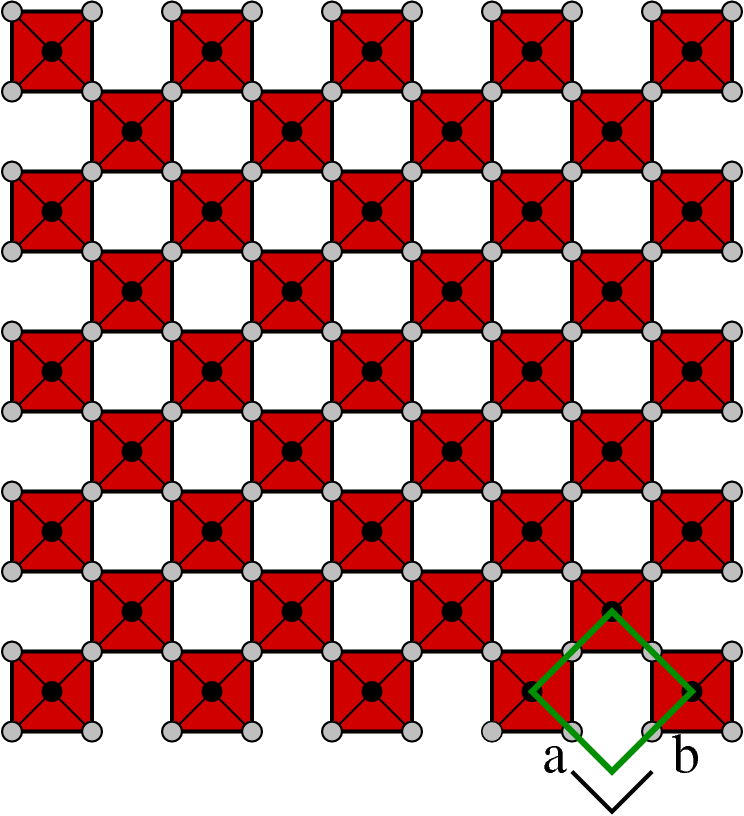(000)	MO₃	ReO₃
B		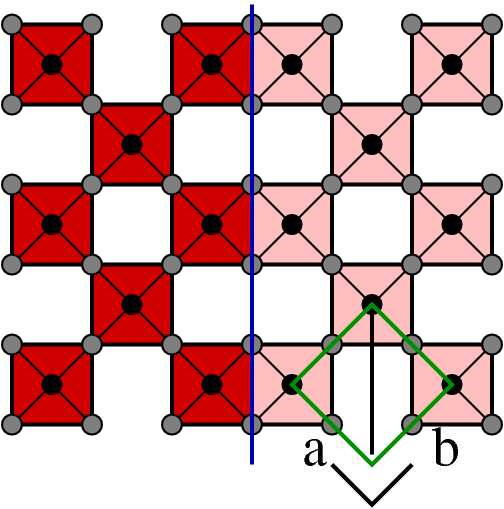(110)	MO₃	keine
C		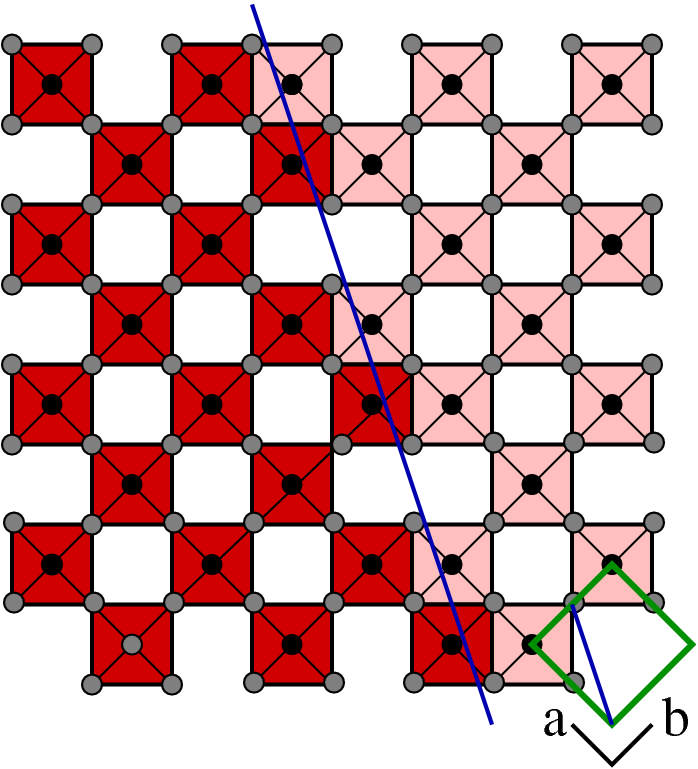(120)	M_nO_3n-1	Mo₈O₂₃
D		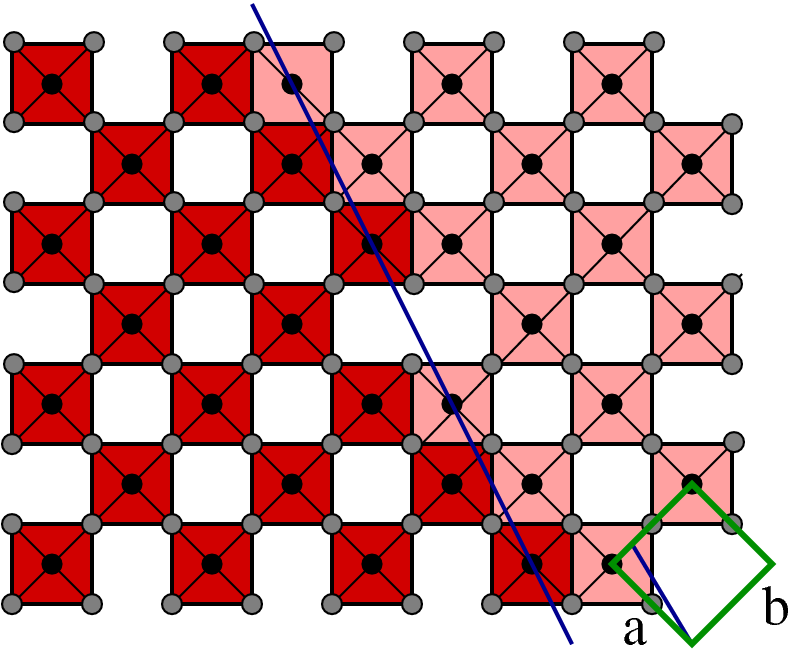(130)	M_nO_3n-2	W₂₀O₅₈, W₅₀O₁₄₈
E		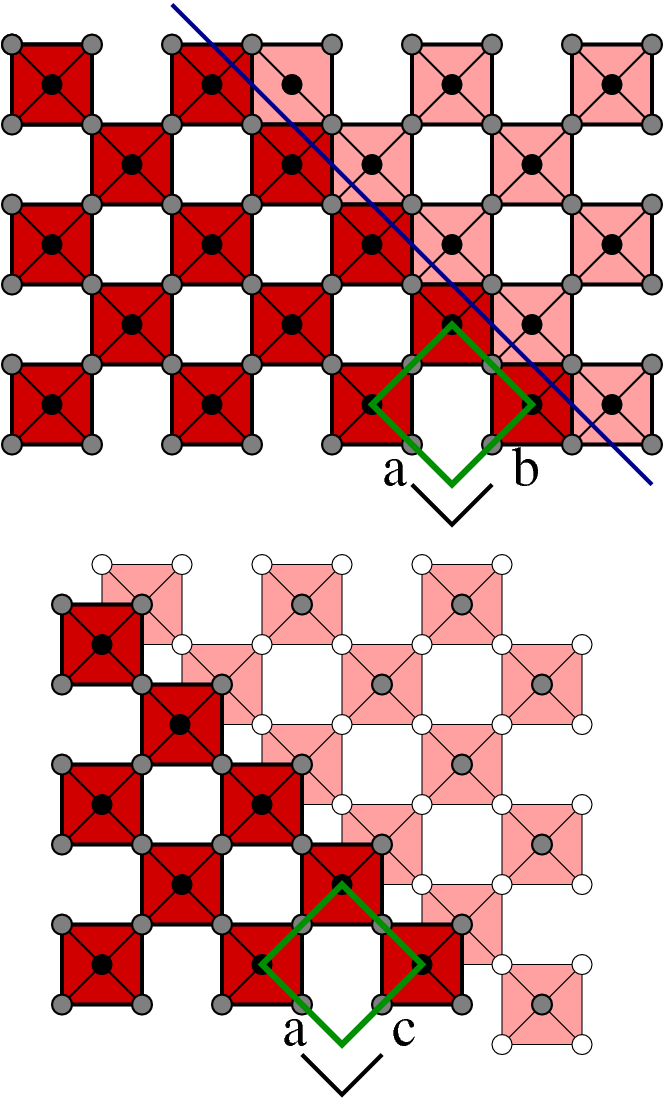(010)	M_mO_3m-1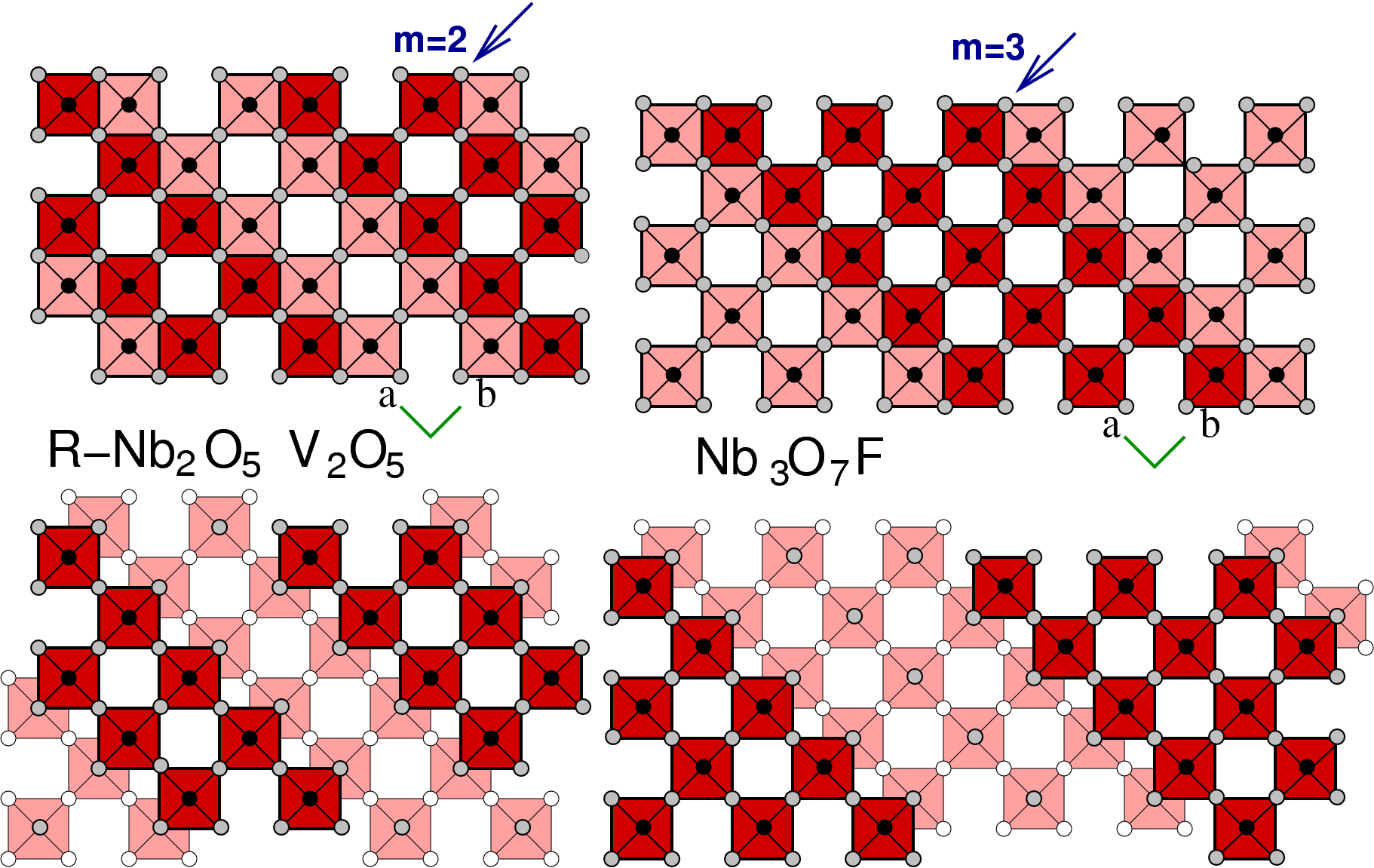

Tab. 4.5. Scherstrukturen von ReO₃ mit Scherungen in eine Richtung hk0
Im Einzelnen zu Tabelle 4.5.:

A: Die Basis für alle weiteren Strukturen ist der ReO₃-Typ, hier als Projektion auf eine der kubischen Achsen. Nach oben und unten liegt weitere Eckverknüpfung der Oktaeder vor.
B: Die einfachste mögliche Scherung verläuft über die Flächendiagonale der Elementarzelle der ReO₃-Struktur, die Richtung (1 1 0). Beispiele für diese Scherungen kommen NICHT vor! Die Stöchiometrie würde MO₃ bleiben.
C: Durch Scherung entlang (1 2 0) entstehen entlang der Scherrichtung MO₆-Oktaeder mit zwei und einer gemeinsamen Kante. Die Stöchiometrie dieser Serie ist M_nO_3n-1 oder ganz allgemein bei Vorgabe der Scherrichtung M_nO_3n-(k-l). Hierbei ist n die Zahl der eckverknüpften Oktaeder in (1 0 0). Beispiel: Mo₈O₂₃; Weitere Vertreter dieser Serie: sind Mo₉O₂₆ und W₄₀O₁₁₉ und die ganze Serie (W,Mo)_nO_3n-1 mit n=8,9,10,11,12,14 und wechselndem W/Mo-Verhältnis.
D: Scherung entlang (1 3 0) ergibt wieder die Zusammensetzungen M_nO_3n-(k-h) = M_nO_3n-2. Einzige Vertreter sind hier W₅₀O₁₄₈ und W₂₀O₅₈.
E: Die weitere Fortsetzung dieser Art der Scherung führt schließlich auf (1 k 0) mit k gegen ∞, d.h. auf die Richtung (0 1 0). Dadurch ergibt sich eine neue Serie von Scherstrukturen, die vor allem bei V- und Nb-Oxiden auftritt. Die allgemeine Formel für diese Phasen ist M_mO_3m-1 wobei jetzt m die Zahl der eckverknüpften Oktaeder in (0 1 0) bezeichnet. Beispiele sind (m = 2) V₂O₅, R-Nb₂O₅ und (m = 3) Nb₃O₇F.

Eine ganze Serie weiterer Oxide läßt sich durch zwei solcher Scherung, die senkrecht zueinander verlaufen, erklären (sog. Block- oder besser Säulenstrukturen). Der einfachste Fall ist jeweils eine Scherung in (1 0 0) und eine in (0 1 0), so dass Säulen aus ReO₃-Einheiten bestehen bleiben. An den Blockgrenzen findet sich auch Kantenverknüpfung von Okatedern.
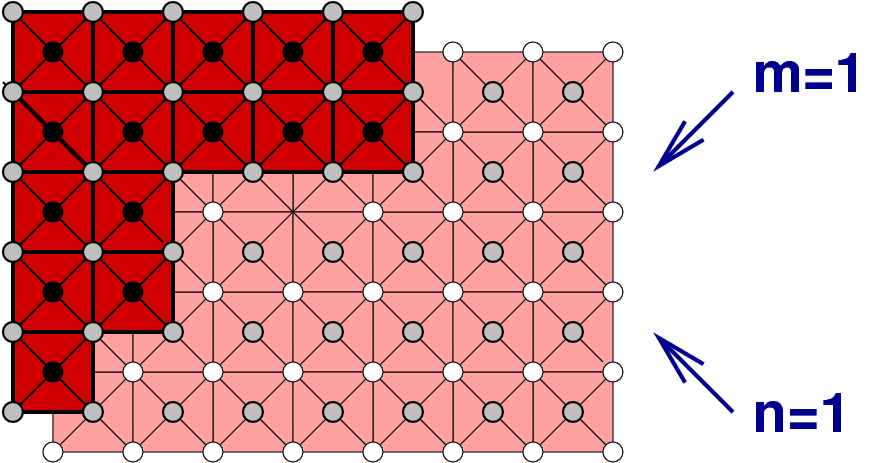
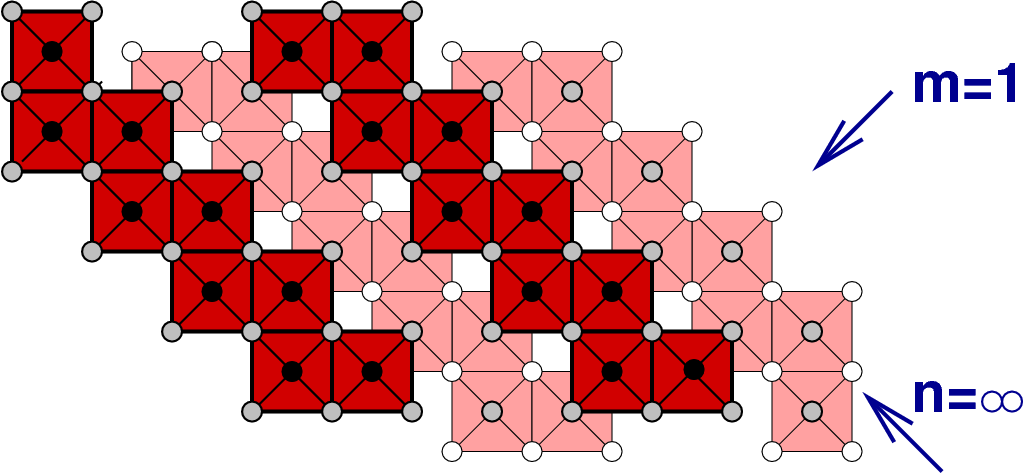
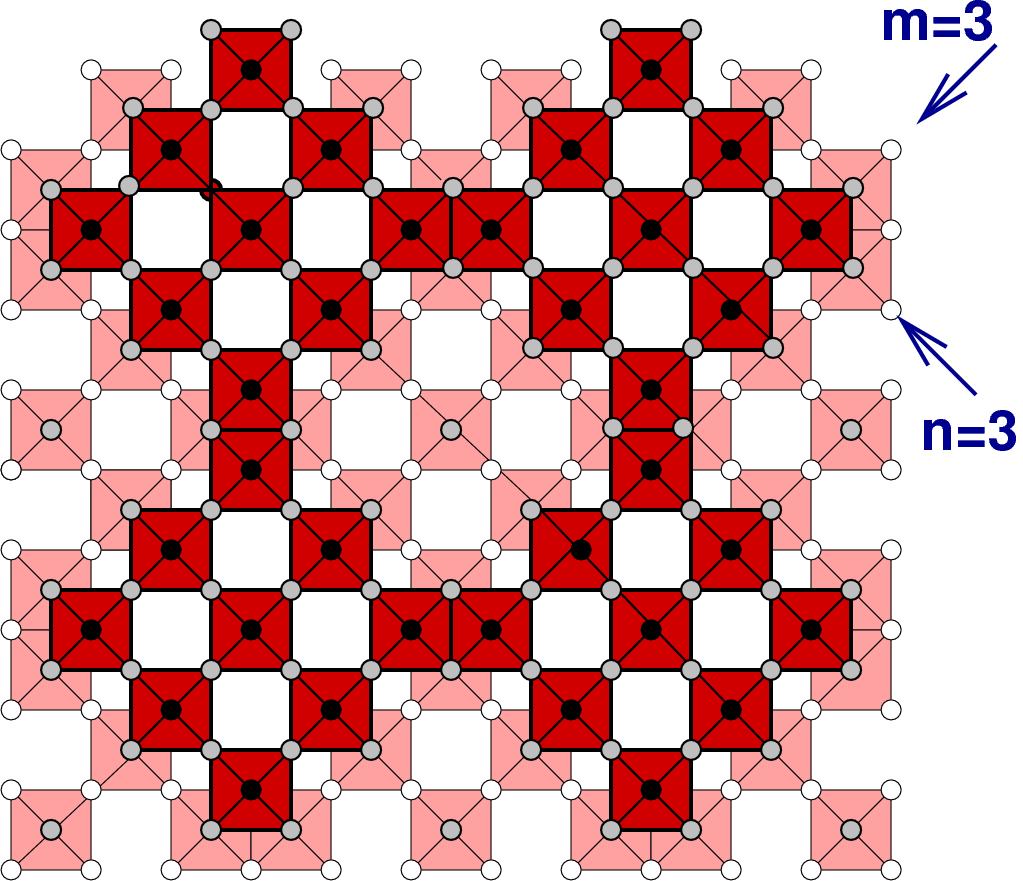
In die allgemeine Formel

M_mnO_3mn-(m+n) geht die Zahl der eckverknüpften Oktaeder in (1 0 0) (n) und (0 1 0) (m) ein, d.h. die sogenannte Blockgröße. Die einzelnen Beispiele sind in Tabelle 4.6. zusammengestellt.

x in MO_x	Blockgrösse	Stöchiometrie	Beispiele
2.33	3 x 3	M₉O₂₁ = M₃O₇	TiNb₂O₇, TiTa₂O₇
2.417	3 x 4	M₁₂O_36-7 = M₁₂O₂₉	Nb₁₂O₂₉, Ti₂Nb₁₀O₁₉
2.5	4 x 4	M₁₆O_3*16-8 = M₁₆O₄₀ = M₂O₅	M-Nb₂O₅
2.5	∞ x 2	M_{2 ∞}O_{6 ∞ -(∞ + 2)} = M₂O₅	R-Nb₂O₅, V₂O₅
2.67	∞ x 3	M_{3 ∞} O _{9 ∞ - (∞ + 3)} = M₃O₈	Nb₃O₇F
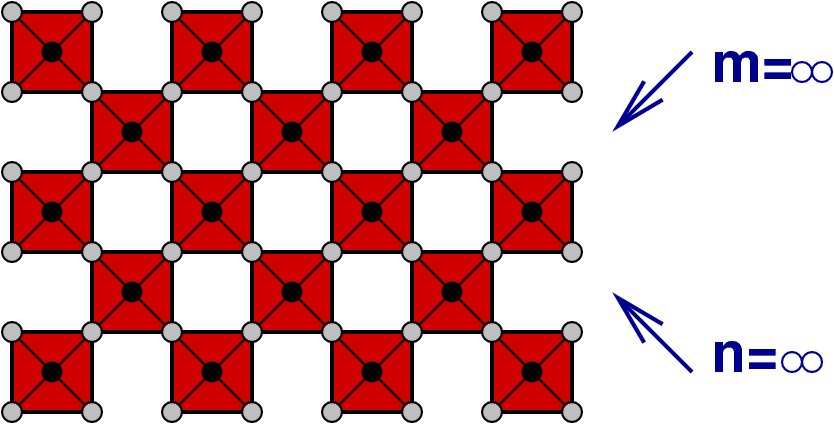
3	∞ x ∞	M_{∞ ∞}O_{3 ∞ ∞-(∞+2)} = MO₃	ReO₃

Tab. 4.6. Scherstrukturen von ReO₃ mit Scherungen in die beiden Richtungen (100) und (010)

Die folgende tabellarische Übersicht (Tab. 4.7.) zeigt, dass diese Phasen zwischen NaCl (alle Kanten gemeinsam, Strukturtyp) und ReO₃ (keine gemeinsame Kanten) liegt.

x	n	m	allgemeine Formel	Beispiele	Abbildung
1	1	1	MO	TiO (NaCl-Typ)
2	∞	1	MO₂	TiO₂ (Anatas)
2.33	3	3	M₉O₂₁ = M₃O₇	TiNb₂O₇
2.417	3	4	M₁₂O₂₉	Nb₁₂O₂₉
2.5	4	4	M₂O₅	M-Nb₂O₅
2.5	∞	2	M₂O₅	R-Nb₂O₅
2.67	∞	3	M₃O₈	Nb₃O₇F
3	∞	∞	MO₃	ReO₃

Tab. 4.7. Scherstrukturen von ReO₃ mit Scherungen in die beiden Richtungen (100) und (010)

Diese Formel geht in die für die eindimensionale Scherung der gleichen Art über, wenn ein Index unendlich gesetzt wird. Wenn die Blöcke in beide Richtungen ∞-groß sind, muß letztlich wieder der ReO₃-Typ resultieren.

Neben diesen einfachen Blockstrukturen gibt es noch eine riesige Zahl weiterer Scherstrukturen, bei denen die Blöcke in komplizierterer Weise verknüpft sind und andere allgemeine Formeln resultieren. Weitere Variationen entstehen durch Einbau von Elementen in die Tetraederlücken, die dann bevorzugt die Blockecken besetzen (z.B. PNb₉O₂₅).

Echte Nichtstöchiometrie kommt bei Verbindungen dieser Art zustande, wenn nicht-periodische Scherungen vorliegen.

Die Strukturaufklärung solcher Phasen ist röntgenographisch äußerst kompliziert, da der überwiegende Teil der Struktur ReO₃ entspricht und für die eigentliche Strukturbestimmung die sehr schwachen Überstrukturreflexe ausgewertet werden müssen. Heute werden die Strukturen solcher Phasen mit großem Erfolg mit Hilfe von hochauflösender Elektronenmikroskopie aufgeklärt.

Im letzten Kapitel folgt nach den vielen komplizierten Stöchiometrien eine Betrachtung der Strukturchemie ternärer Oxide mit einer gleichbleibenden Zusammensetzung.

<< SEITE ZURÜCK Inhalt Kap. 1 Kap. 2 Kap. 3 Kap. 4 Kap. 5 SEITE WEITER >>