Vorlesung Anorganische Strukturchemie
3. Strukturchemie von Metallen und Legierungen
3.1. Bindung, Konzepte, Radien
Das Prinzip der Bindung in Metallen und Legierugen ist die Überlappung der
elektronischen Zuständen zu breiten Bändern, wobei es zu einer Überlappung
möglichst vieler Zustände kommt. Energiegewinn ist dann wie bei den Molekülen
die Absenkung der Elektronenenergien. Die Folge dieses Bindungskonzeptes sind, dass
- ungerichtete
- langreichweitige (über ganzen Kristall gehende)
Wechselwirkungen auftreten. Die strukturchemischen Folgen sind
hohe Koordinationszahlen von 8 bis 24 (Motto: gleiche Bindungspartner, möglichst viele
möglichst nahe Nachbarn).
Die Überlappung der elektronischen Zustände der Einzelatome wird in der
breiten Zustandsdichte (Density of States, DOS) deutlich. Die Darstellung der DOS entspricht
etwa dem MO-Schema bei kovalenten Verbindungen. Hauptprinzip für die Strukturchemie
sind maximale Packungsdichte, sofern echte Metalle mit kleiner Elektronegativität
vorliegen. Die Valenzelektronenkonzentration (VEC: Zahl der Valenzelektronen pro Atom)
ist für die Besetzung der Zustände und damit häufig auch für den auftretenden
Strukturtyp wichtig. Zur chemischen Bindung in Metallen und Legierungen, inklusive
einem Vergleich mit dem kovalenten LCAO-Ansatz, gibt es wieder ein
PDF: Bandstrukturen II: NFE/Tight-Binding/PW-Konzept.
Für die Verbindungsbildung sind (nicht nur im Fall der Metalle) im wesentlichen drei
Größen wichtig:
- Die Valenzelektronenkonzentration (kurz VEC)
ist die Zahl der Elektronen/Atom. Diese Größe ist z.B. das
entscheidende Kriterium für die Frage der möglichen Verbindungen
- bei kovalenten Verbindungen (8-N-Regel)
- bei Ionenkristallen (Edelgasschale für Ionen => VEC=4)
Die VEC ist auch bei intermetallischen Phasen oft sehr wichtig.
Das Problem bei der Betrachtung der VEC ist die Zahl der Valenzelektronen, die
zwar für viele Metalle (z.B. Na=1, Mg=2, Al=3) unmittelbar klar ist,
die bei vielen anderen Metallen aber auch vom Bindungspartner
abhängen kann. Besonders heikel sind die 3d-Metalle, bei denen die
Beteiligung der d-Orbitale in den Metallen und Legierungen sehr stark schwankt.
- Radien (metallische Radien!) sind ein sehr kompliziertes Problem.
Sie hängen nicht nur von der Valenz, sondern auch von der Koordinationszahl
ab.
- Die Elektronegativität. Diese sollte bei Metallen und Legierungen
klein sein, ansonsten gibt es Übergänge zu anderen Bindungsarten (s. z.B. die Zintl-Phasen).
Die Tabelle 3.1.1. enthält die Werte für die Elektronegativitäten nach Pauling
und die metallische Radien für die Koordinationszahl (CN) 12 für die angegebenen Valenzen
(nach Teatum, Gschneidner, Waber).
| | Li | Be | |
| EN | 1.0 | 1.5 |
| rMetall | 156 | 113 |
| Valenz | 1 | 2 |
|
| | Na | Mg | | Al | Si | |
| EN | 0.9 | 1.2 | 1.5 | 1.8 |
| rMetall | 191 | 160 | 143 | 132 |
| Valenz | 1 | 2 | 3 | 4 |
|
| | K | Ca | Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | Ga | Ge | As | Se |
| EN | 0.8 | 1.0 | 1.3 | 1.5 | 1.6 | 1.6 | 1.5 | 1.8 | 1.8 | 1.8 | 1.9 | 1.6 | 1.6 | 1.8 | 2.0 | 2.4 |
| rMetall | 238 | 197 | 164 | 146 | 135 | 128 | 126 | 127 | 125 | 125 | 128 | 139 | 141 | 137 | 139 | 140 |
| Valenz | 1 | 2 | 3 | 4 | 5 | 6 | 6 | 6 | 6 | 6 | 1 | 2 | 3 | 4 | 5 | 6 |
|
| | Rb | Sr | Y | Zr | Nb | Mo | Tc | Ru | Rh | Pd | Ag | Cd | In | Sn | Sb | Te |
| EN | 0.8 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 1.9 | 2.2 | 2.2 | 2.2 | 1.9 | 1.7 | 1.7 | 1.8 | 1.9 | 2.1 |
| rMetall | 255 | 215 | 180 | 160 | 147 | 140 | 136 | 134 | 135 | 138 | 145 | 157 | 166 | 155 | 159 | 160 |
| Valenz | 1 | 2 | 3 | 4 | 5 | 6 | 6 | 6 | 6 | 6 | 1 | 2 | 3 | 4 | 5 | 6 |
|
| | Cs | Ba | La | Hf | Ta | W | Re | Os | Ir | Pt | Au | Hg | Tl | Pb | Bi | Po |
| EN | 0.7 | 0.9 | 1.1 | 1.3 | 1.5 | 1.7 | 1.9 | 2.2 | 2.2 | 2.2 | 2.4 | 1.9 | 1.8 | 1.8 | 1.9 | 2.0 |
| rMetall | 273 | 224 | 188 | 158 | 147 | 141 | 138 | 135 | 136 | 139 | 144 | 157 | 172 | 175 | 170 | 176 |
| Valenz | 1 | 2 | 3 | 4 | 5 | 6 | 6 | 6 | 6 | 6 | 1 | 2 | 3 | 4 | 5 | 6 |
Tab. 3.1.1. Elektronegativitäten, Radien und Valenzelektronenzahlen von Metallen
Gemäß der allgemeinen Tendenzen innerhalb der Periodensystems nimmt die Elektronegativität von oben nach unten leicht ab, nach rechts
nimmt sie zu. Die metallischen Radien nehmen nach unten zu und durchlaufen von links nach rechts ein Minimum in der Co- und Ni-Gruppe.
Entsprechend dieser Größen lassen sich die Metalle und damit dann die Gruppen intermetallischer Phasen abgrenzen.
Obwohl eine klare Trennung verschiedener Gruppen intermetallischer Phasen
nicht einfach möglich ist, lassen sich doch eine Reihe von Verbindungstypen
abgrenzen, wenn man die Kombinationen bestimmter Gruppen von Metallen
betrachtet:
Die Metalle der A-Gruppen werden als echte Metalle bezeichnet. Zu diesen Gruppen
gehören alle Metalle im Periodensystem (von links) bis zur Cu-Gruppe.
Die B-Elemente sind Metalle/Halbleiter mit zunehmend kovalenten Bindungsanteilen, die z.T.
mit besonderen Strukturen und in weniger dichten Packungen kristallisieren.
Diese beiden Gruppen lassen sich nochmals weiter unterteilen:
- A1: elektropositive Metalle (Alkali- und Erdalkali-Metalle) mit z.T. sehr großen Metallradien
- A2: Übergangsmetalle (außer Zn, Cd, Hg), die vergleichbare Metallradien und gleiche Elektronegativitäten
aufweisen, sich aber in der Zahl der Valenzelektronen unterscheiden.
- B1: Elemente der Zn-Gruppe, Elemente der III.-Hauptgruppe, (Sn) und
Pb. Diese Metalle sind stärker elektronegativ und kristallisieren meist in besonderen,
jedoch noch nicht in echten kovalenten, Strukturen. Es treten noch keine Bandlücken auf,
gelegentlich deuten sich Pseudobandlücken an (s. z.B. Abb. 3.2.6. für Gallium).
Aluminium und Blei sind die einzigen beiden B1-Elemente, die eine gewöhnliche
Metallstruktur (f.c.c.) ausbilden.
- B2: Si, Ge, (Sn), Elemente der V. und VI.-Hauptgruppe,
die sich strukturell auf der
Basis kovalenter Wechselwirkung (8-N-Regel, Grimm-Sommerfeld-Verbindungen) verstehen
lassen und den Übergang zu den Nichtmetallen bilden. Es liegen bereits geringe Bandlücken vor
bzw. die Zustandsdichte am Ferminiveau verschwindet.
Zusammenfassend ist die Verteilung der Gruppen im Periodensystem in Tabelle 3.1.2. dargestellt.
| H |
| | | | | | | |
| | | | | | | |
He |
| Li |
Be |
| | | | | | | |
| |
B |
C |
N |
O |
F |
Ne |
| Na |
Mg |
| | | | | | | |
| |
Al |
Si |
P |
S |
Cl |
Ar |
| K |
Ca |
Sc |
Ti |
V |
Cr |
Mn |
Fe |
Co |
Ni |
Cu |
Zn |
Ga |
Ge |
As |
Se |
Br |
Kr |
| Rb |
Sr |
Y |
Zr |
Nb |
Mo |
Tc |
Ru |
Rh |
Pd |
Ag |
Cd |
In |
Sn |
Sb |
Te |
I |
Xe |
| Cs |
Ba |
La |
Hf |
Ta |
W |
Re |
Os |
Ir |
Pt |
Au |
Hg |
Tl |
Pb |
Bi |
Po |
At |
Rn |
Tab. 3.1.2. Gruppen metallischer Elemente
Entsprechend dieser Einteilung der Metalle lassen sich die
binären intermetallischen Phasen als Kombinationen der Gruppen
befriedigend klassifizieren (die angegebenen Beispielsysteme sind
durch die Phasendiagramme (als Bilder) belegt):
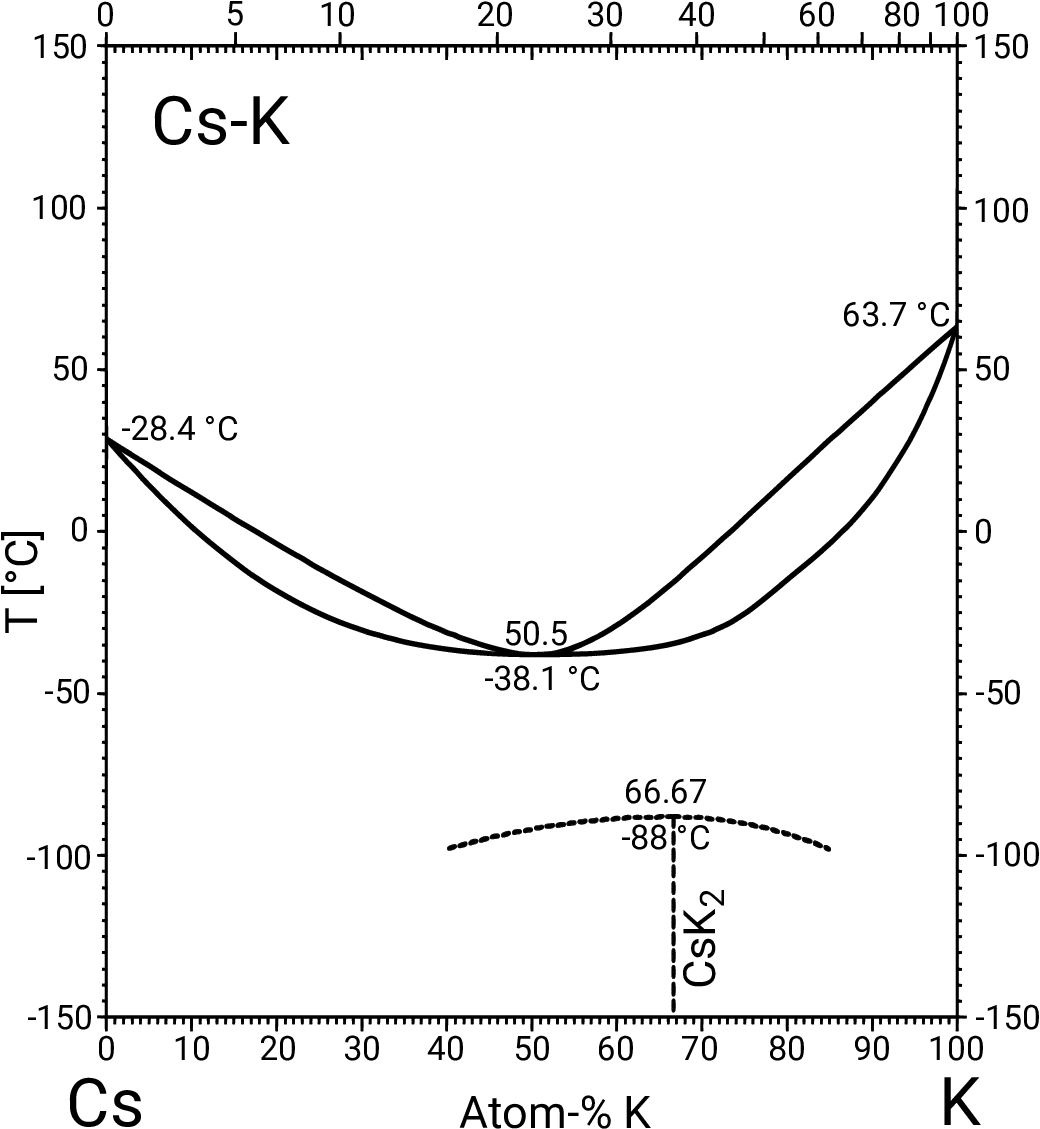
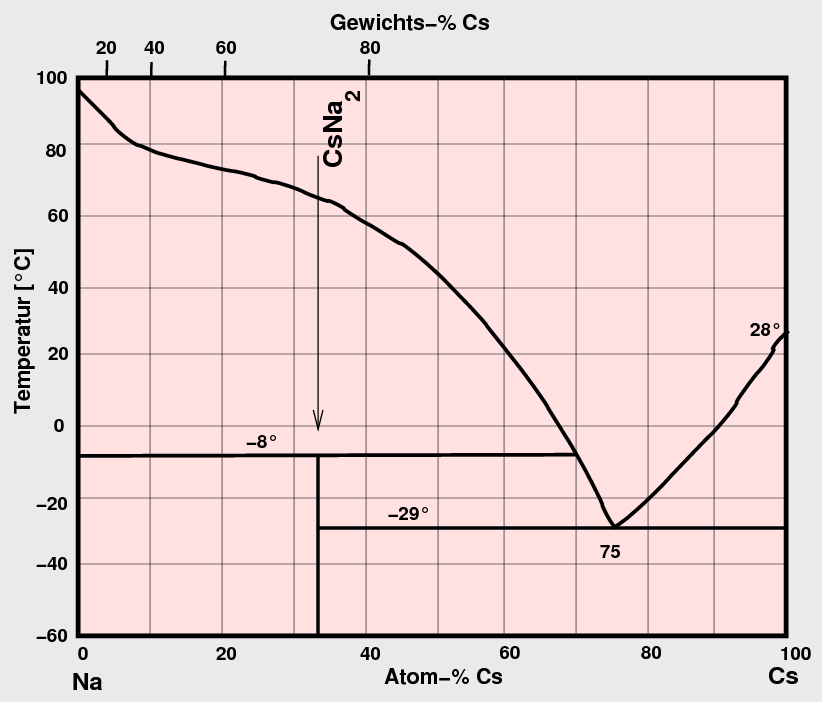
- A1-A1: Bei gleicher Valenzelektronenzahl und vergleichbaren Metallradien tritt vollständige Löslichkeit
auf (z.B. Rb-Cs, Abb. 3.1.3. links).
Bei unterschiedlichen Metallradien oder unterschiedlichen VE-Zahlen bilden sich definierte Verbindungen,
oft packungsdominierte Laves-Phasen-Phasen bzw. verwandte Verbindungen
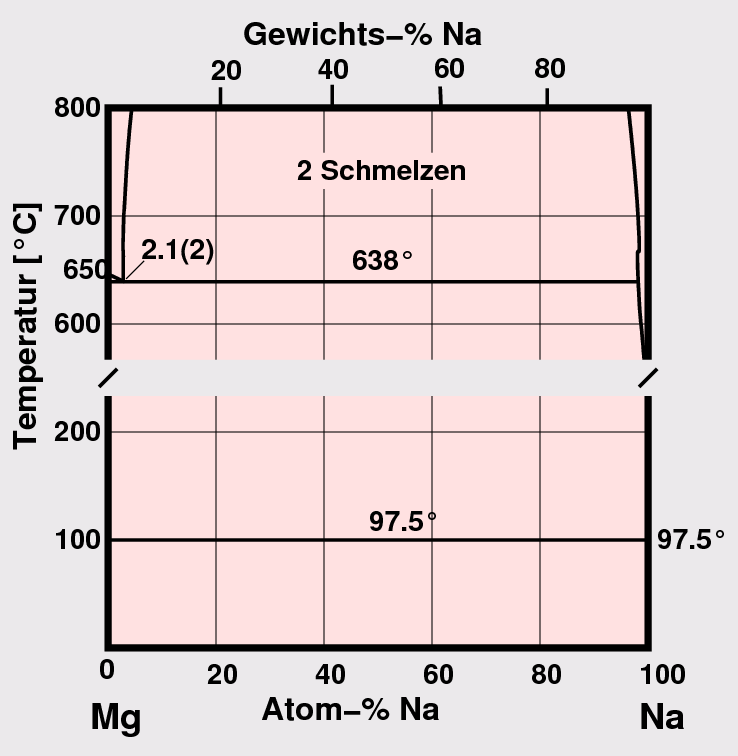
(z.B. Na-Cs, Abb. 3.1.3. Mitte). Bei starken Unterschieden in Radien oder in der
Valenzelektronenzahl kann auch vollständige Entmischung der
beiden Metalle auftreten (z.B. Na-Mg in Abb. 3.1.3. rechts). Li- und Mg-Systeme bilden auch Verbindungen mit Phasenbreiten.
Abb. 3.1.3. Beispiele für Phasendiagramme der A1-A1-Kombination
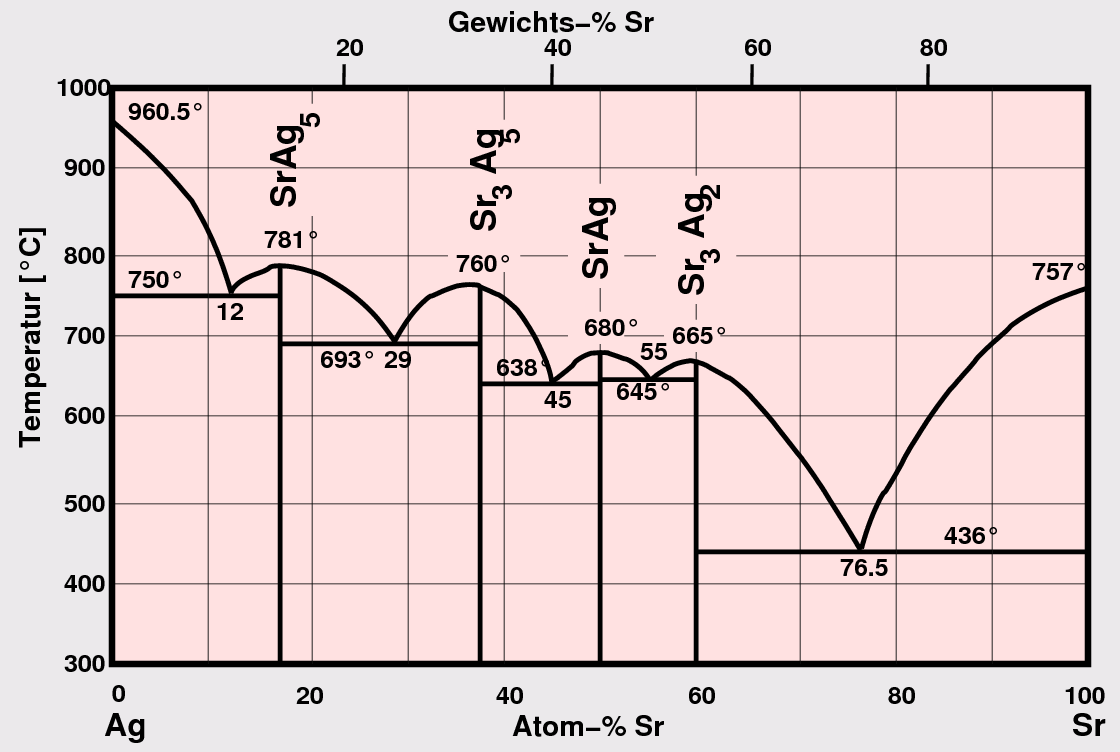
- A1-A2: In diesen Systemen sind
Laves-Phasen und Verwandte sehr häufig
(s. z.B. Sr-Ag in Abb. 3.1.4.). Oft tritt auch überhaupt keine Verbindungsbildung auf.
Abb. 3.1.4. Phasendiagramm einer A1-A2-Kombination
- A1-B1 Verbindungen an der
Zintl-Grenze, Laves-Phasen-Phasen.
In dieser Gruppe überwiegen stöchiometrisch scharfe
Verbindungen. Da Δ r meist groß und die Elektronegativitätsdifferenz ebenfalls groß ist.
Es gibt viele besondere Strukturen, aber auch einige häufigere wie z.B. die CsCl- und NaTl-Struktur.
Einige Phasen folgen als Clusterverbindungen den Wade-Regeln. Diese Systeme bilden den Übergang zu den
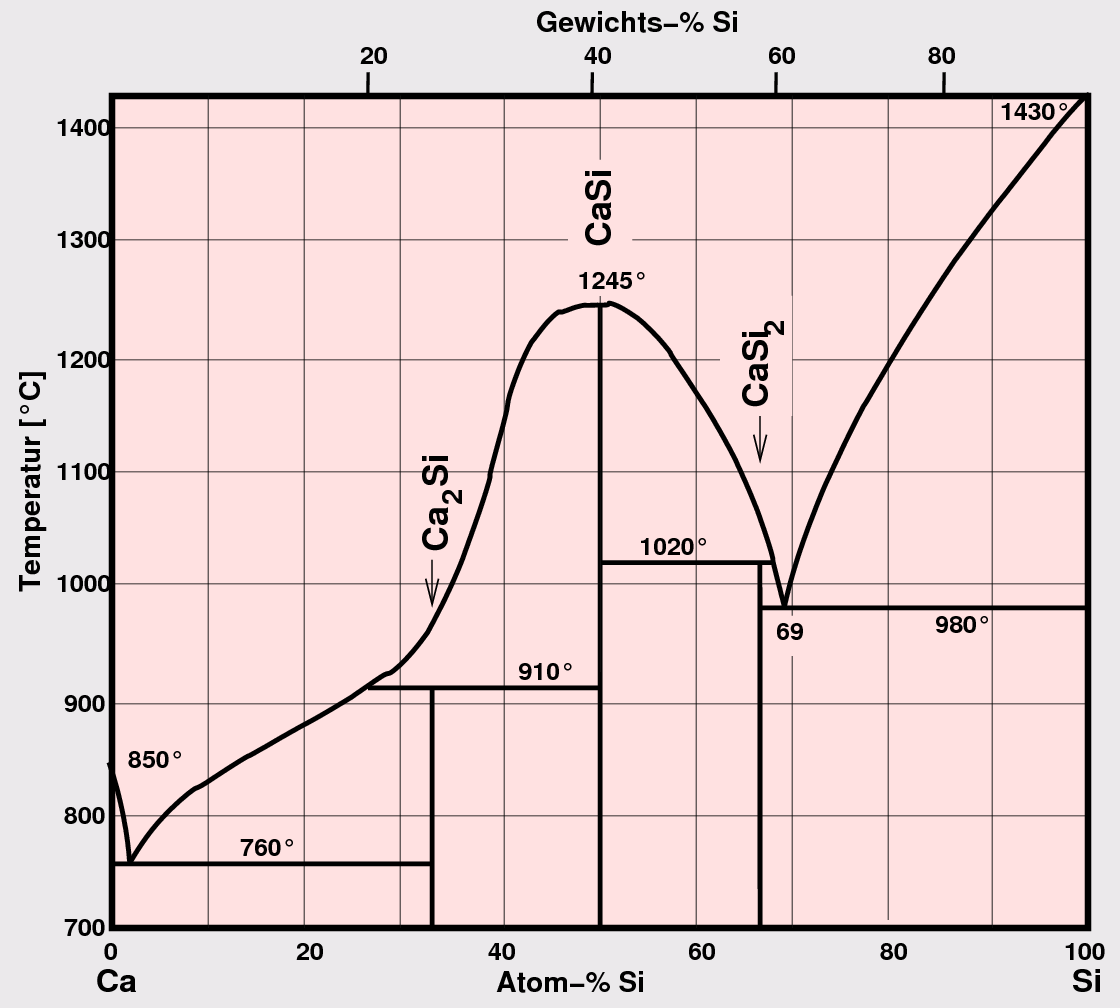
- A1-B2:
Zintl-Phasen. Alle Verbindungen dieser Kombination sind stöchiometrisch. Die Strukturchemie
ist sehr vielfältig, es greifen jedoch die Konzepte ionischer und kovalenter
Verbindungen zu deren Erklärung (s. das Phasendiagramm Ca-Si als Beispiel in Abb. 3.1.5.).
In der Vorlesung haben wir die Kristallchemie dieser Phasen im Kapitel 2.4. bei den Polyanionen besprochen.
Abb. 3.1.5. Phasendiagramm einer A1-B2-Kombination (Zintl-Phasen)
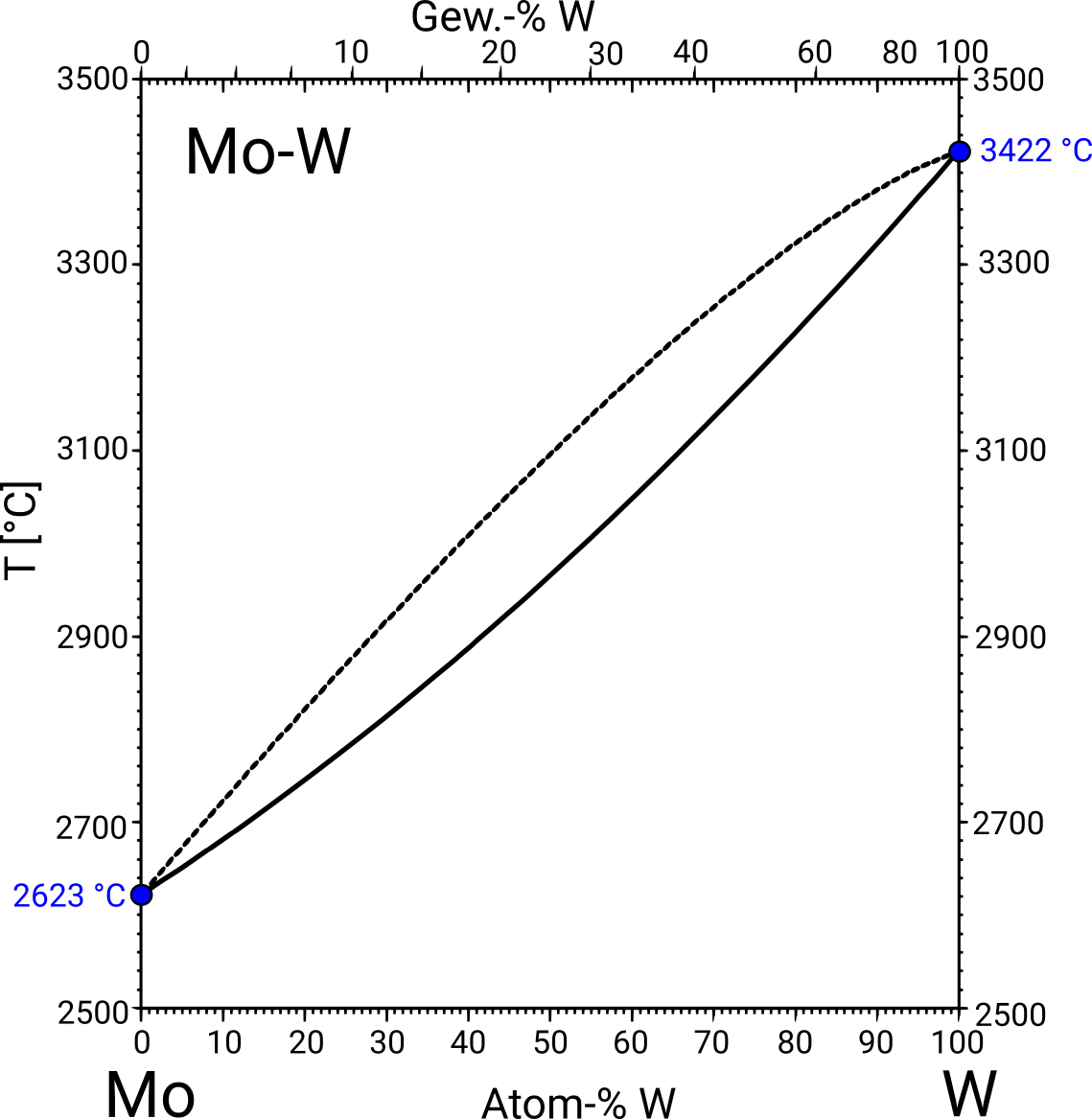
- A2-A2 i.A. liegen
feste Lösungen mit großen Phasenbreiten vor (z.B. Co-Pt).
Bei niedrigeren Temperaturen treten
Überstrukturen auf (z.B. Cu-Au, Abb. 3.1.6.).
Die Löslichkeit der beiden A2-Metalle ineinander ist im wesentlichen von der Radiendifferenz der beiden
Partner abhängig. Zu dieser Gruppe gehören fast alle technisch (Maschinenbau, Bau) wichtigen
Legierungen (z.B. Stähle).
Abb. 3.1.6. Phasendiagramm von A2-A2-Kombinationen
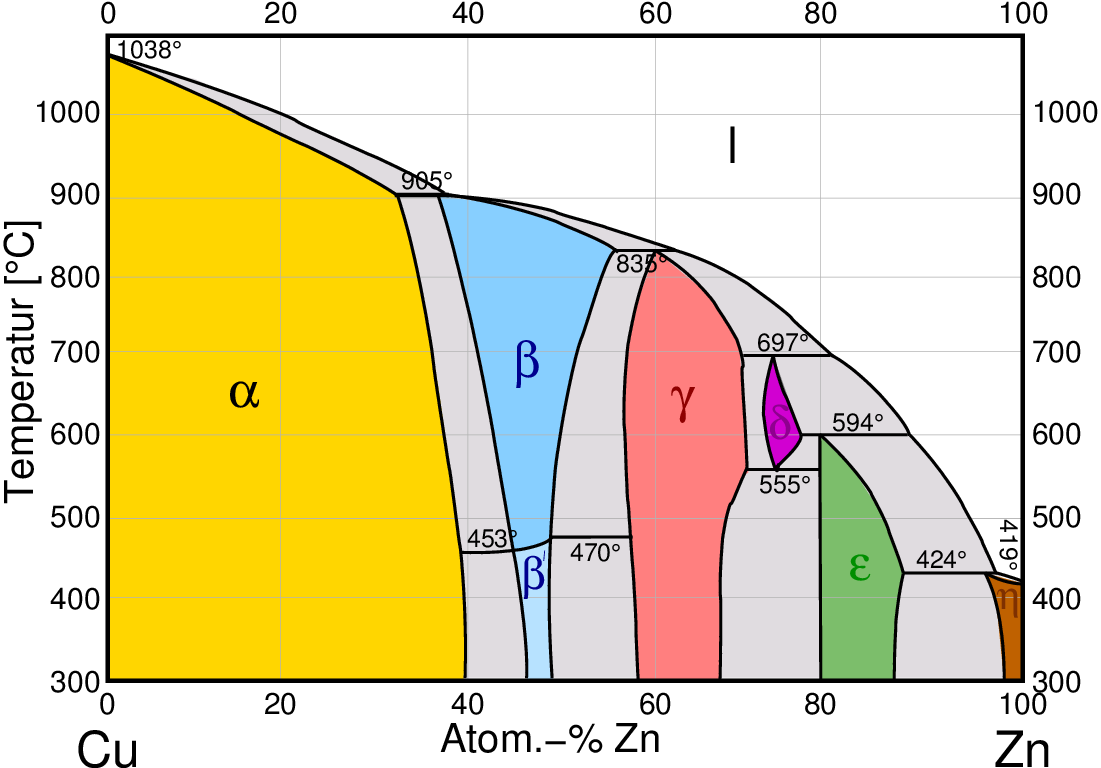
- A2-B1
Hume-Rothery-Phasen (Elektronenverbindungen) zeigen kleinere bis mittlere Phasenbreiten.
Die Strukturchemie ist fast ausschließlich von den elektronischen Verhältnissen (VEC) bestimmt.
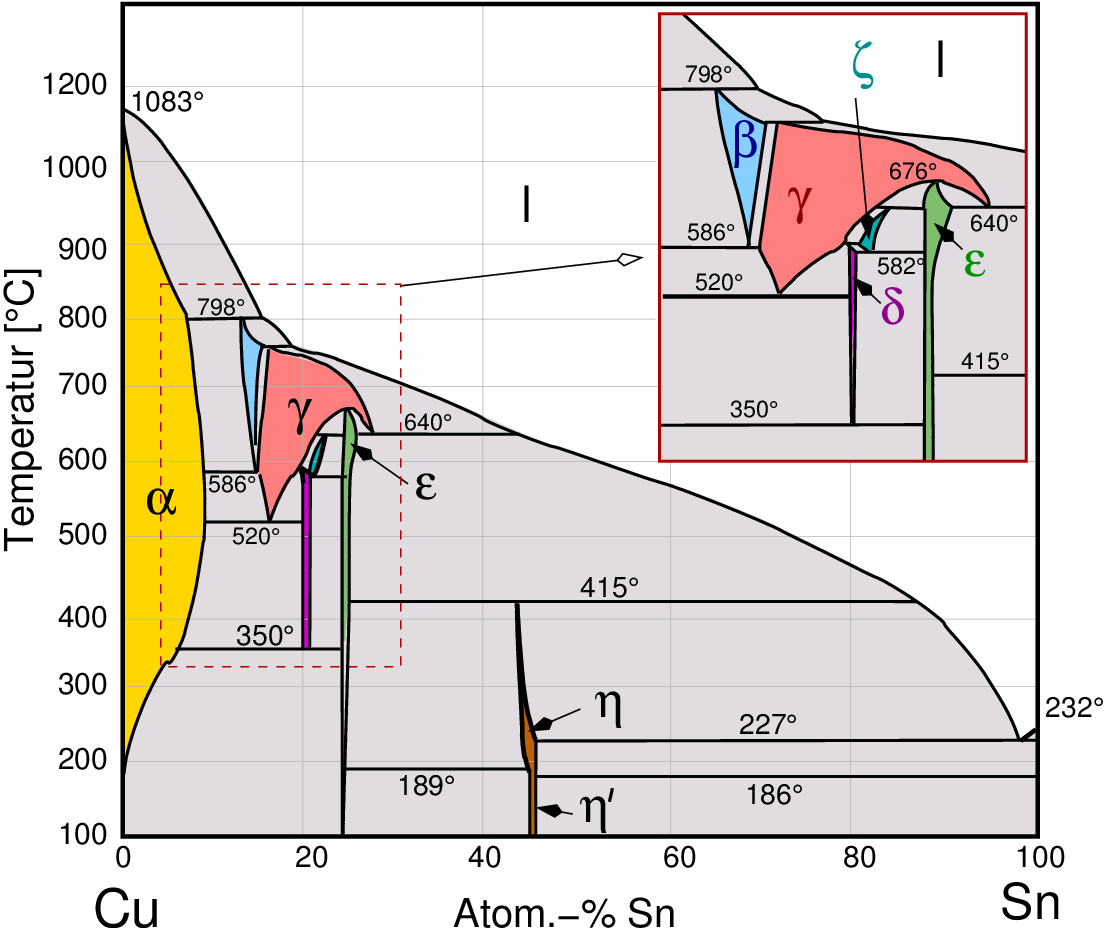
(s. Abb. 3.1.7. links das Beispiel das Phasendiagramm des Systems Cu-Zn
(Messing) und rechts das entsprechende Diagramm des Systems Cu-Sn (Bronze).
Abb. 3.1.7. Phasendiagramme von A2-B1-Kombinationen (Hume-Rothery-Phasen)
- A2-B2 Die Phasen dieser Systeme sind entweder stöchiometrisch, oder sie weisen kleinere Phasenbreiten auf.
(z.B. As-Co, As-Fe, As-Ni, Co-Si).
Häufig bildet die B2-Komponente eine dichteste Packung, in der die Lücken mit der A2-Komponente besetzt
werden können. Da Übergänge in der Lückenbesetzung möglich sind, gibt es z.T. auch Phasenbreiten.
In vielen Systemen existieren Verbindungen mit NiAs-Typ (h.c.p.-Packung, alle Oktaederlücken besetzt),
mit CdI2-Typ (h.c.p., 1/2 der Oktaederlücken besetzt (z.B. CoTe2, NiTe2)
oder mit Ni2Ge-Typ (h.c.p., oktaedrische und trigonale Lücken besetzt).
Ohne Übergänge und damit immer scharf sind die Verbindungen mit Markasit-, Pyrit-
oder MoS2-Struktur.
Auch diverse andere wichtige Strukturtypen gehören zu diesen Systemen (Cr3As; Cr3Si).
- B-B Bei den Systemen der
B-Metalle untereinander bilden sich oft feste Lösungen, wenn die
beiden Elemente derselben Gruppe angehören (z.B. Sb-Bi). Gehören sie zu unterschiedlichen Gruppen, so
kommen nur stöchiometrische Verbindungen vor, die deutlich kovalente Bindungsanteile aufweisen
(Grimm-Sommerfeld-Verbindungen).
Im der Tabelle 3.1.2. sind die Gruppen binärer intermetallischer Phasen nochmals
zusammengefaßt.
| A1 |
A2 |
B1 |
B2 |
| A1 |
Δr klein: vollständige Löslichkeit bei gleicher Valenzelektronenzahl;
Δr groß: Laves-Phasen u.ä. oder keine Verbindungsbildung
|
stöchiometrisch scharfe Verbindungen, unterschiedliche Strukturen, Laves-Phasen |
stöchiometrisch scharfe Verbindungen, Laves-Phasen, viele besondere Strukturen, CsCl- und NaTl-Typ, Clusterverbindungen,
Übergänge zu Zintl-Phasen |
Zintl-Phasen (vgl. Polyanionische Verbindungen) |
| A2 |
| da Δr klein: feste Lösungen, große Phasenbreiten, Überstrukturen und Ordnungsvarianten |
Hume-Rothery-Phasen (Elektronen-Verbindungen) |
NiAs-Varianten (CdI2 -> NiAs -> Ni2Ge (z.T. mit Phasenbreiten)); MoS2, Pyrit |
| B1 |
|
|
Elemente derselben Gruppe: feste Lösungen; Elemente unterschiedlicher Gruppen
meist stöchiometrisch scharfe Verbindungen |
| B2 |
|
|
|
mit stark kovalenten Bindungsanteilen |
Tab. 3.1.2. Intermetallische Systeme nach Kombination der Elementgruppen.
Diese Tabelle (Dreieck!) steht selbstverständlich direkt mit dem Ketelaar-Dreieck der Arten chemischer Bindung
in Bezug.
Bevor die binären Systeme im einzelnen besprochen werden, wird eine kurze Wiederholung zu
Strukturen (und Eigenschaften) der reinen
metallischen Elemente gegeben.