Vorlesung Chemie der Metalle
1. Einleitung, Allgemeines
1.3. Chemische Bindung in Metallen
Für die Art der chemische Bindung sind ganz generell wichtig:
- Summe der Elektronegativitäten der Bindungspartner (ΣEN)
- Differenz der Elektronegativitäten der Bindungspartner (ΔEN)
Danach lassen sich bekanntermaßen die drei Fälle chemischer Bindung unterschieden:
- ΣEN groß und Δ(EN) klein: kovalente Bindung,
Molekülverbindungen wie z.B. CO2, Cl2, HCN
oder Bor
- ΔEN groß: Salze, Ionenkristalle wie z.B. NaCl, CaO oder Al2O3
- ΣEN und ΔEN klein: Metalle und Legierungen
wie z.B. Cu oder Messing (Cu-Zn)
Da in Metallen und ihren Verbindungen keine großen Elektronegativitätssummen
auftreten können, spielen nur vor allem ionische und metallische Bindung eine Rolle. Nur in Komplexverbindungen
werden auch Modelle der kovalenten Bindung benötigt.
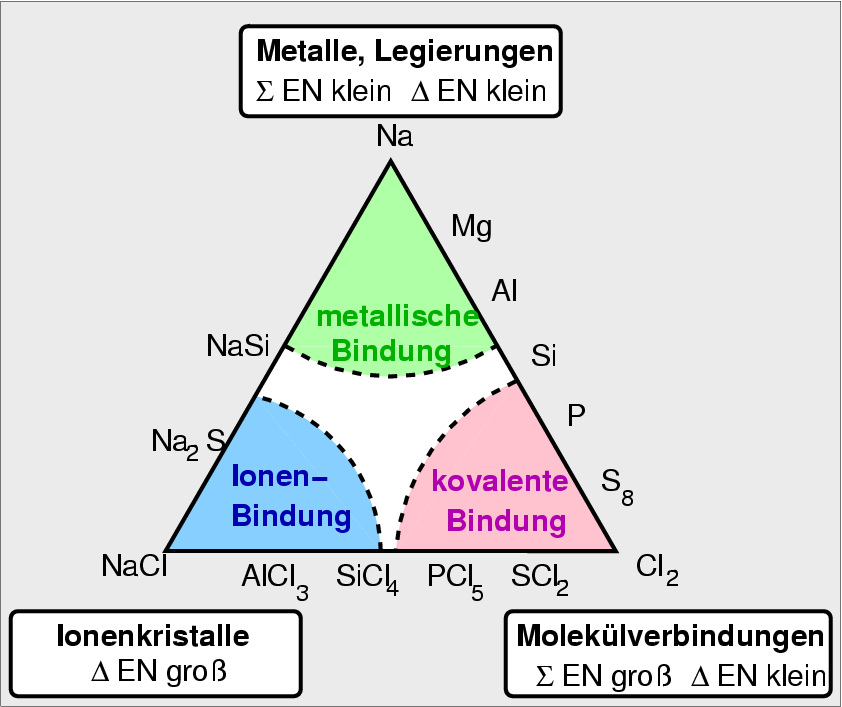
Das in Abbildung 1.3.1. dargestellte Dreieck (sog. Ketelaar-Dreieck) zeigt - mit Verbindungsbeispielen aus der 3. Periode - die
Bereiche und Übergänge zwischen den verschiedenen Bindungsarten.
Zur Erklärung der chemischen Bindung und der entsprechenden Strukturen und
Eigenschaften der Verbindungen werden verschiedene Konzepte benötigt:
- Kovalente Bindung liegt bei Verbindungen der Nichtmetallen untereinander vor.
- Das Prinzip kovalenter Bindungen ist das Teilen von Elektronen, so dass jeder Bindungspartner
eine 8er-Schale (Edelgasschale) erreicht. Beschreiben läßt sich
die Bindung durch die Bildung von Molekülorbitalen aus Atomorbitalen.
Die 'Bindungen' sind gerichtet.
- Die Strukturchemie bei kovalenten Verbindungen ist vielfältig (s. z.B. organische Verbindungen)
und komplex.
Da die maximale Koordinationszahl jedoch nur 4 ist, lassen sich die Strukturen der Verbindungen
graphisch leicht und übersichtlich darstellen. Es gibt
einfache Konzepte zur Erklärung der Strukturen, Eigenschaften und
Reaktivitäten wie z.B. das VSEPR-Konzept oder die 8-N-Regel.
- Die Eigenschaften der Stoffe hängen sehr wesentlich von der Dimensionalität der
Bauverbände ab.
- Zur Festkörperchemie kovalenter Verbindungen s. auch
Kap. 2. Strukturchemie kovalenter Verbindungen
aus der Vorlesung Anorganische Strukturchemie.
Dagegen sind für Metalle und ihre Verbindungen die beiden anderen Bindungsarten
wichtig:
- Die Ionenbindung kommt
durch Coulomb-Wechselwirkungen unterschiedlich geladener Ionen zustande, d.h.
die Kräfte sind ungerichtet.
Die Struktur von Salzen basieren auf einfachen Prinzipien:
Meist bildet die größeren Atomsorte (i.A. die Anionen) eine dichte Packung,
die kleinere Ionensorte besetzt die Lücken in dieser Packung.
Ziel der Packung ist ein maximaler Abstand gleich geladener Ionen und
ein minimaler Abstand unterschiedlich geladener Teilchen.
Die typischen Koordinationszahlen reichen von ca. 4 bis 8, so dass
die Strukturen i.A. relativ schwierig darstellbar sind.
Zur Strukturchemie von Ionenkristallen s. auch
Kap. 4. Strukturchemie von Ionenkristallen
aus der Vorlesung Anorganische Strukturchemie.
- Bei der metallischen Bindung
überlappen sehr viele elektronische Zustände.
Die Strukturchemie ist extrem einfach, es liegen ungerichtete Bindungen vor.
Prinzip ist die maximal dichte Packung aller Atome, wie die
Strukturen der Metalle (s. Kap. 1.4.) zeigen.
Da die Koordinationszahlen mit 8 bis 24 sehr hoch sind, machen allerdings
graphische Darstellungen größere Schwierigkeiten.
Zur Strukturchemie von Metallen s. auch
Kap. 3. Strukturchemie von Metallen und Legierungen
aus der Vorlesung Anorganische Strukturchemie
bzw. die Master-Vorlesung Intermetallische Phasen
Auszug Vortrag hierzu (PDF)
Es gibt verschiedene Modelle
zur Beschreibung der Bindung in Metallen und Legierungen:
- Zur Erklärung vieler physikalischer Eigenschaften ist bereits das
Elektronengasmodell nach Drude und Lorentz aus dem Jahr
1900 ausreichend.
Hiernach befinden sich zwischen den positive geladenen Atomrümpfen die freien
Valenzelektronen. Diese verhalten sich wie ein ideales Elektronengas, folgen also
der Boltzmann-Statistik. Der 'Zusammenhalt' des Metalls wird nach diesem Modell durch die elektrostatische
Anziehung zwischen Rümpfen und Elektronen erreicht.
Das Modell ist ausreichend zur qualitativen Erklärung
- der Strukturen (dichte Packung, ungerichtete Bindung),
- der Tatsache, dass die Elektronendichte zwischen den Kernen nicht verschwindet,
- der elektronischen Leitfähigkeit,
- der Wärmeleitfähigkeit,
- der Duktilität und
- der Undurchsichtigkeit (freie Elektronen können Licht aller
Wellenlängen absorbieren).
Das Elektronengasmodell liefert jedoch falsche Sachverhalte für
das thermodynamische Verhalten von Metallen. Beispielsweise ist die
Wärmekapazität cp bei Metallen etwa konstant
über die Temperatur bei einem Wert von 3*R, der Beitrag der
Elektronen ist vernachlässigbar.
Auch der temperaturunabhängige schwache Paramagnetismus (Pauli-Paramagnetismus)
von nicht ferromagnetischen Metallen ist mit diesem Modell nicht erklärbar.
- Beim quantenmechanischen Modell
werden die Elektronen im Unterschied zum
Elektronengasmodell quantenmechanisch als Fermionen, d.h. mit Spin 1/2 und der Fermi-Dirac-Statistik,
behandelt.
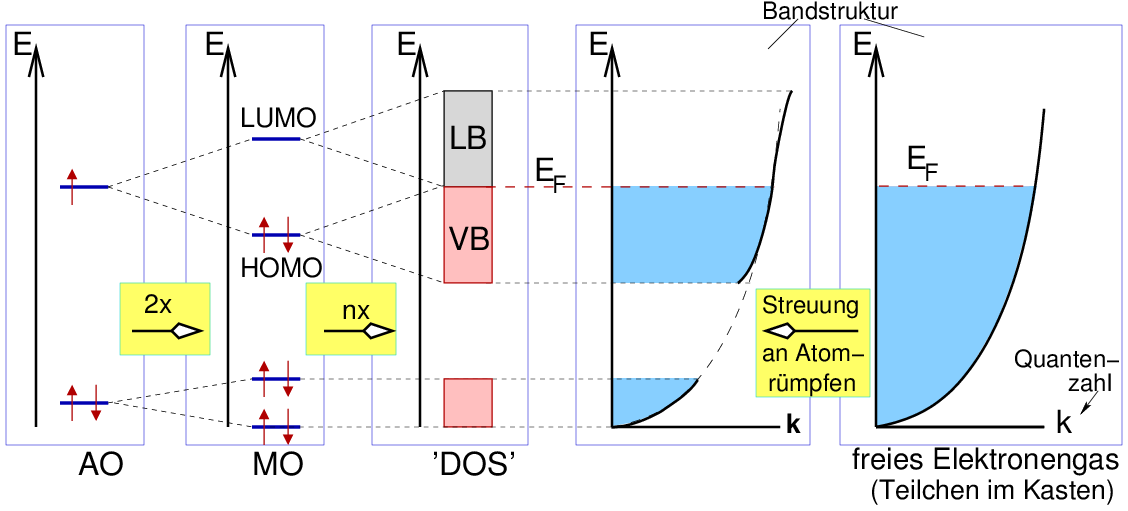
Sehr stark vereinfacht kann ein reales Metall zwischen
dem Grenzfall 'viele Elektronen im potentialfreien Kasten' (rechts) und der Bindung
in Molekülen (MO-Modell, links) beschrieben werden (s. Abb. 1.3.2.):
- Betrachtet man die Abbildung 1.3.2. von links, so erfolgt nach dem MO-Modell
die Linearkombination von Atomorbitalen zu Molekülorbitalen. Werden sehr
viele Atomorbitale (gesamter Metallkristall) kombiniert, dann werden die
Molekülorbitale wegen der Regeln der Quantenmechanik energetisch unterschiedlich,
es entstehen annähernd kontinuierliche Bereiche elektronischer Zustände.
Den höchsten noch mit Elektronen gefüllten Bereich aufgespaltener Zustände nennt
man Valenzband (=HOMO in der Molekülchemie), den niedrigsten, gerade noch nicht
besetzten Energiebereich Leitungsband (=LUMO in der Molekülchemie).
- Auf der rechten Seite der Abbildung 1.4.2. ist die Lösung (Energie in Abhängigkeit
der Quantenzahl k) für das Elektron im Kasten dargestellt. E nimmt quadratisch mit k
zu. Durch Streuung die Elektronen an den positiven Kernen, die im einfachsten Modell
(ganz rechts) vernachlässigt wurden, kommt es zur Bildung von verbotenen Bereichen
in der Energie, so dass letztlich ein ähnliches Bild resultiert wie nach dem MO-Modell.
- Für die elektronischen Eigenschaften (Leitfähigkeit) und den Pauli-Paramagnetismus
der Metalle sind wesentlich nur die energiereichen Elektronen des obersten Bereichs
des Valenzbandes verantwortlich. Auch bei Temperaturerhöhung ändert sich
die Energie dieser Elektronen nur minimal, was z.B. den geringen Anteil der Elektronen
an der Wärmekapazität erklärt.
- Weitere Details zu diesen Bindungsmodellen finden sich im
beim M+K-Kurs Quantenchemische Rechenmethoden (hier PDF zum
Kapitel V: Bandstruktur und Eigenschaften) sowie im
Kap. 2.2. Elektronische Strukturchemie von Metallen
aus der Vorlesung Intermetallische Phasen.
Aufgrund der Zustandsdichten (manchmal auch falsch als 'Bandstrukturen' bezeichnet,
richtiger DOS = Density of States = Zustandsdichte)
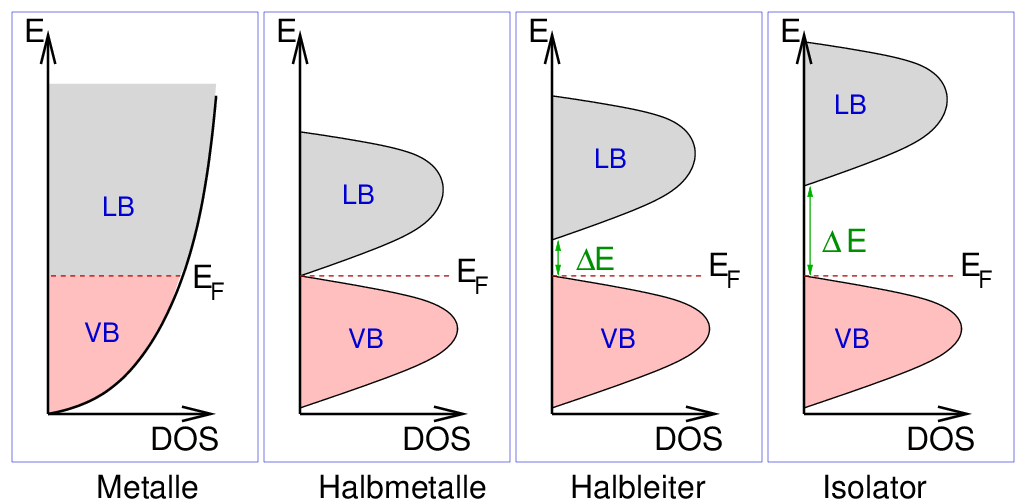
können daher die Feststoffe eingeteilt werden in (s. Abb. 1.3.3.):
- Metall: überlappende (z.B. Ca) oder teilbesetzte (z.B. Na) Bänder
- Halbmetall: wie Metalle, aber mit geringer Zustandsdichte am Ferminiveau (schlechte Metalle)
- Halbleiter: schmale (ca. 1-2 eV) verbotene Zone zwischen Valenzband und Leitungsband
- Isolator: große verbotene Zone zwischen besetztem Valenz- und leerem Leitungsband
Die Übergänge zwischen Metall und Halbmetall sowie zwischen
Halbleiter und Isolator sind natürlich fliessend, diese beiden
Gruppen selber unterscheiden sich wie im Kapitel 1.2. besprochen
grundlegend in der Temperaturabhängigkeit der elektronischen Leitfähigkeit.