1.2. Chemische Bindung, Strukturkonzepte

1.2.1. Die Natur der Si-O-Bindung

Der Vergleich der Verbindungsbildung von Silicium und seinem leichteren Homolgen, dem Kohlenstoff, mit Nichtmetallen zeigt, dass aufgrund der Bindungsenergien beim Kohlenstoff C-C bzw. C-H-Bindungen, beim Silicium dagegen die Si-O- Bindungen bevorzugt sind.

In der Strukturen der Silicate treten als Koordinationszahlen von Silicium meist 4, weniger häufig auch 6 auf. Dominierend ist die tetraedrische Koordinationssphäre, die einem sp³-Hybrid (mit Anteilen von π-π-Bindungen zwischen O-p und Si-p sowie sehr begrenzt auch Si-d-Zuständen, s.u.) entspricht. Charakteristisch für diese Koordinationszahl ist ein Abstand d_Si-O von 162 pm. Seltener findet sich auch die Koordinationszahl 6, d.h. oktaederische Umgebung (Hypervalenz wie bei SF₆) mit einem typischen Abstand d_Si-O von 177 pm (Druck-Abstands-Paradoxon!). Diese Koordination wird bei Si-O-Hochdruckphasen, bei Si-Phosphat, einigen Si-Komplexen (z.B. mit Brenzcatechin als Ligand) und in SiF₆^2- (d.h. mit stark elektronegativen Liganden) beobachtet.
Aufgrund der generellen Strukturprinzipien, der Verknüpfung von SiO₄-Tetraedern über unterschiedlich viele Ecken, ist Sauerstoff in Silicaten entweder von zwei (brückend) oder nur von einem (endständig/terminal) Si-Atom koordiniert.

Für den Bindungscharakter der Si-O-Bindung (ionische Formulierung entsprechend Si⁴⁺ und O^2- versus kovalente Formulierung) ergibt sich nach Pauling z.B. für Quarz ein Ionencharakter 1-e^{1/4(χ_A-χ_B)} von 15 %.
Für den Si-O-Abstand in Silicaten ergibt sich

bei Annahme einer rein ionischen Bindung aus der Summe der Ionenradien nach Shannon ein Wert von 176 pm (r(O^2-) = 140 pm und r(Si⁴⁺) = 36 pm).
Die berechne Si-O-Bindungslänge, die sich bei Annahme rein kovalenter Bindung aus der Summe der Kovalenzradien von 66 pm für O und 117 pm für Si ergeben, beträgt sogar 183 pm.
Beobachtet wird jedoch in Silicaten ein Wert von ca. 162 pm, d.h ein geringerer Wert als nach allen Konzepten berechnet.

Diese kurzen Bindungsabstände d_Si-O sind nur durch erheblicher Doppelbindungsanteile zu erklären (s.u.).

Innerhalb der Silicate variieren die Si-O-Abstände zwar nicht sehr stark, es gibt jedoch eindeutige Tendenzen: Bereits Gibbs und Brown (1969) haben eine Korrelation zwischen der Koordinationszahl von Sauerstoff (berechnet mit Si und allen weiteren A-Kationen) und der Si-O-Bindungslänge festgestellt, die in Abb. 1.2.1 dargestellt ist: Danach steigt der Si-O-Abstand mit der Koordinationszahl von Sauerstoff, in SiO₂ ist der Abstand kürzer als z.B. in Orthosilicaten, wo die O-Atome hohe Gesamt-Koordinationszahlen aufweisen.

Abb. 1.2.1. Korrelation des mittleren Si-O-Abstands mit der Gesamtkoordinationszahl von Sauerstoff (nach Brown und Gibbs) ‣SVG
Betrachtet man lediglich die Koordination von O gegen Si, wird ebenfalls eine klare Tendenz deutlich: Terminale (CN_O=1) Si-O-Abstände sind stets etwas kürzer als Abstände zu verbrückenden Sauerstoffatomen.
Der beobachtete Bindungswinkel am Sauerstoff liegt im Durchschnitt bei 140 ^o, wobei der Bereich zwischen ca. 110 und 180^o schwankt. Dabei ist allerdings zu beachten, dass die zumeist röntgenographisch ermittelten Si-O-Si-Winkel in nicht wenigen Fällen durch die speziellen Lagen der Sauerstoffatome verfälscht sind! Als Erklärung für diese gegenüber dem Tetraederwinkel deutlich aufgeweiteten O-Si-O-Winkel kann wiederum der Doppelbindungsanteil der Si-O-Bindung herangezogen werden.

Die Diskussion der elektronischen Struktur von Oxido-Orthoanionen (Orthosilicat [SiO₄]^4- aber auch Phosphat, Sulfat, Perchlorat usw.) auf der Basis aktueller theoretischer Rechnungen ergibt inzwischen ein einigermassen sicheres Bild, obwohl abhängig vom Rechenverfahren weiter über die Anteile von π-π-Bindungen zwischen O-p und Si-p bzw. 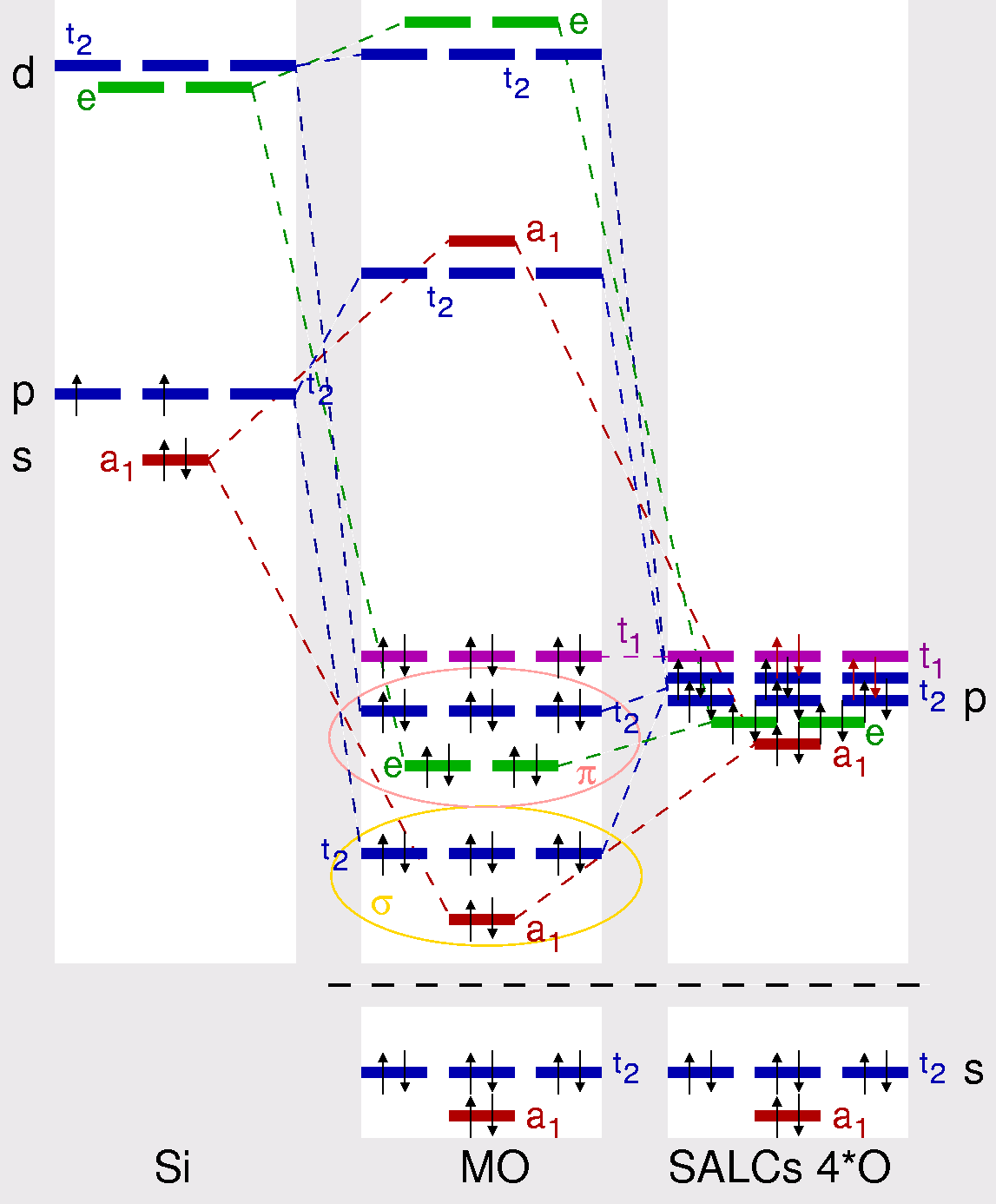Si-d-Zuständen diskutiert wird (der sich auch auf die 'erlaubten' Schreibweisen für die Valenzstrichformeln der Anionen auswirkt). Hierzu ist in Abbildung 1.2.2. schematisch das MO-Schema des Orthosilicat-Ions wiedergegeben.

Abb. 1.2.2. Schematisches MO-Schema des Orthosilicat-Ions ‣SVG
Die beteiligten Atomorbitale des zentralen Si-Atoms sind Si-s (a₁, in rot) und Si-p (t₂, in blau) Zustände, die mit vier Elektronen besetzt sind. Die d-Orbitale bilden im Tetraeder einen e (d_z²- und d_x²-y²-Orbitale, in grün) und einen (t₂, in blau) Orbitalsatz. Die s-Orbitale der vier Sauerstoff-Liganden kombinieren zu einem totalsymmetrischen a₁ und einem t₂-Satz. Diese Orbitale liegen energetisch so tief, dass sie nicht an der Bindung beteiligt sind (hohe s-p-Separation bei O). Die 12 p-Orbitale der vier O-Atome, die mit 20 Elektronen (4+4 = 16 + 4 für die Ladung) besetzt sind, bilden SALCs der irreduziblen Darstellungen a₁, e, t₁ und 2 x t₂.
Die daraus entstehenden Molekülorbitale des Anions sind:

Die tiefliegenden a₁- und t₂-Sätze der O-s Zustände sind nichtbindend (8 Elektronen).
Die a₁- und t₂-Molekülorbitale (aus O-p und Si-s/p-AO) bilden die σ-Bindung zwischen Si und O (8 Elektronen).
Die e- und t₂-Molekülorbitale entstehen durch Linearkombinationen der O-p-Zustäde (Hauptanteile) und Si-p- (t₂, in blau) bzw. Si-d-Atomorbitale (geringe Anteile). Die Absenkung dieser beiden Molekülorbitale gegenüber den SALCs der O-Liganden rechts representieren die π-Anteile der Si-O-Bindung.
Der nichtbindende Orbitalsatz t₁ aus O-p-SALCs bildet den höchsten besetzten Zustand (6 Elektronen).

Selbstverständlich kann ein solches lokales Molekülorbital-Modell (alleine schon wegen der erheblichen Ladung, praktisch nicht zu berechnen!) die Bindungsverhältnisse in einem Festkörper nicht korrekt wiedergeben.

Die Ergebnisse eine DFT-Bandstruktur-Berechnung (vollrelativitsiche FP-LAPW-Methode) von BaSiO₃ (ein synthetisches Kettensilicat) zeigen die erheblichen Si-d-Anteile (grau unterlegt) unterhalb des Fermi-Niveaus jedoch ebenfalls sehr deutlich (s. tDOS (oben) sowie pDOS von Si und O (unten) in Abbildung 1.2.3.).

Abb. 1.2.3. Totale und partielle Zustandsdichten in BaSiO₃ ‣SVG
Die Abbildung der Elektronendichte aus dieser Rechnung (Abb. 1.2.4.) zeigt, dass der bindungskritische Punkt (Sattelpunkt der Elektronendichte) sehr nahe am Silicium liegt und der Wert für die Elektronendichte an dieser Stelle nur sehr gering ist, der ionische Bindungsanteil ist nach dieser Rechnung sehr deutlich.

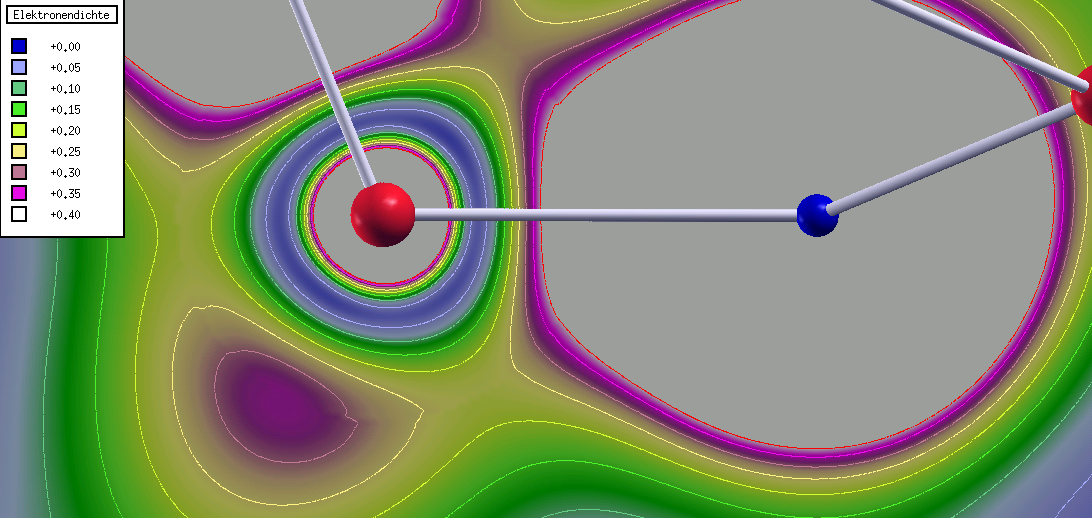Abb. 1.2.4. Valenzelektronendichte in BaSiO₃

1.2.2. Kationen außer Si, Wasser

Die wichtigsten Kationen in Silicaten und deren übliche Koordinationszahlen (CN) gegenüber Sauerstoff sind in Tabelle 1.2.1 zusammengestellt.

Kation	CN gegen O
Be²⁺	4
Li⁺	4, (6)
Al³⁺	4,6
Mg²⁺	(4), 6
Fe²⁺, Ti⁴⁺	6
Na⁺, Ca²⁺	6, (8)
K⁺	6-12

Tab. 1.2.1. Kationen in Silicaten
Danach können die Kationen von Be²⁺, Li⁺ und Al³⁺ Silicium auf den Tetraederplätzen ersetzen (sog. isomorpher Ersatz). Aluminium kommt eine doppelte Rolle zu, es fungiert entweder als 'echtes Kation' (Aluminium-Silicat) oder es ersetzt Silicium auf seinen Plätzen (Alumo-Silicat). Diese Doppelrolle von Al erschwert die Interpretation von Formeln der entsprechenden Si/Al-Verbindungen. Die Kationen üben auf die Si-O-Bindung einen induktiven Effekt aus, d.h. die Kationen verstärken als Elektronen-Donatoren den Si-O-Doppelbindungscharakter. Dadurch werden die Brückenbindungen länger (Mittelwert: 163 pm), endständige (terminale) Si-O-Si-Bindungen werden dagegen - entsprechend einem stärkerer Doppelbindungsanteil - kürzer (Mittelwert: 158 pm). Die folgende empirische Regel beschreibt die entsprechende Bindungslängenvariation:
d_Si-O = 157.9 + 0.15 * CN_O

Wasser ist in Silicaten fast immer als echtes Kristallwasser eingebaut. Es sind nur wenige Hydroxy-Silicate mit [SiO_x(OH)_y]-Tetraedern bekannt. Auch diese Tatsache erleichtert das Verständnis der Struktuchemie (hydratisierter) Silicate sehr erheblich.

1.2.3. Strukturkonzepte, Pauling-Regeln

Aufgrund des relativ hohen ionischen Bindungsanteils können die Strukturen der Silicate A_x[Si_yO_z] auch häufig als Ionenkristalle aus O^2--Anionen und Si⁴⁺- und Aⁿ⁺-Kationen beschrieben werden (Konzept der Kondensation von Kationenkoordinationspolyedern, KKPs). In diesem Fall gelten die Pauling-Regeln für Ionenkristalle, die vereinfacht die Minimierung der potentiellen Energie in Ionenkristallen wiedergeben. Die Pauling-Regeln gelten für Silicate fast immer. (s. zu den Pauling-Regeln auch Kap. 4.2. der Vorlesung Anorganische Strukturchemie).

Radienverhältnisregel: Die Koordinationszahl wird in Ionenkristalle vom Verhältnis der Radien der beteiligten Ionen bestimmt. Die Abstände selber folgen der Summe der Ionenradien. Genauer: Nach Einführung von Polyedern um die Kationen (Festlegung der Koordinationszahl) und bei Zuordnung von Ionenradien zu den einzelnen Teilchen wird die Koordinationszahl (CN) vom Radienverhältnis, die Atomabstände vom Wert der Ionenradien bestimmt.

Um jedes Kation wird ein Koordinationspolyeder gebildet. Der Abstand zwischen Kation und Anion ist durch die Summe der Ionenradien bestimmt, die Koordinationszahl dagegen vom Radienverhältnis.

Beispiele: Bekanntestes Beispiel ist die Strukturtypenfolge (ZnS, NaCl, CsCl) bei einfachen Salzen. Bei Silicaten ergibt sich aufgrund der Ionenradien von Si⁴⁺ und O^2- unmittelbar die Koordinationszahl 4 für Silicium gegen Sauerstoff. Die Werte für andere Kationen entsprechen den in der Tabelle 1.2.1 oben angegebenen und sind graphisch in Abb. 1.2.5. dargestellt.

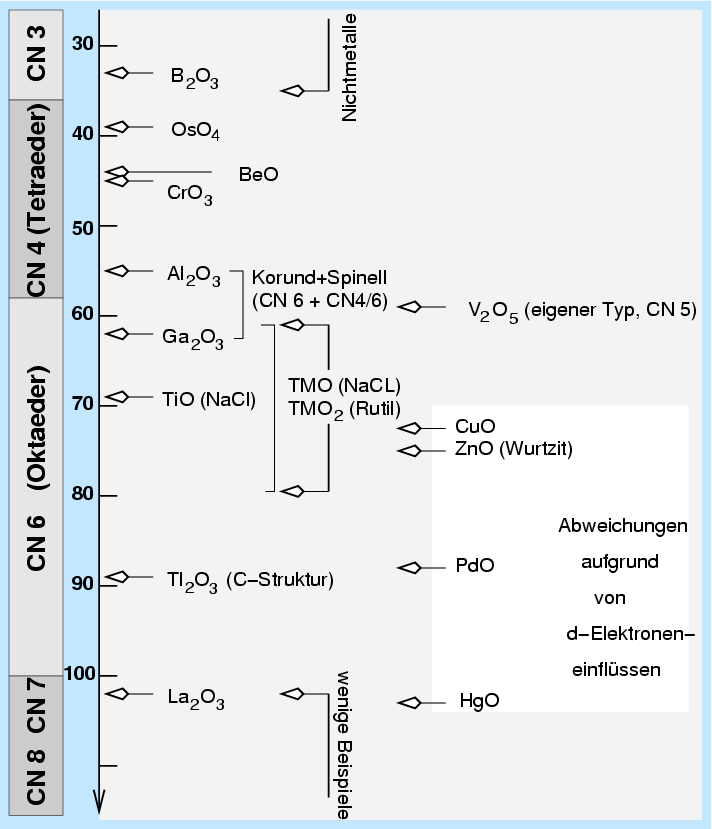Abb. 1.2.5. Radienverhätnis-Regel und typische Kationenkoordinationen ‣SVG
Sind in einer Verbindung unterschiedliche Kationen vorhanden, dann können eventuell nicht alle ideale Verhältnisse finden. In diesem Fall weichen die Kationen mit der geringsten Ladung und dem größten Radius auf andere Koordinationszahlen aus. Beispielsweise liegt Natrium im Sodalith Na₈[Si₆Al₆O₂₄]Cl₂ nicht wie sonst mit der Koordinationszahl 6, sondern nur mit einer Koordinationszahl von 4 vor, während Si (höhere Ladung!) in CN 4 verbleibt.
Elektrostatische Valenzsummenregel: Für jedes Kation i mit der Ladung Z und der Koordinationszahl CN ergibt sich die 'elektrostatische Bindungsstärke' S_i zu: S_i=^{(Z e)}/_CN Ein stabiles Ionengitter liegt dann vor, wenn die Ladung X e der Anionen der Summe der Bindungsstärken der koordinierenden Kationen entspricht: X = Σ_i s_i Die Summation erfolgt über die i-Kationen um das jeweilige Anion.
Oder als Text:

Die Valenz eines Anions in einer stabilen ionischen Struktur versucht die Stärke der elektrostatischen Bindungen der umgebenden Kationen zu kompensieren (und umgekehrt).

Beispiele:
1. Perowskit CaTiO₃:
  Für die einzelen Kationen gilt:
  - Ca: Z = +2; CN=12, d.h. ^Z/_CN = ¹/₆
  - Ti: Z = +4; CN=6 d.h. ^Z/_CN = ²/₃
  Da Sauerstoff (Z = -2) von zwei Ti- und vier Ca-Atomen koordinert ist, gilt S = 4 * ¹/₆ + 2 * ²/₃ = 2. D.h. also, dass die Ladung des O^2- genau ausgeglichen wird.
2. Spinell: MgAl₂O₄
  Für die Kationen gilt wieder:
  - Mg: Z = +2; CN=4, d.h. ^Z/_CN = ¹/₂
  - Al: Z = +3; CN=6, d.h. ^Z/_CN = ¹/₂
  Da Sauerstoff von einem Mg- und drei Aluminium-Ionen koordiniert ist, wird auch hier die Ladung von O^2- ausgeglichen ( (1+3) * ¹/₂ = 2)
3. Granate (A₃²⁺B₂³⁺[SiO₄]₃):
  Aufgrund der Koordinationszahlen ergeben für die Kationen (am Beispiel Grossular):
  - Ca (A): Z = +2; CN=8, d.h. ^Z/_CN = ¹/₄
  - Al (B): Z = +3; CN=6, d.h. ^Z/_CN = ¹/₂
  - Si: Z = +4; CN=4, d.h. ^Z/_CN = ¹/₁
  Da die Oxid-Ionen von zwei Ca-, einem Al- und einem Si-Kation umgeben ist folgt für diese Anionen: 2 * ¹/₄ + 1 * ¹/₂ + 1 * 1 = 2 (q.e.d.)
4. Bei den Silicaten (weitere Rechnungen folgen bei einigen Strukturen) gibt es maximale Abweichungen von der elektrostatischen Valenzregel von nur ¹/₆. Diese Regel kann bei Silicaten für die Bestimmung der Al-Positionen in Alumosilicaten herangezogen werden. Ferner dient sie zur Unterscheidung von O^2-, OH^- und H₂O-Positionen sowie zur Bestimmung der Oxidationszustände von Ionen (z.B. Fe^2+/3+).

3. Pauling-Regel: Bei Salzen mit mehreren Kationen werden diejenigen mit hoher Ladung möglichst weit voneinander weg eingebaut, so dass eine möglichst gute Abschirmung der Kationen voneinander möglich wird. D.h., dass die Kationen-Koordinationspolyeder möglichst wenige Polyederelemente gemeinsam haben sollten.

Oder als Text:

Teilung von Kanten und besonders von Flächen zwischen Koordinationspolyedern reduziert die Stabilität einer Struktur. Dieser Effekt ist besonders ausgeprägt für Kationen hoher Valenz und geringer Koordinationszahl.

Beispiele:

Bei Silicaten sind keine Beispiele für gemeinsame Flächen zwischen Tetraedern und keine Beispiele für gemeinsame Kanten zwischen Tetraedern bekannt. Die SiO₄-Tetraeder sind stets entweder isoliert oder über gemeinsame Ecken miteinander verknüpft.
Der Vergleich der Reihe Silicate [SiO₄]^4- -> Phosphate [PO₄]^3- -> Sulfate [SO₄]^2- zeigt, dass wegen der in dieser Reihe steigenden Ladung des Kations Phosphate meist nur mit wenigen gemeinsamen Ecken auftreten (häufig isoliert, als Dimere oder maximal Ketten) und dass bei Sulfaten keinerlei Tendenz zur Kondensation der [SO₄]-Tetraeder zu beobachten ist.

Als Erweiterung der 3. Pauling-Regel gilt, dass mehrere Kationen hoher Ladung räumlich weit voneinander getrennt sein sollten, d.h. dass diese möglichst wenige Polyederelemente gemeinsam haben sollten.

Oder im Text

In einer Struktur mit mehreren Kationen weichen Kationen mit hohen Ladungen einem Teilen von Bauelementen aus.

Die Konsequenz für Alumosilicate ist die sogenannte Löwenstein-Regel, nach der niemals zwei Aluminium-Atome nebeneinander in den Tetraederverband eingebaut sind.

'Sparsamkeitsregel': Insgesamt werden möglichst wenige Koordinationen realisiert.
Im Text:

Die Zahl verschiedener Bauelemente in einer Kristallstruktur ist klein.

Allgemein ergibt sich, dass 3-dimensionale Verbände stabiler sind als zweidimensionale und diese wiederum stabiler als isolierte Baugruppen.

Wie bei anderen Ionenkristallen auch ist häufig statt des Konzeptes der KKPs auch eine Betrachtung als dichten Packungen der Anionen (Oxid-Ionen), in der die Si- und A-Kationen die Tetraeder- und Oktaederlücken besetzen, sehr nützlich. Dies gilt insbesondere für Verbindungen wie z.B. die Orthosilicate, bei der die kovalente Beschreibung über unterschiedlich kondensierte SiO₄-Tetraeder nicht greift.

<<<< Inhalt Kap. 1 Kap. 2 Kap. 3 Kap. 4 Kap. 5 Kap. 6 Kap. 7 Kap. 8 Kap. 9 >>>>

cr_home Nichtmetalle (ACI) Metalle (ACII) FK-Chemie (ACV) Methoden (ACIV) Strukturchemie Interm. Phasen Oxide Strukturtypen